АНАЛИЗ И ПРОЕКТИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ (часть 2)

Абросимов  Л. И.

 

2. МЕТОД КОНТУРОВ ДЛЯ ОЦЕНКИ ПРОИЗВОДИТЕЛЬНОСТИ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ

 

2.1. Основные положения и определения

Вычислительные сети характеризуются большой сложностью составляющих элементов, связей, взаимодействий, параметров и характеристик. При построении моделей основное внимание уделяется тем характеристикам и параметрам, которые интересуют исследователя - проектировщика.

К основным понятиям рассматриваемой модели относятся структура и составляющие ее компоненты.

Под структурой модели вычислительной сети понимаются условия и средства соединения компонентов сети ( рис.2).

 

Компонентами моделируемых вычислительных сетей обычно являются узлы сетей и каналы передачи данных, соединяющих компоненты.

Узел моделируемой сети — это аппаратные и программные средства файл-сервера, хостмашины, коммуникационного контроллера, терминала (см. рис. 2). Каждый узел при обработке осуществляет задержку сообщений и поэтому моделируется одноканальной системой массового обслуживания M/M/1/ (рис. 3).

 

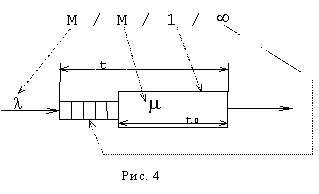
Основными параметрами сообщений являются: интенсивность  поступления  сообщений и интенсивность обслуживания  сообщений в узле.

Интенсивность поступления  сообщений равна усредненному количеству сообщений, поступающих на вход узла в единицу времени.

Интенсивность обслуживания  сообщений в узле равна усредненному количеству сообщений, обслуженных в единицу времени.

Основными характеристиками узлов, как систем массового обслуживания являются:

время обслуживания   сообщений узлом, где
(1)

время задержки t сообщений в системе  i (в узле и очереди на обслуживание) :
(2)

коэффициент загрузки 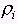узла i:
(3)

количество сообщений   в системе обслуживания (в узле и очереди на обслуживание)
(4)

количество сообщений  в очереди на обслуживание:
(5)

Рассматриваемая модель учитывает стационарный, установившийся процесс передачи и обслуживания заявок. Если обслуживающая система содержит несколько узлов с явно выраженными входом и выходом, то такая система называется открытой системой, а интенсивность входящих сообщений равна интенсивности выходящих сообщений. (см. рис.4).

Количество сообщений в открытой системе определяется по формуле Литтла (6).

Если обслуживающая система содержит несколько узлов, а поток сообщений с выхода последнего узла поступает на вход первого узла , то такая система называется замкнутой системой, а интенсивность потока сообщений является неизвестной величиной, зависящей от параметров  и структуры соединения узлов. (рис. 6 )

 

 

Для замкнутой системы применение формул (4, 5), выведенных для одноканальной системой массового обслуживания M/M/1/, приводит при небольших количествах сообщений (n= 1 — 10) к значительным погрешностям. Для уменьшения погрешности при расчете характеристик замкнутых систем необходимо использовать коэффициент  ограниченности очереди:

 = ( —)/;   где   = 0 |;       = 1|.

Тогда соотношения (4, 5) преобразуются к следующему виду:

количество сообщений   в замкнутой системе обслуживания (в узле и в очереди на обслуживание):
(6)

количество сообщений  в очереди на обслуживание к узлу i в замкнутой системе обслуживания:
(7)

В вычислительных сетях можно выделить потоки сообщений, каждый из которых в установившемся режиме имеет свой путь прохождения через узлы сети и свои параметры обслуживания в узлах. Такой условно выделенный путь движения сообщений назван контуром , где . Контуры могут быть разомкнутыми (см. рис. 5, 8) и замкнутыми (см. рис.6, 7).

 

Разомкнутый контур — это путь потока идентичных сообщений от входа в сеть через промежуточные узлы к выходу из сети.

Замкнутый контур — это путь потока идентичных сообщений от узла-источника до обслуживающего узла и обратно.

Фаза контура — это часть контура, в которой каждый узел только один раз обслуживает сообщение.

Пример 2.1 (см. рис 7) : замкнутый контур содержит узлы: (A)¾k1¾k2¾k3¾(B)¾k2¾(A).

Пример 2.2 (рис 7) : Фаза =1 содержит узлы: (A)¾k1¾k2¾k3¾(B). Фаза  = 2  содержит узлы: (B)¾k2¾(A).

 


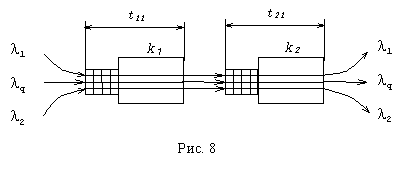
В реальных сетях в стационарном режиме сообщения с выхода одного узла могут поступать на входы различных узлов. При моделировании такие переходы от узла ki к узлу kj оцениваются вероятностью  перехода сообщений (см. рис 9).

 

 

Вероятности  перехода позволяют для разомкнутых контуров выразить интенсивность  потока сообщений  любого перехода через базовую интенсивность потока сообщений и коэффициент  базовой интенсивности. Базовую интенсивность потока сообщений обычно представляет поток сообщений, поступающий на вход узла. Коэффициент  базисной интенсивности, показывает, какая часть базисной интенсивности переходит от узла ki к узлу kj, т.е.:
(8)

Пример 2.3 (см. рис 9):

 a12 = p12 ;  a13 = p13 ;  a24 = p12× p24 = p12 ;

a34 = = p13× p34 ;   a35 = p13× p35;  

a45 = (a24 + a34)p45 = a24 + a34.

 

2.2. Линейные уравнения

 

Линейные уравнения являются одной из составных частей аналитической модели метода контуров. Составление и последующее их совместное решение позволяет для потоков каждого контура q определить коэффициенты  базовой интенсивности.

В основу составления линейного уравнения положено условие, что для установившегося процесса движения сообщений одного контура  количество входящих в узел ki сообщений равно количеству сообщений его покидающих и поступающих на вход следующего узла kj (рис 10).

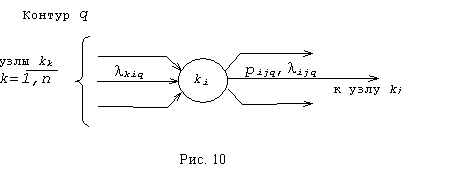
Тогда для каждого контура , каждого узла  и для каждой дуги можно записать:
(9)

Пример 2.4. (см. рис. 9):

 Система линейных уравнений имеет вид:

 = ;     = ;     = ;  

= ;     = ;      = ( + ).

Решая системы линейных уравнений, получаем:

 = ;      = ;    = ;      = ;  = ;    =  +

 

2.3. Нелинейные уравнения

 

Нелинейные уравнения также являются частью аналитической модели метода контуров. Каждое нелинейное уравнение составляется для одного контура. Составление и последующее их совместное решение позволяет для потоков всех контуров сети определить базовые интенсивности.  . Основу составления каждого нелинейного уравнения составляет условие, что для установившегося процесса движения сообщений одного контура  количество сообщений в контуре не изменяется и равно сумме математических ожиданий сообщений рассматриваемого контура во всех узлах сети.  Тогда для каждого контура можно записать:
(10)

 

 

Пример 2.5 (см.рис.11):

Рассматриваемая система содержит два замкнутых контура.

 

контур  q = 1 содержит в своем составе узлы: k1¾k3¾k4¾k3¾(k1 ; первая фаза  = 1 содержит узлы k1—k3—k4 ; вторая фаза  = 2 содержит узел  k3 . контур  q= 2 содержит в своем составе узлы: k2¾k3¾k4¾k3¾(k2 ; первая фаза  = 1 содержит узлы k2—k3—k4..; вторая фаза  = 2 содержит узел  k3.

Система нелинейных уравнений для рис. 11 на основании (6) и (10) может быть записана в следующем виде:

 

                            (11)

 

где             .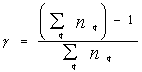

 

2.4. Решение нелинейных уравнений

 

Целью решения системы нелинейных уравнений является вычисление базисных интенсивностей  для каждого контура . В качестве базисной обычно выбирается дуга контура , выходящая из узла ki с наименьшим номером i.

Анализ соотношений (6) и (10) показывает, что каждое нелинейное уравнение  в области допустимых решений представляет собой монотонно возрастающую функцию. Вид зависимости () для первого нелинейного уравнения примера 2.5 представлен на рис 12.

 

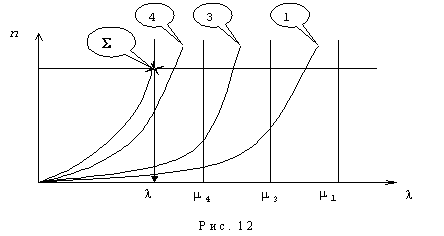
На рис. 12 номера "1", "3", "4" — соответствуют номерам узлов первого контура, которые описываются слагаемыми в соотношении (11). Знаком обозначена вся правая часть первого нелинейного уравнения.

Для решения системы нелинейных уравнений используем  итеративный метод дихотомии, называемый также "метод проб" [9].

Для этого представим соотношение (10) в канонической форме:
(12)

Каноническая форма нелинейного уравнения (12) изображена на рис 13.

Решению уравнения соответствует равенство: () = 0.

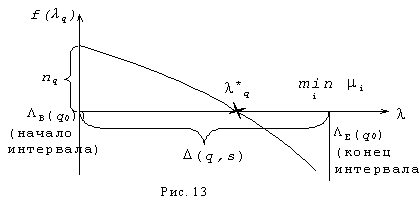
В основу процедуры решения нелинейного уравнения положены следующие условия:

1) если корень уравнения лежит между  =    и  = , то вычисляют  {( + )/2};

2) если {(+)/2}.имеет тот же знак, что и (), то присваивают  = ( + )/2 , а  не изменяют и повторяют процедуру вычисления ();

3) если {(+)/2} имеет тот же знак, что и (), то присваивают  = ( + )/2 , а  не изменяют и повторяют процедуру вычисления ();

4) расчет продолжается до тех пор, пока на шаге  будет достигнуто условие:

 = |( ) — ()| /( )  < , где

 — заданная точность вычислений.

Ответственным является шаг  = 0, на котором назначаются значения граничных  величин:  и .

Для рассматриваемого типа нелинейных уравнений  для каждого контура  целесообразно принимать:

Пример 2.6. (см. рис. 10): для контура  = 1,  n1=3;  m1=1  1/s;

m3=4  1/s; m4=3 1/s , );  

для контура  = 2  n2=4;  m2=2 1/s; m3=4 1/s; m4=3 1/s (точность вычислений  = 6%).

По соотношению (11) вычисляем :

                g1=0,67; g2=0,75; g3=0,86; g4=0,86  .

Последовательно для каждого контура  и каждого шага  вычисляем:  (q,s),    (q,s),  f(q,s),  (s):

s=0         LB(1,0)=0; LE(1,0)=1;          LB(2,0)=0; LE(2,0)=2 ;

s=1         l1(1)=0,5; l2(1)=1; f(1,1)=1,26; f(2,1)=1,22 ;

LB(1,1)=0,5; LE(1,1)=1; LB(2,1)=1; LE(2,1)=2 ;

s=2         l1(2)=0,75; l2(2)=1,5; f(1,2)= -10,75; f(2,2)= -22,2;

LB(1,2)=0,5; LE(1,2)=0,75; LB(2,2)=1; LE(2,2)=1,5;

s=3         l1(3)=0,62; l2(3)=1,25; f(1,3)=-0,09; f(2,3)=-0,94;

                LB(1,3)=0,5; LE(1,3)=0,62; LB(2,3)=1,0; LE(2,3)=1,25;

s=4         l1(4)=0,56; l2(4)=1,13; f(1,4)=0,72; f(2,4)=0,22;

                LB(1,4)=0,56; LE(1,4)=0,62; LB(2,4)=1,13; LE(2,4)=1,25.

С заданной точностью  = 6%  получаем,

 l1 = 0,59 1/s, l2 = 1,19 1/s.

 

2.5. Определение функциональных характеристик

Каждый узел  вычислительной сети характеризуется временем   обслуживания сообщений, которое зависит от объема заданий и производительности   узла:
(13)

Если узел моделирует компьютер, то объем  заданий измеряется в операциях, а производительность узла измеряется в операциях в секунду. Если узел моделирует аппаратуру связи, то объем заданий измеряется в битах, а производительность узла измеряется в битах в секунду.

После того, как определены интенсивности  потоков сообщений каждого контура  в каждом узле ki вычислительной сети можно определить основные характеристики вычислительной сети.

Среднее время  доставки сообщений контура  в разомкнутой сети:
(14)

Среднее время отклика  сообщений замкнутого контура , содержащего  сообщений, каждое из которых генерируется узлом ki :
(15)

Коэффициент  загрузки узла i:
(16)

 

2.6. Стадии метода контуров

Изложенные основные определения позволяют сформулировать следующие этапы метода контуров:

- описание структуры вычислительной сети,

- описание функциональной схемы вычислительной сети,

- представление графовой модели вычислительной сети,

- составление линейных уравнений баланса,

- составление нелинейных уравнений баланса,

- решение линейных уравнений баланса,

- решение нелинейных уравнений баланса,

- определение функциональных характеристик ВС.

Структура вычислительной сети определяет такие основные характеристики, как количество N узлов сети и связи между узлами, как показано на рис.2,  задаваемые матрицей связей // // .

Переход к функциональной схеме вычислительной сети отражает требования проектировщика-исследователя к степени детализации построения модели, т.е. функциональная схема содержит те элементы сети, которые вносят, по-мнению проектировщика существенные задержки времени в обработку сообщений. На этой стадии определяются контуры  и фазы  поступающих на обслуживание потоков сообщений, а также интенсивности  обслуживания сообщений в узлах.

Графовая модель служит для формализорванного представления функциональной модели и позволяет символьно определить все параметры и характеристики для математического описания модели. При наличии  узлов, имеющих идентичные интенсивности  обслуживания вводятся типы  узлов обслуживания.

Составление линейных уравнений баланса выполняется в соответствии с пояснениями, изложенными в параграфе 2.2. и записывается в виде соотношения (9).

Составление нелинейных уравнений баланса выполняется в соответствии пояснениями, изложенными в параграфе 2.3. и записывается в виде соотношения (10).

Решение системы линейных уравнений баланса направлено на определение коэффициентов  базисной интенсивности для чего, в зависимости от размерности сети могут использоваться различные методы решения (подстановки или итеративные методы [9]).

Решение системы нелинейных уравнений баланса ставит своей целью вычисление базисных интенсивностей для замкнутых контуров. Для систем не большой размерности целесообразно использовать метод дихотомии, изложенный в разделе 2.4. Выбор метода решения для сетей большой размерности требует дополнительного анализа специфических особенностей каждой исследуемой сети.

Для определение функциональных характеристик вычислитель-ных сетей используются соотношения параграфа 2.5.

2.7.Упражнения

Контрольные вопросы

1. Какие условия являются главными для рассмотрения компоненты сети в качестве узла?

2. Какие характеристики трафика являются известными (заданными) для замкнутых и разомкнутых контуров?

3. Почему для замкнутых систем обслуживания с узлами M/M/1 и M/G/1 необходимо вводить коэффициент ограниченности очереди? В каком диапазоне он изменяется?

4. Сколько фаз может иметь контур?

5. Почему уравнения (9) называют линейным, а уравнение (10) — нелинейным?

6. Какие итеративные методы решения нелинейных уравнений Вам известны?

Задания

1. Разомкнутая система обслуживания А имеет интенсивность входного потока и время обслуживания . Разомкнутая система обслуживания В состоит из двух последовательно-соединенных узлов и имеет время обслуживания в каждом узле = /2. Для одинаковой интенсивности входного потока  определите, какая система имеет большее время обслуживания? Может ли  быть равным ?

2. Разомкнутая система обслуживания C состоит из двух параллельно соединенных узлов, входной поток сообщений с равными вероятностями поступает на входы каждого узла, который имеет время обслуживания  = . Определите время обслуживания  и сравните с  и (см. Задание 1).

3. Определите время пребывания сообщений в системе       (см.

рис. 5.), если =1, а коэффициенты загрузки===0,8.

4. Определите время пребывания сообщений в системе       (см.

рис. 8 ), если =1, =2, =3, =7, =8. Определите коэффициенты загрузкии . Какое получится решение при =6 и почему?

5. Определите интенсивность потоков для системы, представленной на рис. 11, если она обслуживает:

а) только контур q1, 

б) только контур q2.

Сравните результаты решения этой задачи с примерами 2.5 и 2.6.