АНАЛИЗ И ПРОЕКТИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ (часть 4)

Абросимов  Л. И.

 

4. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК Ring-LAN

 

4.1. Постановка задачи

В процессе проектирования кольцевой сети (Ring-LAN) разработчики задают различные структуры вычислительных сетей, а также возможные направления информационных потоков и для этих вариантов определяют временные характеристики, чтобы сделать оценку каждого варианта функционирования Ring-LAN.

Решаемая в настоящей главе задача формулируется следующим образом:

для исследуемой Ring-LAN, обслуживающей пользователей в диалоговом режиме, известны:

- типы  устройств, где =;

- количество  устройств разных типов;

- структура S связей между устройствами;

- производительность канала связи;

- объем  сообщения, передаваемого по каналу от узла ki ;

- интенсивности  обслуживания;

- контура q потоков заявок, где  ;

- количество   заявок в замкнутом контуре q;

- вероятности , перехода заявок контура q из обслуживающего узла ki в узел kj .

Необходимо рассчитать такие характеристики Ring-LAN, как интенсивности  потока сообщений, средние времена откликов  сообщений каждого замкнутого контура  и коэффициенты  загрузки для каждого узла ki.

В последующих параграфах для математической формулировки поставленной задачи и ее решения используется метод контуров, все шаги которого иллюстрируются единым учебным примером расчета характеристик для простейшей Ring-LAN.

 

4.2. Математическая формулировка

Математическая формулировка задачи предусматривает выявление всех узлов сети, обслуживающих сообщения, введение всех символьных обозначений для обслуживающих узлов, их характеристик и параметров Ring-LAN, и последующую запись всех необходимых линейных и нелинейных уравнений. Для выполнения этих преобразований применяют первые пять этапов метода контуров.


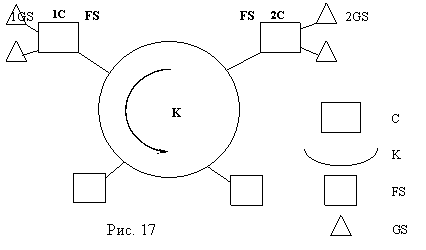
Описание структуры Ring-LAN иллюстрируется примером 4.1, представленным на рис. 17.

Пример 4.1. Структура Ring-LAN содержит: файл-серверы (1FS, 2FS), которые в режиме локального доступа через кольцевой канал (K) связи, коммуникационные контроллеры (1C, 2C) обслуживают в диалоговом режиме рабочие станции (1S — 20S), которые объединены в две группы (1GS , 2GS).

 


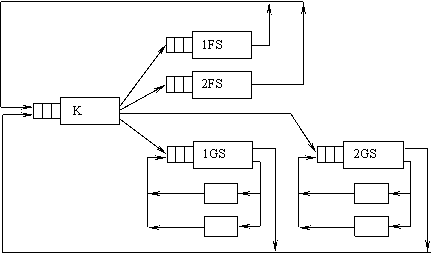
При составлении функциональной структуры проектировщик выделяет те обслуживающие устройства, которые имеют существенное влияние на временные оценки функционирования Ring-LAN. Определяются типы m обслуживающих узлов. В функциональной структуре, которая представлена на рис. 18, выделены три типа обслуживающих узлов FS, K, S и задается количество узлов Nm каждого типа. Принимаем, что задержки на обслуживание в контроллерах (C) учитываются параметрами канала K, поэтому на функциональной структуре, изображенной на рис.18, контроллеры (C) не представлены.


                                                               Рис.18.

 

Пример 4.2. В представленной Ring-LAN принимаем интенсивности  обслуживания, где m = 1 для FS, m = 2 для K, m = 3 для S.

 В рассматриваемом примере количество Nm обслуживающих узлов различных типов m соответственно равно: N1 = 2, N2 = 1, N3 = 20.

Кольцевой канал К связи участвует в передаче сообщений всех контуров q, причем в соответствии с циклической процедурой передачи принимаем, что квант времени  последовательно выделяется отправителям сообщений, которыми являются FS и S. Время задержки сообщений в канале связи равномерно распределено в интервале [, (N1+N3+1)]. Наименьшему значению соответствует случай, при котором сообщение поступило для передачи по каналу связи в тот момент, когда соответствующему отправителю предоставлен квант времени. Наибольшему значению интервала соответствует такой случай, при котором сообщение ожидает полный цикл выделения квантов времени. Тогда математическое ожидание времени  задержки в канале связи и дисперсия  времени задержки сообщений вычисляются, соответственно, по следующим соотношениям:

= 0,5(N1 + N3 + 2) ,   где   = / ;                           (20)

(N1 + N3)2 2 /12.                                                (21)

 

При составлении графовой модели сначала вводится единая нумерация всех обслуживающих узлов. Каждый узел обозначается стрелкой ki, где i =  и  N = . Затем описывают состав узлов в каждом контуре q и значения вероятностей перехода сообщений каждого контура q от узла ki к узлу kj . Всвязи с тем, что сообщения при обслуживании должны проходить канал связи дважды, при описании каждого контура необходимо использовать две фазы обслуживания  и . Введенная нумерация позволяет ввести символьные обозначения и записать все исходные данные для расчета характеристик. Графовая модель примера 4.2 приведена на рис. 19

 

 


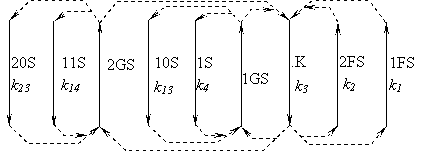
                                                               Рис. 19

 

Пример 4.3. Графовая модель рассматриваемой Ring-LAN содержит узлы k1, k2, которые моделируют файл-серверы (FS), узел k3 моделирует канал (K), узлы k4 -- k23 моделируют рабочие станции S.

В представленном варианте Ring-LAN узлы обслуживают 20 замкнутых контуров (). В рассматриваемом примере принимаем, что одна часть контуров обслуживается файл-сервером, моделируемым узлом k1, другая часть — файл-сервером k2. Тогда имеем два типа контуров q .   В контурах первого типа ( q = ) участвуют узлы k1, k3, ki, k3, где i = .   В контурах второго типа (q = ) участвуют узлы k2, k3, ki, k3, где i = . Все рассматриваемые контура q имеют простую конфигурацию, которой соответствуют вероятности перехода pi,j,q, = 1,0 .

Узлы k1, k2, моделируются обслуживающими системами M/M/1, которые обслуживают сообщения с интенсивностями  = 10 1/s и

 = 6 1/s и в соответствии с соотношением (12) имеют == 0,9 .

Узел k3 моделируется обслуживающей системой M/G/1 и осуществляет передачу сообщений  длиной z = 4000 byte , со скоростью w = 4,0  Mbit/s. В соответствии с соотношениями (21), (22) узел k3 имеет квант времени передачи= 0,008 s, математическое ожидание времени задержки в канале связи = 0,1 s и дисперсию времени задержки сообщений = 0,002821. Также в соответствии с соотношением (12) узел k3 имеет = 0,95.

Узлы k4, — k23,  моделируются обслуживающими системами M/M/1 без очередей и обслуживают сообщения с интенсивностями 

 = 0,333 1/s.

 

Составление линейных уравнений баланса выполняется для интенсивности  потока сообщений контура q для каждого узла ki с использованием соотношения (9). Для замкнутых контуров Ring-LAN в качестве базисной интенсивности  принимается интенсивность  в рабочей станции для соответствующего контура:

=,          где  .                                                        (22)

Тогда интенсивность  потока сообщений в канале связи зависит от количества контуров q и от количества фаз :

 =                                                                           (23)

 

Пример 4.4. Для рассматриваемой Ring-LAN на основании линейных уравнений и учитывая, что вероятности перехода  и что k4 — k8, k14 — k18 обслуживает k1, можно получить следующие соотношения для контура  для фаз  и :

 =  =  =  =  ,  a1,q=1,   для ,

                a2,q= 1  для ,  и тогда 

,           = 10 + 10   .   (24)

 

Для каждого контура q составляется нелинейное уравнение баланса, и при этом используются соотношения (6) и (10). Так как каждая станция работает в диалоговом режиме, количество сообщений  в каждом контуре равно 1.

 

Пример 4.5. Для контура  рассматриваемой Ring-LAN нелинейное уравнение баланса имеет следующий вид:

= 1 = 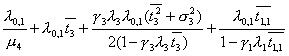  .           (25)

Каждое слагаемое соответствует одному из узлов, входящих в рассматриваемый контур. Первое слагаемое учитывает функционирование узла k4 , который соответствует станции S1 первой группы 1GS. Второе и третье слагаемые учитывают функционирование узла k3 , который соответствуют каналу связи. Последнее слагаемое учитывает функционирование узла k1 , который соответствует файл-серверу FS1. Коэффициент ограниченности очереди вычисляется по соотношению (11).

Таким образом, соотношения вида (24) и (25) составляют основу математической модели функционирования Ring-LAN.

 

4.3. Алгоритм решения

Записанная математическая модель функционирования Ring-LAN обеспечивает переход к вычислению функциональных характеристик. Алгоритм вычисления состоит из следующих шагов.

1. Задаются численные значения для исходных данных, к которым относятся: N, Q, pi,j (i,j = ), ,  .

2. Для каждого контура q на базе решения системы линейных уравнений вида (23) рассчитывают коэффициенты ai,j и выводятся соотношения вида (24).

3. Для каждого узла ki по соотношению (12) вычисляются значения . Если станция обслуживает в диалоговом режиме одно сообщение, то  =0.

4. Система нелинейных уравнений содержит Q уравнений вида (25). Решение системы нелинейных уравнений можно производить итеративно, как описано в параграфе 2.4.  Для шага s=0  диапазон рассчитываемой интенсивности базисного потока сообщений для уравнений контура q  находится в интервале между 0 и , где - интенсивность обслуживания сообщений станцией S.  Результатом итеративного расчета являются  .

5. По вычисленным ai,j и . для  каждого контура q и каждого узла ki по соотношениям (8) и (3) определяем  и . Затем вычисляем для каждого контура q время ответа  в диалоговом режиме и коэффициенты  загрузки узлов.

 

Пример 4.6. Для рассматриваемой Ring-LAN приведем результаты расчета характеристик :

1. Все численные значения исходных данных, которые необходимы для выполнения расчетов, приведены в примере 4.2 при описании графовой модели.

2. Значения вычисленных ai,j приведены в табл. 2.

3. Значения вычисленных  приведены в табл. 2.

4. Значения вычисленных  равны 0,09821/s; 

 0,04921/s.

 

Таблица 2. Рассчитанные параметры и характеристики Ring-LAN


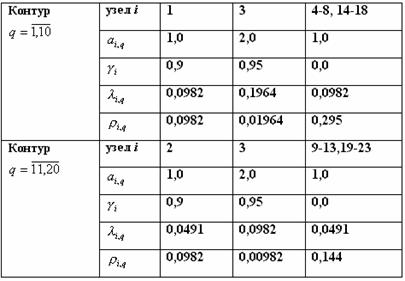
5. Значения вычисленных  и  проведено в табл. 2,

6. Значения вычисленных характеристик функционирования Ring-LAN равны:

- средние времена откликов  сообщений каждого замкнутого контура :   7,183 s,  17,366 s,

 - коэффициенты  загрузки для каждого узла .:

 файл-серверов FS:                0,982,  0,982,

 канала К:                0,2946,

 рабочих станций S:    

               = 0,295,

            =0,144;

 

 

 

4.4.Упражнения

Контрольные вопросы

1. Каким образом учитывается в Ring-LAN влияние коммуникационного контроллера GS на время обмена сообщениями?

2. Почему для моделирования канала связи Ring-LAN используется обслуживающая система M/G/1?

3. Почему для узлов k4 — k23 соответствующие коэффициенты

  = 0?

4. Каким образом осуществляется описание контуров Ring-LAN?

5. Какой физический смысл имеет каждое слагаемое в соотношении (25)?

6. Сколько независимых уравнений имеет система нелинейных уравнений в рассматриваемой Ring-LAN?

 

 

Задания

1. Составьте и решите нелинейные уравнения, аналогичные (25), если для узлов k4 — k14  = 0,33 1/s  и k15 — k24  = 0,2 1/s.

2. Составьте нелинейные уравнения для q = 2 и q = 6, докажите, что они нелинейные уравнения для q = 1 и q = 2 аналогичны.

3. На основании анализа результатов расчета (см. Табл. 2) и примера 3.6 найдите перегруженный участок рассматриваемой Ring-LAN.

4. Составьте нелинейные уравнения, учитывающие время задержки в GS, рассматриваемой Ring-LAN.

5. Какое предельное количество пользователей Ring-LAN в каждой группе могут обслужить ресурсы сети при времени ответа, не превышающем 3 с ?

 

 

 Список литературы

 

                1. Абросимов Л.И. Расчет характеристик вычислительных систем сложной конфигурации с помощью контуров.// Изв. АН СССР. Сер. Техн. кибернетика.1983. N 5. С .98—106.

2. Методы автоматизированного проектирования систем телеобработки данных: Учеб. пособие для вузов/ В.А. Мясников,

Ю.Н. Мельников, Л.И. Абросимов. М.: Энергоатомиздат, 1992. 288 с.

3. Клейнрок Л. Вычислительные системы с очередями. М.: Мир, 1979. 600 с.

4. Шварц М. Сети связи: протоколы, моделирование и анализ: В 2-х ч. .М: Наука, 1992. 272 с.

5. Захаров Г.П. Методы исследования сетей передачи данных.-М.: Радио и связь, 1982. 208 с.

6. Garcia-Lunes-Aceves,J.J. Loop-Free Routing Using Diffusing Computations IEEE/ACM transactions on Networking,1(1993)1,S.130—141.

7. Hariri S., Choudhary A., Sarikaya B. Architectural Support for Designing Fault-Tolerant Open Distributed Systems  Computer, 25(1992)6.S.50—62.

8.   http://www.rz.tu-ilmenau.de/~ubweb/web/ub.htm

9. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1973. 831 с.

 

 

 

 

 

 

 

 

 

 

Учебное издание

 

 

Абросимов Леонид Иванович

 

АНАЛИЗ И ПРОЕКТИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ

 

Учебное пособие

по курсу "Сети ЭВМ"

для студентов, обучающихся по направлению "Информатика и вычислительная техника" и по специальности "Вычислительные машины, комплексы, системы и сети".

 

               

Редактор издательства О. М. Горина

ЛР № 020528         от 05.06.97            

____________________________________________________________________

Темплан издания МЭИ 1999 г. (II), учебн.

Подписано к печати   10.01.2000                                        Печать офсетная

Формат 60х84/16                  Физ. печ. л. 3,5                                                    

Тираж 300             Изд № 182             Заказ                      Цена 3 руб. 70 к.

____________________________________________________________________

Издательство МЭИ, Россия, 111250, Москва, Красноказарменная, д. 14

Типография ЦНИИ "Электроника", Россия, 117415, Москва,

просп. Вернадского, д. 39