BC/NW 2007, №1, (10) :4.2

ГЕНЕРАТОРЫ СРЕДНИХ ПО СЛОЖНОСТИ СТРУКТУР ДЛЯ ИССЛЕДОВАНИЯ БАЗОВЫХ АЛГОРИТМОВ СТРУКТУРНОЙ ИНФОРМАТИКИ

И.Н. Карпухин, С.В. Яркин, В.А. Кохов

(Москва, Московский энергетический институт (технический университет), Россия)

Получение оценки вычислительной сложности решения NP-полных задач в среднем остаётся открытой проблемой в теории вычислительной сложности задач. В докладе приведена программная реализация оригинального метода, предложенного Коховым В.А, для построения генераторов графов из разных семейств с тремя уровнями сложности: (1) низким; (2) средним; (3) высоким. В качестве универсальной меры сложности графов принят индекс структурной сложности в базисе B [1]. Программные комплексы разработаны в виде генераторов графов, которые расширяют функциональное наполнение ППП «Полигон-Стрин» и используются в учебном процессе студентов для выполнении лабораторных работ и курсовых проектов при определении экспериментальных оценок вычислительной сложности алгоритмов решения труднорешаемых задач, таких как, распознавание изоморфизма графов, определение изоморфного вложения одного графа в другой, определение максимального общего фрагмента графов, определение всех автоморфизмов графа.

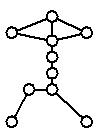
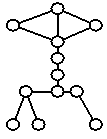
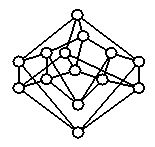
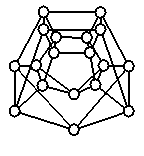
На рис.1 приведены примеры диаграмм графов средних по сложности в базисе цепей для двух классов графов: (1) графы с двумя базовыми циклами; (2) регулярные графы степени 4.

Средние по сложности графы с двумя базовыми циклами

Средние по сложности регулярные графы степени 4

Рис. 1. Представители двух бесконечных классов графов средних по сложности

ППП «Полигон-Стрин» входит в учебно-методический комплекс «Основы структурной информатики» и используется для обучения студентов первого и второго курсов всех направлений обучения в МЭИ [2]

Литература

1. Кохов В.А. Концептуальные и математические модели сложности графов. — М: Изд-во МЭИ, 2002.-160 с.

2. Кохов В.А., Ткаченко С.В., Незнанов А.А. Решение базовых задач структурной информатики с помощью ППП «Полигон-СТРИН». – М.: Издательство МЭИ, 2005. – 116 с.