BC/NW 2007, №2, (11) :11.5
МЕТАПЛАНИРОВЩИК - ГЕНЕРАТОР СТРАТЕГИЙ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ [1]
В.В. Топорков, А.С. Целищев, А.В. Бобченков, П.В. Рычкова
(Москва, Московский Энергетический Институт (ТУ), Россия)
При организации вычислений в распределённых средах возникает задача планирования и распределения ресурсов, которая не имеет универсального подхода к её решению. В [1] описана процедура планирования на основе масштабируемой модели вычислений1, ставящая своей целью оптимизацию выполнения программ путём выбора конфигурации вычислительных ресурсов, приведён оригинальный метод критических работ. В докладе рассматриваются некоторые аспекты программной реализации метода критических работ. Рассмотрены решения проблем, возникающих при работе со случайно сгенерированными графовыми моделями, а также предложены оригинальные вспомогательные алгоритмы.
Масштабирование состоит в итеративном применении двухэтапной процедуры:
1. Планирование и назначение последовательно выделяемых критических работ – путей наибольшей длительности.
2. Разрешение возникающих коллизий путём изменения назначения соответствующей операции.
Первый этап предполагает поиск и ранжирование критических работ программной модели, который сводится к поиску критических путей во взвешенном ориентированном графе, отражающем модель. В [2] предложен способ поиска критических работ на основе поиска в глубину, который, однако, требует большого количества вычислений на графах большой размерности и требует введения ограничений для предотвращения зацикливаний. Для программной реализации составления списка критических путей в графе предложен гибридный алгоритм, объединяющий в себе элементы алгоритма Форда [3] и алгоритма Йена [4], состоящий из двух этапов:
1. Рекуррентное построение корневого дерева критических работ графа с вершинами-работами.
2. Формирование массива критических работ путём перебора вершин дерева.
Первый этап начинается с построения корня дерева. Корнем дерева D0 является самый длинный критический путь в исходном взвешенном ориентированном графе-модели G={U,V}, который находится с помощью любого из известных алгоритмов поиска максимального пути в графе (в программной реализации использован алгоритм Форда). Вершины первого яруса корневого дерева соответствуют критическим путям в графах Gi={Ui=U \ ei,V}, i=1..N, где N – число рёбер в самом длинном критическом пути, соответствующем корню дерева, получаемых удалением i-го ребра ei из графа G (критические пути находятся как и для корня алгоритмом Форда). Вершины второго яруса, инцидентные i-ой вершине первого яруса соответствуют критическим работам в графах Gij={ Uij=Ui \ eij, V}, j=1..M, где M – число рёбер в критическом пути, соответствующем графу Gi. Вершины k-го яруса, инцидентные l-ой вершине k-1-го яруса соответствуют критическим работам в графах Gij..s={ Uij..s=Uij..s-1 \ eij..s, V}, s=1..P, где P – число рёбер в критическом пути, соответствующем графу k-1-го яруса. Вершина дерева становится листом (то есть для неё не вычисляются критические пути на следующих ярусах) в двух случаях: когда критический путь, соответствующий вершине имеет лишь одно ребро, либо соответствует полученной ранее вершине корневого дерева. Так как часть ветвей дерева, соответствующих его листам, не вычисляется, сокращается и число вариантов перебора. Построение дерева прекращается при невозможности дальнейшего построения. Один из вариантов реализации предложенного алгоритма построения корневого дерева предполагает следующие шаги:
1. Поиск критического пути и вершины D0. Текущий ярус n=0.
2. Если все вершины текущего яруса листы – прекратить построение.
3. n:=n+1, определить число вершин текущего яруса
4. Поиск критический путей, соответствующих вершинам текущего яруса (каждый путь, соответствующий вершине, ищется для графа, в котором удаляется одно ребро критического пути, соответствующего вершине n-1 яруса, инцидентной рассматриваемой вершине текущего яруса)
5. Определение вершин-листов (см. условия выше)
6. Переход к шагу 2.
Общий вид дерева критических путей графа представлен на рис. 1. Стоит отметить, что при программной реализации построения дерева на языке Java для проверки дублирования путей и определения листов дерева используется механизм коллекций с применением динамического программирования.
Второй этап предполагает получение упорядоченного списка критических путей исходного графа G={U,V} из дерева критических путей, полученного на первом этапе. Предложен следующий алгоритм:
1. U’ = {} – множество рёбер, M – список-массив критических работ, i=0
2. Если U’ = U , конец работы алгоритма
3. Поиск пути и соответствующей ему вершины Di с наибольшим весом в дереве критических путей
4. U’=U’ V U’’ , где U’’ – ребра пути, соответствующего вершине Di.
5. M[i] := Di (подразумевается, что в элементе массива сохраняется критический путь, то есть вершины и рёбра, входящие в него)
6. i:=i+1
7. Удаление вершины Di из построенного дерева (в данном случае под удалением понимается тот факт, что эта вершина не рассматривается в качестве кандидатов на шаге 3).
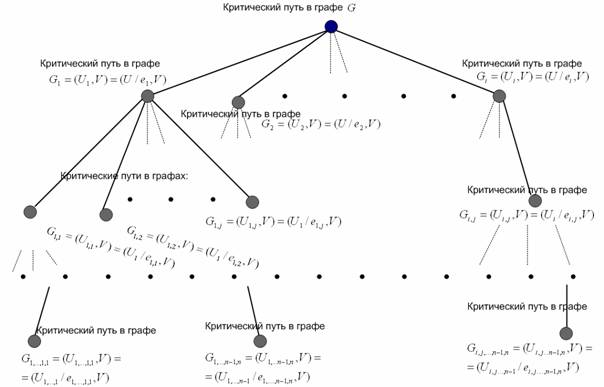
Рис. 1
После получения массива критических путей можно приступать к планированию и назначению вычислительных ресурсов. Планировщик должен принимать на вход ориентированный граф, предварительно разбитый на критические работы, а на выходе формировать вектор априорных оценок времени для каждой из задач-вершин графа на основе однокритериальной (в общем случае многокритериальной, однако при программной реализации была использована однокритериальная) оптимизации.
Требования к входным данным заключаются в следующем: критические работы должны быть ранжированы, то есть, упорядочены по априорному времени исполнения. За оценку времени исполнения работы принимается сумма времен исполнения каждой из задач работы на самых быстрых процессорах плюс сумма времен обменов данными между задачами.
Критические работы задаются задачами, входящими в них, и информационными связями, выражающими отношение предшествования. Кроме этого, к входным данным относятся значения производительности процессоров для каждой из задач.
Алгоритм работы планировщика включает в себя цикл, проходящий по всем критическим работам. В результате одной итерации получается один или несколько вариантов распределения, которые являются подвекторами искомого вектора, являющимся результатом решения всей задачи планирования.
На каждой итерации в подвектор включаются значения априорных оценок времени для соответствующих задач из текущей критической работы. Если в начале итерации имеется несколько вариантов, то рассматривается каждый из них. В течение этого процесса в список могут добавляться новые варианты распределения, однако они будут рассматриваться уже на следующей итерации для следующей критической работы.
Тело цикла:
1) Если
количество нераспределенных задач текущей критической работы больше единицы, то
строится дерево поиска, согласно методу, описанному в [2], и производится
оптимизация. После построения дерева, обратной и прямой прогонки на выходе
имеется один или более ответов – подвекторов, содержащих априорные оценки для
задач данной критической работы, так как в результате прямой прогонки может
быть найдено несколько экстремумов критериальной функции. Если дерево построено
для первой критической работы, множество ответов переносится в список вариантов
распределения. В противном случае производится слияние найденных ответов и
существующих вариантов распределения. Если дерево строится не для первой
критической работы, и к моменту данного шага уже существует m вариантов
распределения, в результате нахождения n ответов на данном шаге будет
получаться m*n выходных вариантов к началу следующей итерации.
Все задачи, входящие в данную критическую работу, на последующих итерациях
считаются распределенными. Существует возможность того, что дерево поиска не
даст ответа, что может произойти в результате слишком сильного ограничения по
времени (или другой свободной переменной), в таком случае текущий
рассматриваемый вариант считается недействительным и вычеркивается из списка.
2) Если работа содержит одну нераспределенную задачу, то определяются новые временные границы, заданные уже распределенными задачами. Если существует процессор, на котором задача может быть выполнена за это время, тогда значение априорной оценки времени выполнения для данной задачи на данном процессоре запоминается. Если это невозможно, текущий рассматриваемый вариант вычеркивается из списка и на последующих итерациях не рассматривается. Количество вариантов на данной итерации остается прежним либо уменьшается.
3) Если работа содержит только обмен данными, что может произойти в случае, если работа состоит из двух задач, и обе к моменту рассмотрения работы являются распределенными, то также вычисляются новые временные границы. Может возникнуть нижеописанная ситуация несовместимости распределений отдельных критических работ, в таком случае текущий рассматриваемый вариант также отбрасывается.
4) Если работа содержит изолированную задачу, соответствующую изолированной вершине, за ее априорную оценку принимается все время оптимизации, заданное для набора критических работ (задания). Это обусловлено конкретным критерием планирования, использующимся в программной реализации – средней загрузке базовых процессоров. При других критериях априорная оценка времени для изолированной задачи может быть другой. Количество имеющихся вариантов распределения на этой итерации сохраняется.
5) Когда распределены задачи всех критических работ, либо не осталось вариантов распределения в результате их вычеркивания, алгоритм завершает свою работу.
В результате работы алгоритма формируется множество векторов априорных оценок времени (вариантов распределения) для всех задач. Эти данные используются в дальнейшем для назначения вычислительного ресурса (процессоров). Стоит отметить, что в результате тестирования реализованного модуля планировщика были выявлены следующие исключительные ситуации:
1) В том случае, когда две работы не имеют общих вершин, и распределяются независимо друг от друга, и между некоторыми двумя вершинами существует дуга (информационная связь), такая дуга может войти в состав отдельной работы, к моменту обработки планировщиком которой обе вершины на концах дуги будут распределены. При этом полученное распределение не позволит соблюсти отношение предшествования, то есть задача, связанная с вершиной начала дуги будет выполняться позже или одновременно с задачей конца дуги. Таким образом, при оценке запаса времени на обмен получаем недостаточное или даже отрицательное значение.
2) Отличается от предыдущего случая тем, что некоторая работа включает одну или более нераспределенных задач между уже распределенными. Так же, запаса времени, жестко заданного уже распределенными концевыми задачами работы может быть недостаточно для их исполнения даже на самом производительном процессоре.
Данные ситуации можно избежать, проведя преобразования над исходной моделью-графом, что, однако, не входило в рамки программной реализации метода критических работ.
Второй этап процедуры масштабирования состоит в разрешении коллизий, возникающих при последовательном назначении вычислительных ресурсов для задач каждой критической работы. Представление коллизий двудольным графом (X, Y, A), множество рёбер А которого отражает попарную конкуренцию за ресурс, а также методы их оптимального и условно оптимального разрешения предложены в [1]. В процессе реализации методов были предложены эвристики, позволяющие в некоторых случаях получать более близкие к оптимальному варианты решений. Далее приведёны основные шаги реализованного алгоритма (подразумевается, что коллизия уже представлена двудольным графом так, как это описано в [1], Х – множество вершин, соответствующих задачам, вызвавшим коллизии, Y – множество вершин, соответствующих распределённым задачам):
1. Для каждой вершины из X, необходимо найти вершину-представитель из Y, с которой она вступает в коллизию. При этом вершина-представитель должна выбираться из вершин, инцидентных вершине, соответствующей задаче, вызвавшей коллизию, и иметь минимальный вес. Последовательность действий на данном этапе такова:
a. Из множества Y последовательно выбираются вершины со степенью, равной единице (то есть с одним инцидентным ребром). Выбор происходит в порядке увеличения веса. Каждая такая вершина будет вершиной-представителем для инцидентной ей вершины из Х.
b. После шага а возможна ситуация, когда остались вершины из Х, для которых не найдены вершины-представители из Y. В таком случае применяется предложенный эвристический алгоритм:
i. Вершины из множества Х, для которых не найден представитель, упорядочиваются по возрастанию в соответствии с тем, сколько вершин из Y, не являющихся чьим-либо представителем, инцидентны данной вершине из Х.
ii. Для каждой вершины из полученного списка выбирается инцидентная вершина-представитель из Y с наименьшим весом.
Такой метод позволяет уменьшить вероятность ситуации, при которой существуют вершины в Х, для которых не может быть подобран представитель по причине того, что все инцидентные ей вершины из Y являются представителями других вершин из Х. Пример подобной ситуации приведён на рис. 2. Приведённая эвристика исключает выбор вершины p24 представителем для вершины p4 и последующей изоляции вершины p30, приводящей к исключительной ситуации.
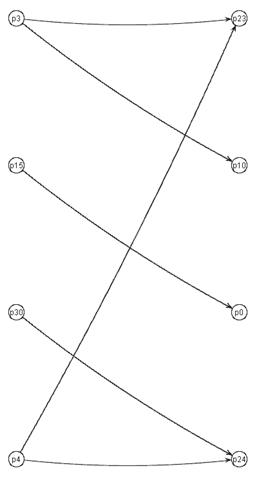
Рис. 2
2. Из каждой пары вершин, включающей в себя вершину из Х и её представителя в Y, выбирается одна вершина с наибольшим весом (в качестве веса вершин в двудольном графе могут выступать определённое на этапе планирования время выполнения задачи, соответствующей вершине). Задаче, соответствующей этой вершине назначается процессор, за который шла конкуренция. При этом если процессор переназначается с вершины из множества Y на вершину из множества Х, то для вершины из множества Y производится проверка на наличие других процессоров, на которых соответствующая ей задача может выполняться. В случае отсутствия таких процессоров переназначение процессора на вершину из множества Х не происходит.
3. Для каждой из вершин, которые не были выбраны на шаге 2, необходимо провести назначение процессоров, не задействованных в вычислениях. Данная процедура аналогична шагу 1 с тем лишь отличием, что двудольный граф (X,Y,A) таков, что Х – множество вершин, которые не были выбраны на шаге 2, Y – множество незадействованных процессоров, А – множество рёбер. Если существует ребро ai, соединяющее вершины xj и yk - это означает, что задача, соответствующая вершине xj может быть выполнена на процессоре yk. Процедура на данном шаге может учитывать в качестве критерия выбора процессора не только априорное время выполнения задачи на выбранном процессоре, а, например, значение стоимостной функции при назначении задачи на процессор.
Описанные выше алгоритмы положены в основу программной реализации процедуры масштабирования. Разработанное приложение, использующее технологии Java и Microsoft .NET позволяет генерировать случайные модели – информационные графы программ, проводить ранжирование критических работ для таких моделей, осуществлять планирование, назначение задач и разрешение коллизий.
ЛИТЕРАТУРА
1. Топорков В.В. Модели распределённых вычислений. М.: ФИЗМАТЛИТ. 2004. 320с.
2. Топорков В.В. Декомпозиционные схемы синтеза стратегий планирования в масштабируемых системах // Известия РАН. Теория и систеы управления. 2006. № 1. С. 82-93.
3. Lestor R. Ford jr., D. R. Fulkerson: Flows in Networks, Princeton University Press, 1962.
4. http://homepages.compuserve.de/chasluebeck/alg_1_8.htm