BC/NW 2007, №2, (11) :12.1
Моделирование нагрузки в системах передачи
потоковой информации
Куприянов А.Г.
(Москва, Московский энергетический институт (ТУ), Россия)
Потоковое Видо-По-Запросу через Интернет является важным шагом в эволюции средств доставки потокового видео. На данный момент все существующие системы Виде-По-Запросу являются прототипами. Ключевой проблемой является вопрос, как разработать архитектуру системы, которая будет легко масштабирована под требования многих заказчиков, будет обладать низкой стоимостью обслуживания, отличаться малой латентностью, предоставлять высокое качество видео и обладать разумной стоимостью внедрения. В решении данной проблемы разработчику могут оказать большую помощь имитационные модели разрабатываемых архитектур для проверки на покрытие всех вышеописанных требований. Одним из первых шагов при построении моделей системы Видео-По-Запросу является моделирование нагрузки на систему, другими словами моделирование пользовательских запросов. В данной статье будут представлены три основные модели, описывающие поведение пользователей в системах Видео-По-Запросу.
Основным
фактором, определяющим распределение пользователей, является популярность видео
файла. К второстепенным факторам, влияющим на частоту запросов пользователей к
тому или иному файлу, может быть отнесены механизмы рекомендаций, встроенные в
интерфейс пользователя, длина файла, а также время суток, но эти факторы в
данной статье не рассматриваются. Однако разрабатываемая модель может быть
легко адаптирована под дополнительные требования. В качестве среды разработки
модели будем использовать среду моделирования Matlab:Simulink.
Основными входным данными для нашей модели является количество доступных файлов Nv. Для Matlab данный параметр будет иметь обозначение INPUT_Number_Of_Files. Пусть популярность i-го видео будет pi (фактически вероятность обращения к i-му файлу), где i принадлежит [1, Nv]. Считаем, что все файлы упорядочены в порядке убывания популярности. Таким образом, файл с наименьшим индексом имеет наибольшую популярность. Следующим параметром, определяющим поведение модели, является интенсивность пользовательских запросов INPUT_Requests_Intensivity.
Для серверов потокового видео в Интернете зависимость обращения к какому-либо файлу напрямую зависит от его рейтинга. Такая зависимость не является линейной и подчиняется закону Ципфа (Zipf).
Закон Ципфа пришел из лингвистики и гласит, что если все слова некоторого языка (или просто достаточно длинного текста) упорядочить по убыванию частоты их использования, то частота n-го слова в таком списке окажется приблизительно обратно пропорциональной его порядковому номеру n (так называемому рангу этого слова).
В законе Ципфа популярность i-го видео пропорциональна 1/iς, где ς является параметром Ципфа. Во многих источниках ς принимается равным 1, однако наиболее правдоподобным является значение 0,27.
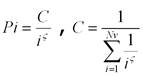
Для построения модели понадобится дополнительный параметр, такой как временной отрезок INPUT_Simulation_Time. Сама модель Simulink представляет собой сгенерированный по заданному закону массив пользовательских запросов OUTPUT_Request_Sequence_Х (значение элемента массива – номер файла) в качестве источника данных и блок-селектор осуществляющий вывод элементов массива с заданной интенсивностью.
Алгоритм построения массива достаточно тривиален. Его условно можно разбить на три этапа.
1. Определение вероятности запроса для каждого из файлов.
2. Определение числа запросов к каждому из файлов в зависимости от интенсивности запросов и времени симуляции.
3. Назначение элементов массиву запросов.
Найдем общее число запросов за заданный
промежуток времени:
OUTPUT_Number_of_Requests =
INPUT_Simulation_Time
/ INPUT_Requests_Intensivity
Затем, в
соответствии с формулой закона Ципфа определим вероятность Pi для каждого файла. Введем величину Ri,
определяющую число запросов к каждому из файлов.
Ri = Pi x OUTPUT_Number_of_Requests.
Создадим временный
массив TmpArray [2], в который
последовательно запишем все запросы ко всем файлам. Для того, чтобы запросы
имели произвольную последовательность следует применить встроенную функцию Matlab – randperm. В итоге выходной массив запросов будет
OUTPUT_Request_Sequence_Zipf = randperm (TmpArray);
Из-за
тривиальности алгоритма код программы в данной статье приводить не будем,
однако как видно из описания, данный алгоритм
легко можно реализовать на любом ЯВУ, в том числе встроенном языке Matlab.
Следующим распределением, описывающим зависимость пользовательских запросов от популярности, является геометрический закон распределения. В геометрическом законе разница между популярностями pi и pi-1 является постоянной величиной. Пусть знаменатель прогрессии равен δ (0 ≤ δ ≤1). Так как pi / (pi-1) = δ , то можно выразить pi, где 1≤ i ≤Nv

Последовательность действий в алгоритме генерации массива запросов весьма схожа с предыдущим законом. Введена еще одна переменная INPUT_Q_Parameter, соответствующая δ. Реализация данного распределения отличается от предыдущего лишь первоначальной частью определения вероятностей. В остальном алгоритм идентичен.
Последним законом, описываемым в статье, является правило 80-20. Эта несколько упрощенная модель реализует следующую зависимость: 80% поступающих запросов приходится на 20% наиболее популярных объектов. (Иногда для большей точности указывается 23%). А на 10% самых популярных объектов – 60% нагрузки. Как и для геометрического закона приведем лишь код для генерации pi. Для начала определим число файлов входящих в 10, 20 и 80%. Затем следует разделить запросы между всеми файлами, входящими в определенную группу. После получения Pi дальнейший алгоритм идентичен предыдущему.
В результате получили 3 массива, хранящие
запросы пользователей в соответствии с заданными распределениями. Для включения
данных массивов в модель Simulink
построим субфункцию генерации сигналов с заданной интенсивностью. Данная
субфункция приведена на рис. 1. В
красной области содержатся непосредственно три массива с распределениями.
Зеленая область содержит переключатель между распределениями. Константа Type_Of_Distribution задаёт конкретное распределение. Синяя область содержит логику, в
которой сумматор Next_Index осуществляет переход новому
элементу массива с частотой INPUT_Requests_Intensivity,
которая была описана в начале статьи.
В
процессе моделирования пользовательской нагрузки можно снять гистограммы
выходного сигнала Request. В
результате получим диаграммы, приведенные на рис. 2.
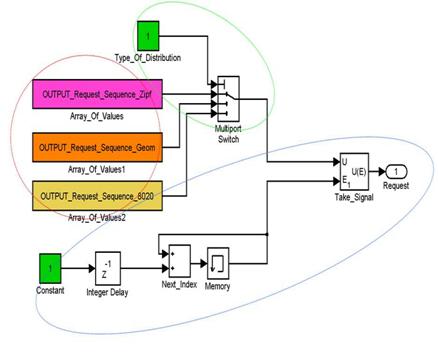
Рис. 1. Модель пользовательских запросов в Matlab:Simulink
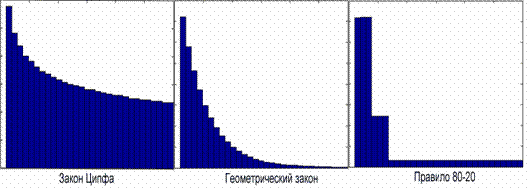
Рис. 2. Гистограммы распределений
В результате получили модель, генерирующую запросы пользователей с различными законами распределения, каждый из которых имеет свою область применения.
Распределение Ципфа является распределением с «толстым» хвостом, т.е. этим хвостом нельзя пренебрегать. Данный закон хорошо описывает системы с большим числом пользователей и небольшим количеством файлов, когда «каждый файл находит своего пользователя».
Геометрическая зависимость описывает поведение пользователей в системах, в которых число файлов высоко, так, что обращения к непопулярным файлам практически отсутствуют.
Распределение 80-20, несмотря на свою кажущуюся грубость, может применяться в системах с кэширующими механизмами, имея 10% файлов в КЭШе можно обслуживать более половины запросов. Каждая из моделей описывает различные типы систем Видео-По-Запросу, а благодаря изменяемым параметрам разработанные модели позволяют охватить системы практически любого масштаба.
ЛИТЕРАТУРА
1. Zheng W. Understanding User Behavior in Large-Scale
Video-on-Demand Systems. Computer Science Department, U. C.
2. Schoppek W.
Opportunities and Challenges of Modeling User Behavior in Complex Real World
Tasks.