BC/NW 2007, №2, (11) :12.2

ПРИМЕНЕНИЕ ПОДХОДОВ ИЗ ОБЛАСТИ СЖАТИЯ ДАННЫХ С ПОТЕРЯМИ ПРИ СЖАТИИ БЕЗ ПОТЕРЬ НА ПРИМЕРЕ ВЕЙВЛЕТНОЙ КОМПРЕССИИ ИЗОБРАЖЕНИЙ

П.А. Чернов

(Москва, Московский Энергетический Институт (ТУ), Россия)

Существующие методы сжатия изображений без потерь можно разделить по типу используемой базовой схемы сжатия. В основе лучших современных схем сжатия изображений без потерь лежит принцип предиктивного кодирования [1].

Характеристики соседних точек изображения сильно коррелированны. При этом корреляция экспоненциально убывает с увеличением расстояния между точками [2]. Чтобы учесть эту корреляцию стали применять предиктивные схемы.

Ключевой компонентой предиктивной схемы является блок предиктора. Задачей предиктора является максимально точное прогнозирование характеристик очередной кодируемой точки изображения. На основе спрогнозированных и реальных характеристик точки вычисляется ошибка прогноза, которая подлежит сжатию. Как правило, полученная ошибка имеет распределение, близкое к двойному экспоненциальному (ДЭР) [3, 4]. Функция плотности ДЭР (рис. 1, иногда ДЭР называют распределением Лапласа) аналитически задается следующим образом:

,

где b – параметр масштаба, a – математическое ожидание, е – число Эйлера.

Наиболее вероятной является малая величина ошибки предиктора, а вероятность ошибки с ее ростом по модулю экспоненциально убывает.

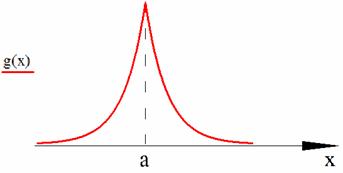
Рис. 1. График плотности ДЭР

Данные, имеющие ДЭР, хорошо сжимаются энтропийным кодером (ЭК, например, Хаффмана, Шеннона-Фано, Райса и Голомба, арифметическим и т.д.). Этот факт следует из сильной неравномерности ДЭР.

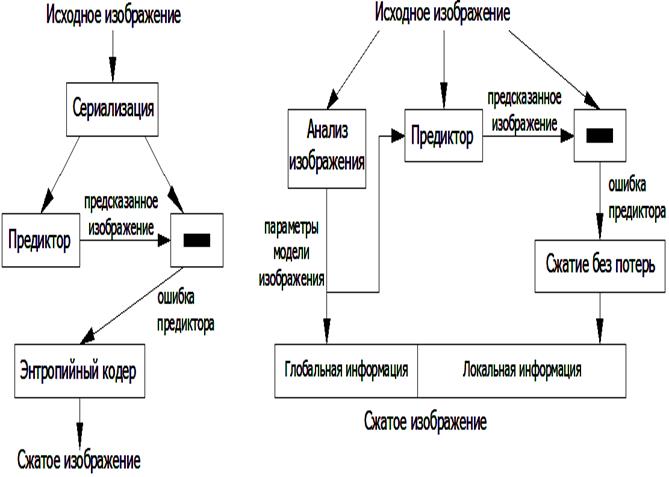
Первая подобного рода предиктивная схема (рис. 2, а) была предложена Говардом и Виттером [5]. Данная схема лежит в основе методов LOCO, JPEG-LS, SICLIC, ALPLIC [3, 6 – 8] и др.

а) б)

Рис. 2. Схемы сжатия изображений без потерь предложенные:

а – Говардом и Виттером, б – Мейером и Тишером

Следующим шагом в развитии предиктивных схем можно назвать появление схемы предложенной Мейером и Тишером [9]. Данная схема (рис. 2, б) предлагает выделить в сжатом изображении две части. Одна часть хранит так называемую «глобальную» информацию об изображении, представляющую собой служебную информацию предиктора, полученную в результате анализа исходного изображения. Эта служебная информация служит для получения более точного прогноза характеристик кодируемых точек на выходе предиктора. Вторая часть хранит «локальную» информацию – сжатую ошибку предиктора. В своей работе Мейер и Тишер показали превосходство предложенной ими схемы над схемой Говарда и Виттера по обеспечиваемому коэффициенту сжатия.

В схеме Мейера и Тишера блоки анализа изображения и предиктора по сути своей представляют аппарат построения аппроксимации изображения. Сама аппроксимация строится по довольно сложным правилам, которые и выделяют тот или иной метод, основанный на данной схеме, среди себе подобных [1].

Тезис 1: блоки анализа и предиктора можно заменить блоком сжатия изображения с потерями, в результате чего получить простое изображение-ошибку при малых затратах на хранение сжатого с потерями изображения.

Предположение: в полученном изображении-ошибке, как правило, сохраняется корреляция соседних точек, возможно, в меньшей степени, чем в исходном изображении.

Тезис 2: для изображения-ошибки может оказаться целесообразно применить сжатие рекурсивно – к изображению-ошибке применить схему сжатия, как к исходному изображению.

Тезис 3: предлагаемая схема сжатия изображений без потерь может быть с успехом обобщена до концептуальной схемы сжатия без потерь данных произвольной природы (рис. 3).

Тезис 4: по предлагаемой схеме можно осуществить прогрессивное сжатие (позволяющее получать более точные декодированные данные по мере поступления кодированных).

Рис. 3. Предлагаемая схема сжатия данных (изображений) без потерь

В качестве основы метода сжатия изображений с потерями предлагается использовать дискретное вейвлет-преобразование (ДВП). Выбор в пользу ДВП обусловлен тем, что алгоритмы сжатия с потерями построенные на основе ДВП позволяют получать хорошую аппроксимацию исходного изображения при высоких степенях сжатия. Доказательством тому можно считать существующие алгоритмы сжатия такие, как SPIHT, JPEG2000, EZW и др.

Можно предположить, что сжатие по предлагаемой схеме может быть выполнено относительно быстро. Существуют реализации фильтров 9/7, выполняющие вейвлет-преобразование картинки размером 512х512 точек за 0.4 секунды на P-166 [2]. Применение вычислительно несложных методов сжатия без потерь изображения-ошибки и вейвлет-коэффициентов (предварительно квантованных или разреженных), например, в виде простого ЭК, вероятно, не сильно увеличат время сжатия.

Автор статьи планирует доказать сформулированные выше тезисы 1-4.

ЛИТЕРАТУРА

1. Бредихин Д. Ю. Сжатие графики без потерь качества. – 2004. – 21 c.

http://www.compression.ru/download/articles/i_lless/
bredikhin_2004_lossless_image_compression.pdf

2. Воробьев В. П., Грибунин В.Г. Теория и практика вейвлет-преобразования. – С.-Петербург: Военный университет связи, 1999. – 203 с.

3. Weinberger M. J., Seroussi G. S., Sapiro G. LOCO-I: A Low Complexity, Context-Based, Lossless Image Compression Algorithm // HP Laboratories, Palo Alto – 1996.

4. Ekstrand N. Lossless Compression of Grayscale Images via Context Tree Weighting // In Proceedings Data Compression Conference (DCC), IEEE Computer Society Press – 1996. – P. 132-139.

5. Howard P. G., Vitter J. S. New Methods for Lossless Image Compression Using Arithmetic Coding // Information Processing and Management 28 – 1992. – P. 765-779.

6. Weinberger M. J., Seroussi G. S. From LOCO-I to the JPEG-LS Standard // Computer Systems Laboratory HP Laboratories, Palo Alto – 1999.

7. Barequet R., Feder M. SICLIC: A Simple Inter-Color Lossless Image Coder // Department of EE-Systems Tel-Aviv University – 1999. – P. 501-510.

8. Motta G., Storer J., Carpentieri B. Adaptive Linear Prediction Lossless Image Coding // Brandeis University, Computer Science Dept, Walltham MA-0254. Universita’di Salerno, Dip. Di Informatica ed Applicazioni “R.M. Capocelli”, I-84081 Baronissi (SA), Italy – 1999.

9. Meyer B., Tischer P. TMW – a New Method for Lossless Image Compression // Department of Computer Science, Monash University Clayton, Victoria, Australia – 1997.