BC/NW 2007, №2, (11) :13.4
Применение RS-стегоанализа для обнаружения LSB-стеганографии
Бобченков А. В., Бородин Г. А.
(Московский энергетический институт (Технический университет), Москва)
Стегоанализ – сравнительно новое направление исследований в сфере стеганографии. Стегоанализом, по аналогии с криптоанализом, называется задача, обратная по отношению к стеганографии, и заключается в обнаружении подозрительного контейнера, в который каким-либо методом могли быть включена посторонняя информация, с намерением скрыть сам факт ее нахождения. Данные, которые вносятся в контейнер, могут быть предварительно зашифрованы, чтобы усложнить задачу стегоаналитика, однако основная цель, стоящая перед ним – не извлечь информацию и прочитать, а по крайней мере обнаружить скрытый канал передачи данных [1].
Известно, что файлы графических форматов могут служить хорошим контейнером для стеганографической передачи данных, так как обладают необходимой информационной избыточностью. Одним из широко используемых методов стеганографии для изображений является LSB (least significant bits), который состоит в перезаписи младших бит изображения [1]. Визуально изображение при этом не изменяется, особенно если в качестве контейнера выбрано многоцветное изображение с большим количеством деталей, то есть информационно нагруженное. Это в значительной степени осложняет работу стегоаналитика, если он не обладает специальными средствами стегоанализа. В качестве таких средств могут выступать программы, реализующие статистические методы стегоанализа.
Одним из оригинальных методов статистического стегоанализа является метод RS, впервые опубликованным в 2001 г. коллективом ученых под руководством Дж. Фридрих [2,3]. Сокращение в названии расшифровывается как Regular-Singular, то есть «регулярно-сингулярный».
Суть метода состоит в следующем. Все изображение разбивается на группы по n пикселов G(x1,x2,…,xn), где n четно, например по 2 пиксела, находящихся рядом по горизонтали. Для группы пикселов определяется функция регулярности или «гладкости» f(G), в качестве такой функции можно выбрать, например, дисперсию значений внутри группы, либо просто сумму перепадов значений смежных пикселов. Под значением пиксела понимаем целое число от 0 до 255.
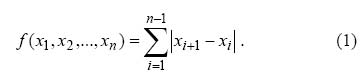
Функция F(x) называется флиппингом и имеет свойство F(F(x)) = x. Определим две функции флиппинга – F1, соответствует инверсии младшего бита пиксела, и F2, представляющая собой инверсию с переносом в старший бит (прибавление единицы).
F1: 0 ↔ 1, 2 ↔ 3, …, 254 ↔ 255
F-1: 255 ↔ 0, 1 ↔ 2, 3 ↔ 4, …,253 ↔ 254, 255 ↔ 0
При применении флиппинга к группе получаем преобразованную группу пикселов. Далее, поделим все группы пикселов на классы следующим образом:
- Регулярные группы: G ∈ R ⇔ f(F(G)) > f(G)
- Сингулярные группы: G ∈ S ⇔ f(F(G)) < f(G)
- Неиспользуемые группы: G ∈ U ⇔ f(F(G)) = f(G)
В дальнейшем нас будет интересовать соотношение между группами в изображении. Определим количество групп попавших в тот или иной класс как RM, SM, UM и R-M, S-M, U-M, где индексы M и –М означают соответственно применение F1 и F-1 для получения распределения. Наша цель – определить каким образом внедрение сообщения методом LSB будет влиять на вышеописанную статистику групп пикселов.
Метод основывается на статистическом предположении, что для естественного изображения, другими словами, незаполненного контейнера, характерно следующее:
RM ≅ R−M и SM ≅ S−M (2)
Предположение основано на том, что применение F-1 даст то же распределение, что и F1 на изображении, значения пикселов которого сдвинуты на единицу. Для обыкновенного изображения соотношение между группами не должно существенно меняться. Значительное расхождение между значениями свидетельствует о применении LSB-стеганографии для младших бит изображения.
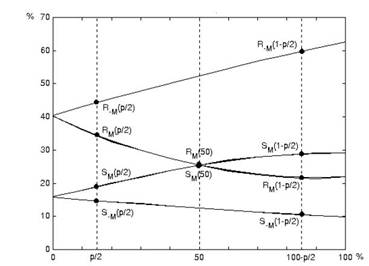
Рис. 1. RS-диаграмма типичного изображения
Рассмотрим изменения младших бит изображения при 100% перезаписи их битами сообщения. Внедрение случайного сообщения длиной, равной размеру изображения,приведет к тому, что 50% младших бит будут инвертированы. Это, в свою очередь сведет к нулю разность между значениями RM и SM. Однако на R-M и S-M внедрение сообщения будет влиять прямо противоположно, и разность этих величин будет пропорциональна степени заполненности контейнера, иными словами длине сообщения. На рис. 1 приведена RS-диаграмма для типичного изображения. На оси абсцисс расположено количество инвертированных бит x, искомая длина сообщения p, на оси ординат – относительные значения регулярных и сингулярных групп по отношению к общему числу групп изображения.
Предполагая, что в изображение внесено сообщение длиной p бит, и при этом 50% младших бит, использованных для записи, будут инвертированы, мы получаем значения статистик в точке p/2. Затем, если инвертировать все младшие биты изображения и пересчитать статистики, на диаграмме они будут соответствовать точкам кривых при x=100-p/2. Полной рандомизации младшей битовой плоскости соотвествует точка ½. Теперь, если принять p/2 за ноль, а 100-p/2 за единицу, а также использовать аппроксимацию кривых R-M и S-M прямыми а RM и SM параболами, можно вывести квадратное уравнение для нахождения координаты точки пересечения кривых RM и SM :
2(d1 + d0) x2 + (d−0 − d−1 − d1 − 3d0) x + d0 − d−0 =0, где
d0 = RM(p/2) − SM(p/2), d1 = RM(1−p/2) − SM(1−p/2),
d−0 = R−M(p/2) − S−M(p/2), d−1 = R−M(1−p/2) − S−M(1−p/2).
Затем, длина сообщения p вычисляется как p = x/(x−1/2). Таким образом, выходное значение длины является ответом для данного метода.
Данный метод был реализован программно и протестирован на множестве различных контейнеров и сообщений. В результате серии экспериментов были выявлены следующие особенности:
1. Метод обладает приемлемой точностью, в большинстве случаев оценка длины внедренного сообщения отличалась от истинного значения не более, чем на 5-10%.
2. RS-стегоанализ реагирует на естественный шум в изображениях, ограничивающий теоретически возможную точность определения длины сообщения, что дает на априори незаполненных контейнерах так называемое начальное смещение, положительное либо отрицательное. Начальное смещение выше у малых по размеру изображений вследствие малого числа регулярных и сингулярных групп. У изображений, полученных в результате обработки алгоритмами, снижающими избыточность, например JPEG, начальное смещение крайне мало.
3. Для сильно зашумленных изображений, помимо начального смещения, слабо отличаются значения статистик, полученных из разных функций флиппинга, таким образом, кривые пересекаются под малым углом, и точность метода снижается.
4. Метод демонстрирует более высокую точность при записи сообщения в случайно рассеянные пикселы, чем при записи в блоки подряд идущих пикселов. Увеличить точность в последнем случае можно, если применять метод к прямоугольной области изображения, а затем, постепенно сдвигая ее, локализовать расположение сообщения.
ЛИТЕРАТУРА
1. В.Г. Грибунин, И. Н. Оков, И. В. Туринцев. Цифровая стеганография. – М., Солон-пресс. 2002.
2. J. Friedrich, G. Miroslav, R. Du. Reliable Detection of LSB Steganography in Color and Grayscale Images. Binghampton, New York: SUNY, 2001.
3. J. Fridrich, R. Du, and L. Meng, “Steganalysis of LSB Encoding in Color Images”, ICME 2000, New York City.