Система взаимной проверки знаний (СВПЗ) с подключением арбитра предназначена для контроля уровня подготовленности группы учащихся. Взаимная проверка состоит в оценивании ответа учащегося несколькими его коллегами (самопроверки исключаются) [3]. По результатам оценок выдается заключение о состоянии каждого учащегося (знает, не знает). Для разрешения спорных ситуаций привлекается арбитр (преподаватель), то есть данная система позволяет перенести часть функций преподавателя на самих учащихся, уменьшая его нагрузку. Кроме того, для системы снимаются ограничения на класс тестовых задач (возможно использование открытых вопросов).
В основе модели системы взаимных проверок лежит принцип распределенного ядра, согласно которому диагностическое ядро системы заранее неизвестно и определяется на основе результатов взаимных проверок: в него включаются учащиеся, правильно ответившие на вопрос и правильно оценившие другие ответы (надежные учащиеся) [1,3].
Система работает следующим образом. Всем учащимся выдается одинаковая тестовая задача, каждый решает ее и передает посредством телекоммуникаций свое решение некоторому множеству абонентов (учащихся) для оценки, состав адресатов может меняться и заранее неизвестен посылающему [3]. Графически данная система представляется в виде орграфа O = (V,E), где V = {v1 , v2 , ... , vn} – множество учащихся, a E - множество дуг, указывающих на логические взаимосвязи между ними. Оценка aij ответов происходит по двухбалльной шкале (зачет-незачет): aij = 1, если абонент vi определяет ответ абонента vj как неправильный, и aij = 0 в противном случае. При этом считается, что если vi Î G, где G – множество хорошо подготовленных учащихся, то оценка (симптом) aij является надежной, в противном случае, vi Î F (F – множество неподготовленных учащихся), оценка aij – ненадежна. В случае, когда vi Î F, оценка aij – произвольна (0 или 1). Такая модель получила название ПМЧ-модели [1]. Совокупность всех симптомов aij образует синдром A=< aij > [1]. В графовой модели неподготовленные учащиеся интерпретируются как дефектные вершины.
Особенность использования этой модели для проверки знаний состоит в субъективизме взаимных оценок (в отличие от технических систем), что приводит к своеобразным ошибкам, которые получили название враждебных (byzantine) [2] или проблемы византийских генералов. В дальнейшем, будем называть вершину, которая соответствует учащемуся, неправильно решившему свою тестовую задачу, неисправной (Î F), а вершину, которая соответствует учащемуся, правильно решившему свою тестовую задачу, но неправильно оценившему ответы других учащихся, враждебной (Î BGP, от Byzantine Generals Problem). Совокупность неисправных и/или враждебных вершин назовём ненадёжными вершинами (учащимися).
В [3,4] рассмотрены алгоритмы нахождения ненадежных учащихся для полного и оптимального (Dd,t) графов. В случае полного графа имеет место большая нагрузка на каждого учащегося при любом количестве учащихся в группе, так как все вершины графа соединены между собой. В оптимальном графе с числом тестовых связей, равным nt (где n – количество вершин (учащихся) в системе; t – показатель диагностируемости графа, равный максимальному числу ненадежных вершин, при котором возможна однозначная и правильная расшифровка синдрома A), нагрузка на каждого учащегося возрастает прямо пропорционально росту числа обучаемых в группе. Чрезмерная загрузка каждого по проверке ответов приводит к утомляемости и, кроме того, негативно влияет на правильность оценивания. Таким образом, стоит задача уменьшения количества тестовых связей без уменьшения показателя диагностируемости графа. Проанализируем возможные подходы к решению данной задачи для оптимального графа.
1) В случае, когда число обучаемых в группе велико, на каждого учащегося при проверке ответов своих коллег ложится большая нагрузка, поэтому целесообразно разделить группу на подгруппы, где и проводить взаимные проверки. Такой подход уменьшит количество тестовых связей между вершинами. Однако и t также уменьшится. Проиллюстрируем это на примере группы, состоящей из n = 15 учащихся:
а) для оптимальной графовой модели имеем: t = 7 и каждому учащемуся нужно проверить по 7 ответов.
б) разделим группу на три подгруппы с n1 = n2 = n3 = 5 обучаемыми. В таком случае имеем для подгруппы: t = 2 и каждому учащемуся нужно проверить по 2 ответа. Следовательно, для всей группы t = 6, что ниже, чем для случая (а). Аналогичный результат получается при разделении группы на две подгруппы.
Рассмотренный подход применим в ситуации, когда заранее известно, что группа подготовлена хорошо.
2) Разделение множества всех вершин V на два подмножества H и L. К
|
|
|
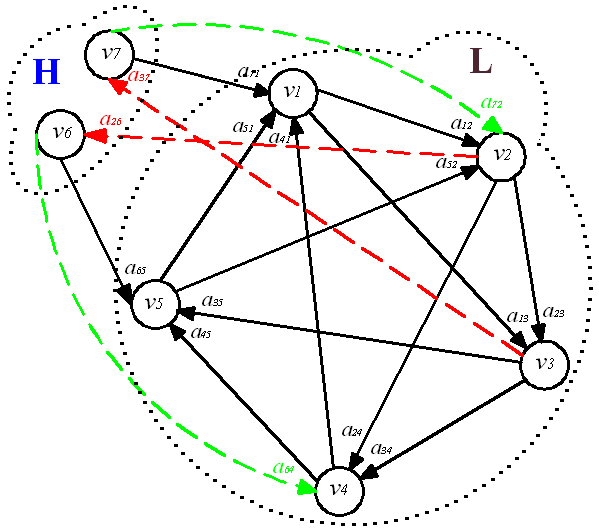
Рис. 1. – Разделение на 2 подмножества H и L |
|
|
|
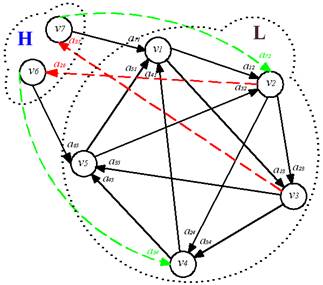
Рис. 2. – Число
тестовых связей равно |
подмножеству H относятся вершины, которые используются для контрольной проверки ответов других учащихся, к L – все остальные (рисунок 1). При таком подходе процедура проверки проводится в несколько этапов. Строятся оптимальная графовая модель между учащимися, входящими в подмножество L, а также по одной тестовой связи из вершин, входящих в подмножество H, в подмножество L (на рисунке 1 – a71, a65) и проводится расшифровка полученного синдрома. Затем, в случае необходимости (например, неоднозначность расшифровки), могут быть пущены дополнительные тестовые связи из вершин подмножества H (на рисунке 1 – a72, a64). Когда выяснено состояние вершин подмножества L, следует проверить правильность решения задания учащимися из подмножества H (на рисунке 1 – a37, a26). Таким образом, для группы, состоящей из n = 7 учащихся, число тестовых связей равно 16 (рисунок 1). Однако, при хорошей подготовленности группы количество дуг не должно превышать 14 (для оптимального графа с n = 7 это значение равно 21).
Стоит отметить, что применение рассмотренного подхода затруднено построением сложных алгоритмов, а также вероятным появлением случаев, когда расшифровать однозначно синдром не представляется возможным (случай, когда в графе несколько вершин подряд Î BGP).
3) Построение
графа взаимных проверок с числом тестовых связей, равным ![]() . Рассмотрим систему для n = 7
учащихся (рисунок 2). Необходимо, чтобы t = 3.
. Рассмотрим систему для n = 7
учащихся (рисунок 2). Необходимо, чтобы t = 3.
Проанализировав представленный граф, очевидно, что возможна неоднозначная либо однозначная, но неверная расшифровка синдрома в случаях, когда ненадежные вершины располагаются рядом. В таблице 1 приведены случаи возможной неверной расшифровки для примера рисунка 2.
|
Таблица 1 |
|||
|
№ случая |
Вершина i |
Вершина j |
Вершина k |
|
1 |
BGP |
BGP |
BGP |
|
2 |
BGP |
BGP |
F |
|
3 |
BGP |
F |
BGP |
|
4 |
BGP |
F |
F |
|
5 |
F |
BGP |
BGP |
|
6 |
F |
BGP |
F |
|
7 |
F |
F |
BGP |
|
8 |
F |
F |
F |
В целях недопущения неверной расшифровки необходимо предусмотреть средства, позволяющие выявить рассмотренные случаи, и разработать алгоритм подключения дополнительных тестовых связей для однозначного и правильного определения подготовленности учащихся. Такими средствами могут быть: а) нахождение характерных синдромов графа (в том числе для наилучшего и наихудшего случаев); б) определение приоритетности поиска данных синдромов; в) выявление общих для всех случаев особенностей (оценки, количество единиц для каждого случая); г) нахождение уникальности синдромов (т.е. уникальные отличия рассматриваемого случая от других для его дальнейшей однозначной идентификации) для каждого случая. Важно отметить, что в ситуации, когда обучаемого проверяют только учащиеся, признанные ненадежными, необходимо на данного учащегося пустить дополнительные тестовые связи либо подключить арбитра.
Рассмотренные подходы позволят уменьшить количество тестовых связей между учащимися, не уменьшая показатель диагностируемости графа. Кроме того, возможна их комбинация для более оптимальной организации взаимной проверки знаний.
В заключение отметим, что априорно неизвестно число ненадёжных учащихся в системе, поэтому для контроля следует подключать арбитра на наиболее информативную вершину, то есть вершину Î F, в которую входит наибольшее количество единичных дуг и которую тестируют обучаемые, признанные надежными.
ЛИТЕРАТУРА
1. Preparata F.P., Metze G., Chien R.T. On the Connection Assignement Problem of diagnosible systems // IEEE Trans. on Electronic Computers.- 1967, v. EC - 16.- P. 848-854.
2. Lamport L., Shostak R., Pease M. The Byzantine Generals Problem // ACM Transactions on Programming Languages and Systems, Vol. 4, No. 3, July 1982, Pages 382-401.
3. Афонин В.А., Пудов В.А. Проблема византийских генералов при расшифровки синдрома в системе взаимной проверки знаний с арбитром // Международный форум информатизации МФИ-2005. Труды международной научно-технической конференции «Информационные средства и технологии» – М.: Янус-К, 2005. – С. 80-83.
4. Афонин В.А., Пудов В.А. Методика выявления ненадежных учащихся в системе взаимной проверки знаний с арбитром // Международный форум информатизации МФИ-2005. Труды международной научно-технической конференции «Информационные средства и технологии» – М.: Янус-К, 2005. – С. 84-87.