BC/NW 2007, №2, (11) :2.1
СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПИРАМИДАЛЬНЫХ
СОРТИРОВОК
В.С.Зубов, В.В.Красков, И.В.Шевченко
(Москва, Московский энергетический институт (ТУ), Российская Федерация)
Множество алгоритмов пирамидальной сортировки в книгах и обзорных статьях по сортировке освещено неполно, а исследования их разрозненны, в лучшем случае касаются подмножеств алгоритмов [1]. На рис.1 показан класс пирамидальных сортировок, не требующих резерва памяти или требующих незначительного резерва, включая алгоритмы, опубликованные недавно (показаны на рис.1 выделением контуров).
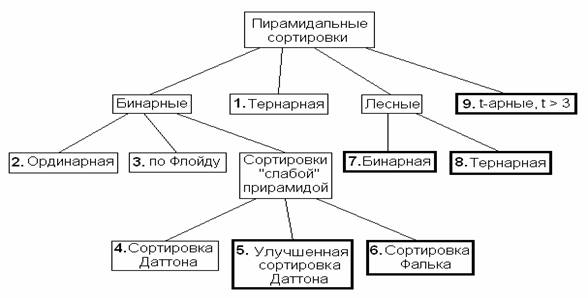
Рис. 1
Термином «ординарная» обозначена предложенная Дж. Уильямсом [1] сортировка, которая «единолично» представляет рассматриваемый класс в большинстве книг. Ее вариант «по Флойду» имеет ту особенность, что протаскивание ключей выполняется, начиная от уровня листьев, по предварительно намеченной трассе. Декларируемой целью этого изменения является сокращение среднего числа сравнений ключей.
Сортировка Даттона и ее модификации описаны и исследованы в [2], сортировка Фалька – в [3], бинарная лесная сортировка – в [4], t-арные пирамидальные сортировки исследованы в [5]. Ниже исследуемые алгоритмы обозначаются номерами, указанными на рис. 1. Транспозицией назовем изменение положения сортируемого элемента.
Сводя в один класс разработки разных авторов, поставим задачу обоснованного выбора алгоритмов для применения. Выбор зависит от ряда факторов; уделим главное внимание производительности сортировки и охарактеризуем области пространства параметров сортировки (размеров задачи), где тот или иной алгоритм опережает другие. Лучшие алгоритмы сравним с QuickSort [6] – общепризнанным «эталоном» производительности сортировки. Обозначим n число сортируемых элементов (записей), R – размер записи. Третьим параметром сортировки будет сложность ключа сортировки.
Таблица 1
|
№ |
Среднее число сравнений |
Среднее число перемещений P и обменов Q |
|
1 |
1.9∙( |
P
≈ 0.631∙( |
|
2 |
(2∙ |
P
≈ ( |
|
4 |
|
P
≈ n; Q ≈ 0.5∙ |
|
5 |
|
P
≈ |
|
6 |
|
P
≈ |
|
8 |
1.9∙( |
P
≈ 0.631∙ |
|
9 |
|
P
≈ ( |
Сначала сравним алгоритмы по числу операций. В табл. 1 приведены экспериментальные оценки среднего числа операций, полученные на кафедре математического моделирования МЭИ. Изучим оценки бинарных сортировок «2» – «6».
Алгоритм «6» явно проигрывает алгоритму «5», поэтому «6» исключаем. Алгоритм
«3» также не рассматриваем, поскольку в [5] выявлена его худшая временная
локальность. Именно она и дополнительные транспозиции не позволяют добиться
выигрыша во времени сортировки, а при малых n имеет
место даже проигрыш. Столь «дорогая» экономия числа сравнений не нужна.
При n > 100 алгоритм «2» выполняет почти вдвое больше
сравнений ключей, чем «4» или «5». С уменьшением n разница в
числе сравнений сокращается, исчезая при n = 4. По
затратам на транспозиции «2» и «4» различаются мало, однако алгоритм «5»
получает преимущество перед ними при увеличении R.
Правомерен вывод о том, что при сложном ключе или сложных преобразованиях
ключей перед сравнениями предпочтительны алгоритмы «4» и «5», а при увеличении
размера записи следует выбирать только «5».
Неопределенной остается ситуация сортировки простых ключей (не записей), когда ни время сравнений, ни время транспозиций не доминирует в общих затратах. Здесь многое зависит от сложности вспомогательных действий, например, действий в управляющем дереве, которые присутствуют в «4» – «6», регулярных действий по восстановлению пирамиды. Возможности сократить вспомогательные действия без особого усложнения алгоритмов найдены: в «2» устранены приблизительно n log 2 n проверок индекса, а в «5» – примерно 0,5 n log2 n обращений к управляющему дереву. Машинный эксперимент, безусловно необходимый в случае сортировки простых ключей, дает следующий итог: алгоритм «2» быстрее «4» и «5» и является серьезным конкурентом QuickSort.
Все рассмотренные сортировки, кроме «2», выполняют примерно на 40% меньше сравнений ключей, чем QuickSort, заметно проигрывая QuickSort по числу транспозиций. Исследуем пути преодоления этого недостатка пирамидальных сортировок.
Аналитически доказано и подтверждено экспериментально, что тернарная сортировка «1» затрачивает примерно на 5 % меньше сравнений, чем «2», а длина трасс протаскивания ключа в ней в среднем меньше в log2n/log3n раз. Примерно во столько же раз меньше и перемещений. Однако выгоднее использовать не одну пирамиду, а лес из s тернарных пирамид, построенный по тому же принципу, что бинарный лес в [4]. Дело в том, что выбор наибольшего из s корневых элементов пирамид, выполняемый простым перебором, затрачивает меньше сравнений, чем выбор такого элемента в пирамиде, если 1 < s < 7. Существенно то, что при простом переборе нет перемещений. Итак, не увеличивая число сравнений, можем укоротить трассы протаскивания ключей и добиться преимущества перед бинарными сортировками «2» – «6».
Оценки числа действий, данные в табл. 1, выделяют «8» как перспективный алгоритм. Ситуация не однозначна: меньшее число сравнений ключей в «5» заставляют предпочесть «5» при сортировке сложных ключей и небольшой длине записей. Напротив, при большой длине сортируемых записей откажемся не только от «5», но и от «8», выбирая «9». Причина пояснена ниже.
Сортировка t-арной пирамидой (t > 3), увеличивая число сравнений ключей с ростом параметра t, сокращает число транспозиций (пропорционально уменьшению высоты пирамиды). Как показали исследования [4], правильный выбор значения t при больших (сотни байтов) размерах записей и, что особенно важно, больших n (сотни тысяч и более записей) значительно уменьшает и число промахов мимо кэша. Сортировка t-арной пирамидой становится в один ряд с сортировкой QuickSort, как известно, отличающейся хорошей локальностью.
Итак, предварительный анализ выделяет улучшенную сортировку Даттона, лесную тернарную сортировку, сортировку t-арной пирамидой и QuickSort как достаточный набор алгоритмов для обеспечения наибольшей производительности в большей части пространства параметров сортировки.
Нагляднее представить области этого пространства, где один из алгоритмов является самым производительным, можно с помощью серии графиков. На рис. 2 – 5 даны примеры графиков. Имитируя время сортировки, на оси ординат отложена взвешенная сумма среднего числа сравнений ключей и среднего числа транспозиций, определяемых формулами табл. 1. Вес сравнения обозначим Mc, вес транспозиции – Mт.
Для рис. 2 взяты Mc = 50, Mт = 1; это случай, когда используются либо весьма сложные ключи, либо сложно преобразуемые перед сравнением. Именно эта область представлена в [2] для выгодного освещения предлагаемых в [2] алгоритмов. Число операций в «4» и «5» практически совпадает.
Для рис. 3 взяты Mc = 1, Mт = 50; это случай, когда сортируются записи немалого размера по несложному ключу. В этом примере виден недостаток способа, требующего скрупулезного учета относительной сложности операций. При построении рис.3 обмен приравняли двум перемещениям. Если бы сложность обмена оценили выше, график «4» поднялся бы, т.е. выигрыш алгоритма «5» стал заметнее, что соответствует реальности.
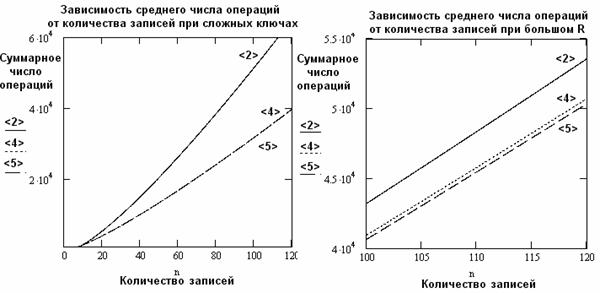
Рис. 2 Рис. 3
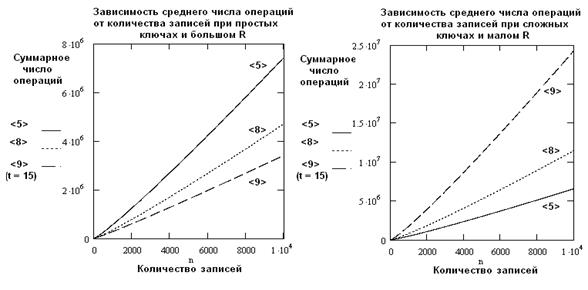
Рис. 4 Рис. 5
Рис. 4 показывает значительное преимущество t-арной сортировки над конкурентами при большом размере записей и простом ключе сортировки (Mс= 1, Mт = 50); рис. 5 представляет обратную ситуацию (Mс= 50, Mт = 1). Если при построении рис. 5 взять параметр t = 3-4, график «9» пройдет лишь немногим выше графика «8», хотя проигрыш алгоритму «5» по-прежнему будет значительным.
Машинный эксперимент, проведенный для статистической оценки средних затрат времени, подтвердил выводы, сделанные в ходе исследования операций, выполняемых при сортировке. Для более точной оценки времени сортировки проводятся исследования локальности пирамидальных сортировок.
Новые разработки пирамидальных сортировок, выполненные на кафедре математического моделирования и кафедре прикладной математики МЭИ, подтверждают высокий статус пирамидальной сортировки, отмеченный в [5]. Имея высокую производительность, она отличается стабильным временем сортировки, не требует резерва памяти или использует небольшой резерв.
ЛИТЕРАТУРА
1.Williams J.V.J. HeapSort (Algorithm 232). Comm.ACM, 7. № 6 (1964). 347-348.
2.Edelkamp S., Stiegeler P. Implementing HeapSort with nlog-0.9n and QuickSort with nlog-0.9n Comparisons. Albert-Ludving-Universitat, Freiburg.
3.Зубов В.С., Фальк В.Н. Новый алгоритм быстрой сортировки выбором //Вестник МЭИ. 2006. №6. С. 62-68.
4.Зубов В.С. Справочник программиста. Базовые методы решения графовых задач и сортировки. – М.: Информационно-издательский дом «Филинъ», 1999. -245 с.
5.Зубов В.С., Шевченко И.В. О статусе пирамидальной сортировки // Вестник МЭИ. 2005. №3. С.89.
6.Hoare C.A.R. Quicksort. Comp.J., 5. № 1 (1962). 10-15.