BC/NW 2007, №2, (11) :3.1
ВЫБОР ПРИОРИТЕТНЫХ ПОЛЬЗОВАТЕЛЕЙ ДЛЯ УПРАВЛЕНИЯ ПРОИЗВОДИТЕЛЬНОСТЬЮ КОРПОРАТИВНОЙ ВЫЧИСЛИТЕЛЬНОЙ СЕТИ
Л.И. Абросимов, Лазар Матип Эссунга
(Москва, Московский энергетический институт (ТУ), Россия)
Современные корпоративные вычислительные сети (КВС) предостав-ляют свои информационно-вычислительные ресурсы большому количест-ву пользователей. Требования пользователей к скорости выполнения реша-емых задач – различны и определяются их ролью в технологическом процессе корпорации. Поэтому каждый пользователь предъявляет свои требования к производительности КВС.
Администратор КВС имеет права и технические возможности предос-тавлять пользователям приоритеты обслуживания. Однако, в сетевых протоколах есть механизм обработки приоритетных транзанкций, но нет методов выбора количества приоритетных пользователей.
Задача выбора приоритетных пользователей, работающих в диалоговом режиме, состоит в том, чтобы определить количество приоритетных пользователей, для каждого из которых выполняется допустимое время реакции КВС.
В основу методики определения допустимого количества nqА приоритетных пользователей положен метод контуров [1].
Исходными данными для решения поставленной задачи
является структура S КВС, замкнутые контура qi 
Q, описывающие диалоговый режим. В каждом контуре qi циркулируют
nq транзакций, из которых nqА
могут быть приоритетными (nqA 
nq).
Устройства КВС (хостмашины, каналы и рабочие станции) обслуживают транзакции с
интенсивностью 
.
Время tq реакции для транзакций контура qi не
должно превышать допустимое время 
.
Производительность КВС, в соответствии с [1,2], оценивается количеством транзакций, которые обслуживаются ресурсами КВС в единицу времени. Транзакция – это задание на обслуживание, которое в канале связи имеет форму пакета данных, измеряемого в байтах, а в обслуживающем компьютере – форму задания, измеряемого количеством вычислительных операций, т.к. КВС обслуживает разные типы транзакции. Решение задачи выбора количества приоритетных пользовате-лей выполняется поэтапно, в соответствии с методом контуров [1].
1. По структуре S и заданным контурам Q строится графовая модель.
2. В соответствии с графовой моделью составляется система нелинейных уравнений.
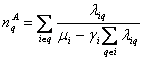(1)
3. Для каждого контура, обрабатывющего приоритетные
транзакции, составляется функциональное уравнение, в котором интенсивность λi,q
потока транзакций зависит от
допустимого времени , интенсивности 
обслуживания и количества nqА
приоритетных транзакций контура qi
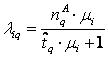(2)
4. Решая систему уравнений, включающую соотношения (1) и (2), получаем требуемые значения количества nqА приоритетных транзакций для каждого контура q, которое равно количеству приоритетных пользователей.
Рассмотрим в качестве примера определение nqА для КВС, структура которой представлена на рис. 1.
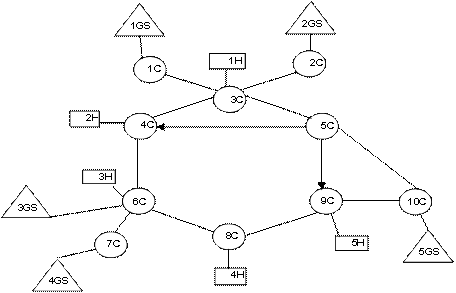
Рис. 1 Структура исследуемой КВС
Структура КВС содержит: серверы (1H, 2H, 3H, 4H, 5H),
которые че-рез каналы связи и коммуникационные контроллеры (1С – 10С)
обслужи-вают в диалоговом режиме 300 рабочих станций (1S – 300S),
которые объеденены в пять групп. (1GS – 5GS), 1GS
имеет в своем составе 40 рабочих станций, 2GS -- 60 рабочих
станций, 3GS -- 80 рабочих станций, 4GS -- 60 рабочих
станций, 5GS -- 60 рабочих станций. Cерверы имеют
интенсивности обслуживания µ1 =60 1/s, каналы связи
µ2 =40 1/s, рабочие станции µ3 =0,333 1/s. В
сети функционируют 5 контуров. Допустимое время варьируется в интервале 1 – 3 секунды.
Требуется определить допустимое количество nqА приоритетных пользователей.
В соответствии с предложенной методикой построена графовая модель, представленная на рис. 2.
Рис. 2 Графовая модель исследуемой КВС
Для каждого контура q составляются нелинейные уравнения. Пример уравнения для q=1 представлен соотношением (3).
(3)
Результаты совместного решения системы уравнений (3) и (2) для исследуемой КВС представлены в таблице 1
Таблица 1. Изменение количества приоритетных пользователей
от допустимого времени реакции для q=1/
|
Допустимое время реакции приоритетных. пользователей |
Количество приоритетных пользователей |
Время реакции не приоритетных пользователей. |
|
1,0 с |
4 |
6,33 с |
|
1,5 с |
7 |
11,99 с |
|
2,0 с |
9 |
19,32c |
Первый контур исследуемой КВС включает в свой состав 40 пользова-телей. При выделении из этого состава 4-х приоритетных пользователей, которым должно быть обеспечено время реакции 1,0 с, время реакции остальных 36-ти пользователей составляет 6,33 с. Из таблицы 1 видно, что ресурсы исследуемой КВС позволяют обеспечить приоритетное обслуживание с допустимым временем реакции 1,5 с 7-ми пользователям, а с временем 2,0 с –9-ти пользователям.
Предложенная методика расчета позволяет учитывать взаимное влияние приоритетных пользователей, входящих в разные контура, если они используют общие ресурсы (серверы или каналы связи).
На рис. 3 представлены зависимости, которые показывают нелинейный рост количества приоритетных пользователей в зависимости от требуемого времени реакции приоритетных пользователей. Следует отметить, что расчеты ведутся для стационарных режимов, при этом количество приоритетных пользователей и время реакции представляют собой усредненные величины.
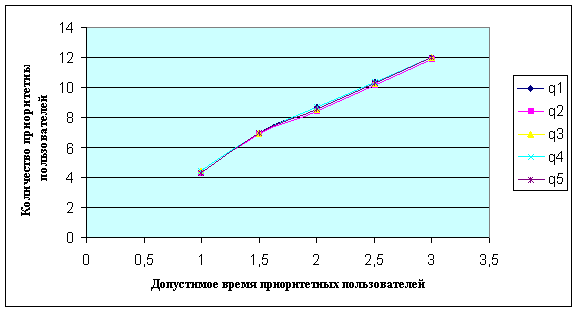
Рис. 3 Изменение количества приоритетных пользователей КВС от допустимого времени реакции для пяти контуров.
Предложенная методика ориентирована на решение задач реальной размерности КВС, которые имеют в своем составе 500 и более устройств.
Трудоемкость решения задач в первую очередь определяется количеством пользователей и связанным с ними количеством контуров.
Существенным ограничением для широкого применения предложен-ной методики является проблема определения интенсивности обслужива-ния транзакций, над решением этой проблемы авторы введут работу.
Литература
1. Абросимов Л.И. Анализ и проетирование вычислительных сетей: учебное пособие – М.:, Изд-во МЭИ. 2000. – 52с
2. Абросимов Л.И. Основные положения теории производительности вычислительных сетей / Вестник МЭИ – 2001 - №4 – с. 70 - 75
3. Лазар Матип Эссунга, Абросимов Л.И Задачи управления производительностью корпоративных вычислительных сетей ХIII Международная научно-техническая конференция студентов и аспирантов РАДИОЭЛЕКТРОНИКА, ЭЛЕКТРОТЕХНИКА И ЭНЕРГЕТИКА 1-2 марта 2007 г. тезисы докладов Изд-во МЭИ, том 1. 412-413с