BC/NW 2007, №2, (11) :4.2

МОДЕЛЬ ОЦЕНКИ ЭФФЕКТИВНОСТИ ТЕСТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

Ермаков А. А.

(Москва, МГТУ «СТАНКИН Российская Федерация)

С тех пор как в середине XX века в науке и технике началось активное использование ЭВМ, компьютеры занимают все большее место в нашей жизни. Компьютерная революция породила такое быстрое развитие технологий, какого мир еще не видел за все время его существования. Сегодня наше удобство, комфорт, а подчас и жизнь зависят от качества работы компьютеров. Все сколько-нибудь значимые отрасли экономики: промышленность, энергетика, телекоммуникации, финансы, транспорт не могут управляться без помощи компьютеров.

Сложность устройства компьютерных контроллеров за последние десятилетия выросла многократно. Например, программное обеспечение шаттлов включает в себя более 500,000 строк кода в бортовых ЭВМ и более 3,5 миллионов строк в наземных контролирующих системах [1].

Ошибки в программном обеспечении могут дорого обойтись экономике. Именно поэтому очень большое значение имеет качество программного обеспечения. В данной статье рассматриваются вопросы оценки качества программного обеспечения и прогнозирования результатов его эксплуатации в реальных условиях на базе разработанной математической модели эксплуатирования ПО.

К сожалению, в настоящее время отсутствуют общепринятые методики, позволяющие оценить качество программного продукта после тестирования.

С первого взгляда проблема кажется тривиальной: достаточно собрать статистику эксплуатации ПО, например, за год и получить ответ. Но как можно еще на этапе тестирования определить, что ПО уже достигло требуемого уровня надежности и дальнейшее тестирование экономически нецелесообразно? Как можно оценить эффективность тестирования еще до выхода продукта?

Ricky W. Butler и George B. Finelli в своем исследовании [2] показали, как можно оценить время тестирования ПО для достижения заданного уровня надежности. Ответ был неутешительным: для высоконадежных программ (вероятность отказа ) время тестирования может составить сотни тысяч лет.

Но при этом исследователи не дали ответа на вопрос, сколько ошибок осталось в протестированном ПО, и как они будут проявляться в процессе эксплуатации.

Разработанная модель лишена этого недостатка.

Исходными данными для данной модели служат результаты тестирования ПО. Сложность заключается в том, что обнаруженные ошибки делятся по степени критичности и степени влияния на другие программные модули, поэтому, количество найденных ошибок необходимо взвесить соответствующими коэффициентами.

Модуль, в котором обнаружена ошибка, может по-разному влиять на работу комплекса в целом, поэтому необходимо использовать дополнительные коэффициенты: модуль влияет на функционирование ядра, модуль влияет на функционирование других модулей (не всех), модуль не влияет на функционирование системы в целом.

Таким образом количество ошибок, найденных за определенный период можно подсчитать по следующей формуле:

(1)

Здесь C_ош - это количество ошибок определенной критичности определенного модуля, K_кр - коэффициент критичности, K_мод- коэффициент использования модуля.

Итоговая таблица выглядит так:

Время тестирования (в неделях)	Количество ошибок (нарастающим итогом)
1
2
n

Известно, что по мере тестирования вероятность обнаружения ошибки уменьшается. На это, в частности, указывал Miller [4]. Для определения количества найденных ошибок из эмпирических соображений о процессе тестирования и эксплуатации ПО была выбрана аппроксимирующая функция. Из статистических исследований было установлено, что наилучшим образом подходит функция вида

(2)

При этом, очевидно, коэффициент C₀ покажет общее количество ошибок в программном комплексе, т.к. понятно, что данная функция является убывающей.

Для проверки правильности выбора функции использовался метод линеаризации данных. Как известно, суть его заключается в том, что если функция, показывающая зависимость между x и y выбрана верно, то зависимость можно свести к линейной. Действительно, если мы прологарифмируем левую и правую части нашего выражения (2), то получим следующее:

ln y = ln(C₀+C₁C₂x) (3),

или, приближенно:

ln y ~ ln x (4)

Нетрудно заметить, что величины ln y и ln x оказываются связанными линейной зависимостью. Если экспериментальные данные, т.е. пары точек (x_i, y_i) действительно связаны зависимостью (2), то согласно (4) график зависимости ln y_i от ln x_i должен быть близок к линейному. Этот вывод подтверждается графиком 1.

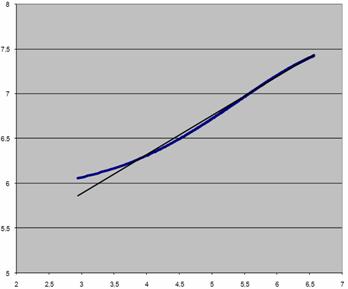
График 1. Зависимость ln y_i от ln x_i

Таким образом мы доказали адекватность данной модели.

Для определения значений коэффициентов C₀, C₁, C₂ можно воспользоваться методом наименьших квадратов. Как известно, суть его заключается в минимизации суммы квадратов разниц теоретического и фактического значений функции в известных точках.

Исходя из выражения (2), получаем следующее:

(5)

Для того, чтобы найти ее минимум, нужно приравнять к нулю ее частные производные по переменным C₀, C₁, C₂.

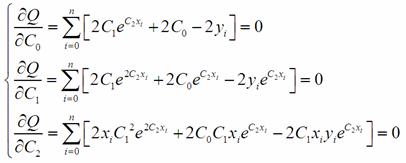(6)

Для переменных C₀, C₁ аналитические выражения выглядят следующим образом:

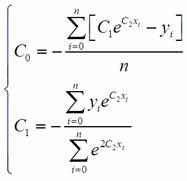(7)

Для C₂ получать аналитическое выражение нецелесообразно из-за его большой сложности, для его нахождения можно подставить в третье уравнение значения C₀, C₁, после чего решить его одним из итерационных методов, например, методом дихотомии.

Для проверки данной модели использовался релиз M продукта N.

Таблицу с данными по количеству ошибок не приводим из-за ее размеров.

Построив график на имеющихся данных тестирования программного комплекса N в течение нескольких лет, получили следующий график:

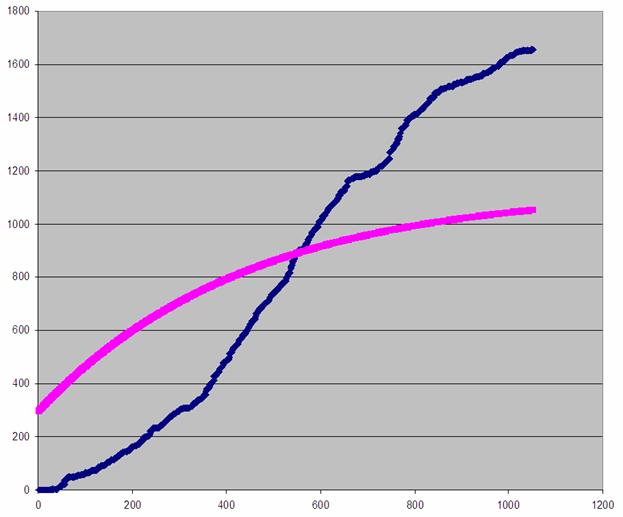
График 2. Количество найденных ошибок в программном комплексе N от времени тестирования

Из данного графика видно, что предложенная модель имеет мало общего с реальностью. Как же могло так получиться? Ответов несколько, и все они лежат в области, не поддающейся математическому моделированию. Прежде всего, это особенности принятой в компании-разработчике технологии тестирования, когда продукт сначала проходит предварительное тестирование в Службе разработки и Инженерном секторе при составлении конфигураций, затем продукт поступает в модульное тестирование и лишь спустя значительный промежуток времени в комплексное. По сути, время выделяется на предварительное и модульное тестирование по остаточному принципу (так как одновременно завершается комплексное тестирование и внедрение предыдущего релиза), в то же время сам релиз еще очень сырой, отсюда и значительный рост количества найденных ошибок. Время идет, на работу над релизом выделяется все больше и больше ресурсов, в то же время самые легковоспроизводимые ошибки уже исправлены (поскольку их нахождение не требует больших затрат ресурсов). Наступает период стабилизации, когда разработанная модель адекватна реальности. Он продолжается до окончания жизненного цикла релиза.

Правоту этих выводов подтверждает график 3.

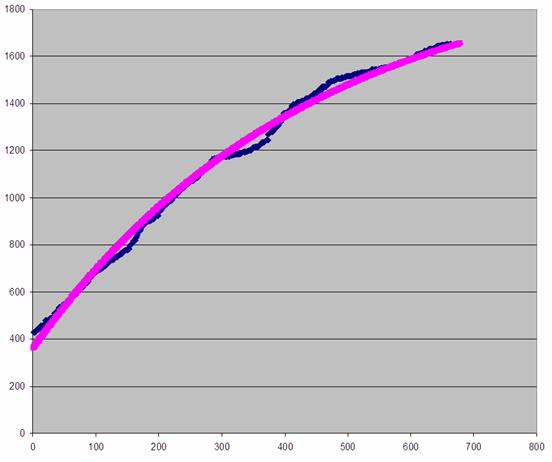
График 3. Количество найденных ошибок в программном комплексе N от времени тестирования (фрагмент)

Видно, что в последних точках графики теоретический и реальный практически совпали, что означает, что теоретическую кривую можно использовать для прогнозирования количества найденных ошибок в будущем.

Как видно, наша модель довольно точно отражает процесс роста количества найденных ошибок. Из полученного результата видно, что остались необнаруженными порядка 350 ошибок. Это отнюдь не означает, что все они проявят себя на этапе эксплуатации, часть их никогда не будет обнаружена по причине очень значительных трудозатрат или весьма экзотических сценариев проявления. Для более точного прогноза обратимся к графику 4.

Если мы продлим его до окончания жизненного цикла релиза, то получим следующий результат (см. график 3). При этом мы считаем, что продукт эксплуатируется 2 года, при этом не стоит забывать, что внедрение начинается еще до завершения этапа комплексного тестирования.

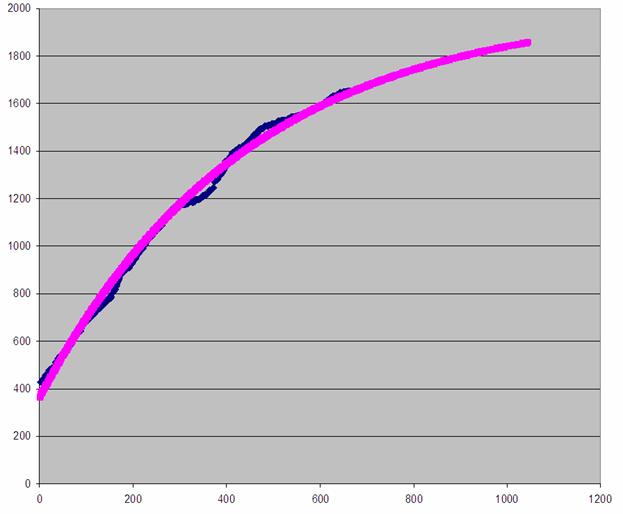
График 4. Количество найденных ошибок в программном комплексе N от времени тестирования (прогноз на 2007 г.)

Таким образом, в текущем году может быть обнаружено около 200 ошибок (в сумме, взвешенных коэффициентами). Между тем, эффективность тестирования как отношение количества найденных ошибок к общему количеству составляет:

.

Это весьма достойный результат, учитывая, что тестирование выполняется методом черного ящика.

Сложность программного обеспечения растет с каждым днем, соответственно увеличивается и время его тестирования. Между тем экономические реалии требуют скорейшего вывода на рынок нового продукта, что вступает в противоречие с идеей тщательного тестирования продукта. Разработанная модель позволяет найти разумный компромисс: тестирование осуществляется ровно до того момента, как количество ошибок придет в соответствие техническому заданию, что позволит избежать лишних затрат.

Более того, построенная модель позволяет предсказать поведение программного комплекса в процессе эксплуатации.

Таким образом, мы получаем возможность определить количество требуемых ресурсов для разработки, тестирования и сопровождения разработанного ПО.

Литература

Michael R. Lyu. “The need for reliable software”, AT&T Bell Laboratories

Ricky W. Butler and George B. Finelli, “The Infeasibility of Quantifying the Reliability of Life-Critical Real-Time Software”, NASA Research Center, 1993.

D. Miller, “Making statistical inferences about software reliability”, NASA Contractor Report 4197, Nov. 1988.

P. A. Keiller and D. R. Miller, “On the use and the performance of software reliability growth models”, Reliability Engineering and System Safety, pp. 95-117, 1991.