BC/NW 2007, №2, (11) :7.2

о возможности обобщения параллельной модулярной арифметики

для работы с двоичными дробями.

Ш. А.Оцоков

(Москва, Московский Энергетический Институт (ТУ), Россия)

Эффективность решения многих вычислительных задач на ЭВМ зависит от быстродействия и точности вычислений с плавающей точкой. Быстродействие вычислений с плавающей точкой ограничивается необходимостью учета межразрядных переносов, возникающих при сложении, вычитании и умножении чисел.

В модулярной системе счисления (МСС) арифметические выполняются без переносов по нескольким выбранным модулям. Благодаря чему существует возможность ускорения вычислений с многоразрядными числами за счет их распараллеливания по нескольким модулям [1]. Однако, МСС ориентирована на проведение целочисленных вычислений и поэтому применяется при решении специализированных задач цифровой обработки сигналов, в помехозащищенном кодировании и др.

Цель настоящей работы обобщить арифметику МСС для работы с двоичными дробями и тем самым расширить область её применения. Для описания предложенных алгоритмов работы с дробями рассмотрим представление двоичных дробей в МСС.

Известно, что любую двоичную дробь можно представить в следующем виде:

, (1)

где

целая часть числа, некратная двум.
дробная часть числа, .

Пусть произведение простых модулей МСС, такое, что

, (2)

где

- максимально возможное значение.

Условие (2) обеспечивает представление отрицательных чисел в МСС.

В МСС число по модулю будет иметь следующий вид:

Восстановить число по его модулярному представлению при условии (2) можно, если:

- определить знаменатель .

- умножить знаменатель на по модулю и получить числитель .

Определение знаменателя

В процессе сложения, вычитания и умножения двоичных дробей возможны сокращения числителя и знаменателя на числа, которые являются степенями двойки. Для их обнаружения нужна проверка делимости числителя на числа вида 2^t, (t>=1) Необходимо, чтобы эта проверка осуществлялась как можно быстрее, т.к. в противном случае применение модулярной арифметики не даст какого-либо эффекта ускорения вычислений.

Один из эффективных способов обнаружения делимости числителя – применение арифметики кодов Гензеля по модулю два [2]. Вычисления проводятся с двоичными дробями в модулярной арифметике и в кодах Гензеля параллельно и независимо друг от друга. Делимость числителя проверяется с помощью свойства кодов Гензеля: если в мантиссе кода Гензеля t младших разрядов нулевые, то числитель имеет делитель 2^t . Коды Гензеля характеризуются двумя параметрами: модулем и длиной мантиссы. Так как вычисления проводятся с двоичными дробями, то модуль должен быть равным двум, если код Гензеля имеет s-разрядную мантиссу, то это означает, что может обнаружен делитель числителя вида 2^t, где (t<=s). Если в процессе выполнения арифметических операций с двоичными дробями получен код Гензеля с нулевой мантиссой, тогда необходимы преобразование предыдущего результата арифметических операций из МСС в дробь, коррекция соответствующего ему кода Гензеля, увеличение длины мантиссы.

Предложен следующий формат представления двоичных дробей
(рис 1).

m1

… mN

H

Рис. 1. Формат представления двоичной дроби

На рис.1 поля m₁, … m_N – это значения в МСС по модулям
m₁, … m_N соответственно, а поле Н – это код Гензеля числа .

Переполнение, округление в МСС

Неравенство (2) определяет диапазон представимых двоичных дробей в МСС. Если в результате вычислений получена дробь, выходящая за пределы допустимого диапазона, то возникает ошибка переполнения и необходимо округление результата. Один из известных способов обнаружения переполнения в модулярных вычислениях основан на методе нулевизации, разработанный Акушским И.Я [1]. Для его реализации необходимо выбрать дополнительный модуль m_N+1 удовлетворяющий условию:

( m₁ ×…× m_N mod m_N+1 )^-1 mod m_N+1 º 1.

Увеличение количества модулей с одной стороны дает возможность расширить диапазон представления двоичных дробей и уменьшить количество возможных округлений в процессе вычислений, с другой стороны при заданном диапазоне уменьшить величину самих модулей. Последнее можно использовать для ускорения вычислений путем совмещения модульных операций. Если модули невелики можно заранее вычислить результаты выполнения последовательности
2-х арифметических операций для всевозможных входных данных и за один такт их выполнить. Рассмотрим правило округления двоичных дробей.

Правило округления числа А

1. По коду Гензеля числа А (поле Н рисунок 1) определение знаменателя А и преобразование его в МСС

2. Умножение модулярного представления числа А ( поля m₁, … m_N рис. 1) на результат в п.1

3. Преобразование модулярного представления числа А ( поля m₁, … m_N рис. 1) в позиционную систему счисления.

4. Округления результата, полученного в п.3. до ближайшего целого, принадлежащему допустимому диапазону представления двоичных дробей.

Округление в МСС отличается от округления в позиционной системе счисления, тремя дополнительными операциями (пункт 1-3). Существуют различные способы ускорения их выполнения, поэтому можно считать, что время округления в МСС не сильно отличается от времени округления в ПСС.

Для уменьшения количества округлений в процессе вычислений необходимо увеличить величину каждого из модулей или их количество в соответствие с неравенством:

m₁ ×…× m_N > (K max)^V,

где

V - характеризует параметр, показывающий какое количество арифметических операций умножения можно провести без округлений.

Модель вычислений с двоичными дробями представлена на рис.2.

В соответствии с этой моделью исходные данные, решаемой задачи – Х, преобразуются в СОК по заданным модулям р₁,…,р_N и коды Гензеля. Далее проводятся вычисления по правилам модулярной арифметики и кодов Гензеля. После выполнения каждых арифметических операций результат округляется. Если в ходе вычислений возникает ошибка переполнения, т.е. , то результат корректируется и вычисления продолжаются. Конечные результаты вычислений преобразуются в двоичные дроби Y.

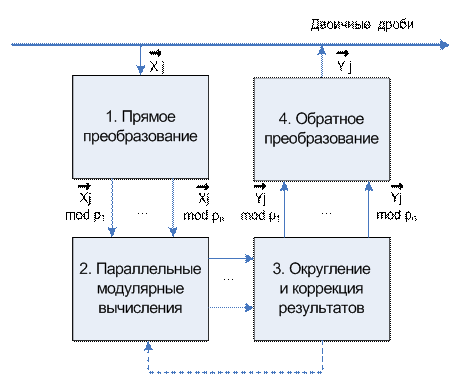
Рис. 2 . Модель вычислений с двоичными дробями.

Деление двоичных дробей сводится к преобразованию в позиционную систему счисления делителя, нахождению его обратного, преобразования в МСС и умножения на делимое. Недостатком МСС является сложность деления чисел. Поэтому модулярные вычислений с двоичными дробями будут эффективны в задачах с минимальным количеством делений. В целях ускорения целесообразно заменять операцию деления где это возможно на операцию умножения, например, если деление производится на некоторые заданные константы.

Ниже представлены правила сложения/вычитания и умножения двоичных дробей в МСС.

Сложение / вычитание

Входные данные:

Х₁ mod m₁, Х₁ mod m ₂, …, Х₁ mod m _N

Х₂ mod m ₁, Х₂ mod m ₂, …, Х₂ mod m _N

H(2,r, Х₁ ), H(2,r, Х₂ ) – коды Гензеля чисел Х₁ и Х₂

Выходные данные:

Сумма /разность чисел Y₁= Х₁ ± Х₂ .

Y₁ mod m ₁, Y₁ mod m ₂, …, Y₁ mod m _N

H(2,r, Y₁ ) – код Гензеля Y₁ суммы/разности чисел Х₁ и Х₂

1. Определяется сумма/разность H(2,r, Y₁ ) = H(2,r, Х₁ ) ± H(2,r, Х₂ )
2. Определяются значения выражений Y₁ как сумма/разность чисел Х₁ и Х₂ по модулям m₁, m ₂, …, m _N

Умножение

Входные данные:

Х₁ mod P₁, Х₁ mod P₂, …, Х₁ mod P_N

Х₂ mod P₁, Х₂ mod P₂, …, Х₂ mod P_N

H(2,r, Х₁ ), H(2,r, Х₂ ) – коды Гензеля чисел Х₁ и Х₂

Выходные данные:

Произведение чисел Y₁= Х₁ ± Х₂ .

Y₁ mod P₁, Y₁ mod P₂, …, Y₁ mod P_N

H(2,r, Y₁ ) – код Гензеля Y₁ произведения чисел Х₁ и Х₂

1. Определяется произведение H(2,r, Y₁ ) = H(2,r, Х₁ )* H(2,r, Х₂ )

2. Определяются значения выражений Y₁ как произведение чисел Х₁ и Х₂ по модулям m₁, m ₂, …, m _N

ВЫВОДЫ

В статье обобщены алгоритмы многомодульной арифметики для работы с двоичными дробями.

Перспективным направлением дальнейшей работы является исследование возможностей реализации методов решения дифференциальных уравнений Рунге-Кутта, Эйлера и других численных методов на основе многомодульной арифметики двоичных дробей на процессорах многоядерной архитектуры.

Литература

1. Акушский И.Я, Юдицкий. Д.И. Машинная арифметика системы остаточнх классов. – М.: 1968.

2. Грегори Р., Кришнамурти Е. Безошибочные вычисления. Методы и приложения: Пер. с англ. – М.: Мир, 1998.