BC/NW 2008, №2 (13): 10.1

СТРУКТУРНАЯ ИНФОРМАТИКА: НОВЫЕ ВИДЫ ОТНОШЕНИЙ ЭКВИВАЛЕНТНОСТИ ГРАФОВ

Кохов В.А.

(Москва, Московский энергетический институт (ТУ), Россия)

Структурная информатика – новый раздел информатики актуальный для изучения студентами в университетах [1]. В докладе предложен метод построения структурных инвариантов графов, впервые позволяющих определять стратифицированную систему отношений эквивалентности графов, основанную на учете сходства расположения их фрагментов. Данный метод программно реализован в АСНИ «GMW» и используется в учебном процессе МЭИ, позволяя студентам изучать новые подходы к классификации графов, ставить и решать сложные задачи на стыке теории графов и теории групп.

Определим класс граф-моделей, позволяющих характеризовать сходство расположения фрагментов в графе G=(V,E) и формировать систему новых видов отношений эквивалентности графов, впервые основанную на сходстве расположения фрагментов.

Пусть M (M^l ) - множество обыкновенных (помеченных) графов,

множество всех собственных фрагментов (помеченных фрагментов) графа, а

множество помеченных фрагментов типа t, j - номер фрагмента, rt - число фрагментов типа t, T - число типов фрагментов.

Под графом отношений фрагментов (g-моделью) графа G будем понимать двудольный граф с весами на вершинах и рёбрах вида:

определяемый параметрами sr, B_L, B_R, E_L, E_R, где:

1. sr – бинарное отношение на множестве M^l, то есть

2. B_L – базис левой доли (множество фрагментов левой доли);

3. B_R – базис правой доли (множество фрагментов правой доли);

4. E_L – функция, определяющая тип вложения фрагментов из B_L в граф G

5. E_R – функция, определяющая тип вложения фрагментов из B_R в граф G

6. V_L – множество вершин левой доли (вершина vÎV_L соответствует одному из помеченных фрагментов – канонических вложений элементов B_L в G);

7. V_R – множество вершин правой доли (вершина vÎV_R соответствует одному из помеченных фрагментов – канонических вложений элементов B_R в граф G);

8. E – множество рёбер:

9. WV_L – множество весов вершин левой доли

10. w_L – функция, сопоставляющая вершинам V_L их веса

11. WV_R – множество весов вершин правой доли

12. w_R – функция, сопоставляющая вершинам V_R их веса

13. WE – множество весов ребер

14. w_E – функция, сопоставляющая веса рёбрам

Введем унифицированную систему обозначения g-моделей:

где L обозначает множество WV_L, R – множество WV_R, sr – отношение на

w_e – наличие графов-весов ребер g-модели, w_L – наличие графов-весов вершин левой доли g-модели; w_R – наличие графов-весов вершин правой доли g-модели; l – наличие пометок вершин в графах-весах. При отсутствии некоторых параметров, выделенных скобками [ ], получаются различные виды g-моделей. При совпадении в g-модели w_L и w_R будем использовать обычную, то есть не двудольную форму представления g-модели.

Отношение sr определяется типом операции над парой (f_i^lt1, f_j^lt2) и ограничениями на её операнды и результат. В качестве операции выделим операцию определения максимального изоморфного пересечения (МИП), результатом которой является максимальный общий фрагмент (МОФ):

Для помеченных фрагментов МОФ определяется однозначно и результатом может быть Æ. Ограничения на операнды (предикат допустимости P_O(f_i^lt1,f_j^lt2) определяют диапазоны возможного изменения соотношений между f_i^lt1 и f_j^lt2. Ограничения на результат (предикат P_MCF(f_i^lt1Çf_j^lt2, f_i^lt1,f_j^lt2) определяют диапазоны возможного изменения параметров МОФ и возможного изменения соотношений между МОФ и исходными фрагментами:

Определение 1. Матрицей смежности вершин g-модели

называется матрица M_GM(G)=||mсf_ij||; i=1,2,…,k; j=1,2,…,k; для которой mсf ^l_ij - максимальное по числу вершин (рёбер) изоморфное пересечение

Рассмотрим g-модель вида

в которой заменим структурный вес w_e каждого ребра, на расстояние

или

В результате будут построены gs-модели

характеризующие сходство расположения фрагментов f_j^lÎF^l в графе G.

Если учесть орбиты

определяющие симметрию расположения фрагментов типа t в графе G, для t =1,2,…,T, то выделим новый вид g-моделей и gs-моделей, учитывающих число фрагментов в орбите (второй вес вершины (WVN(v)) в g-модели) и характеризующих сходство расположения фрагментов с точностью до орбит групп Aut ^t(G). Обозначим соответственно эти модели как go-модели и gso-модели.

Определим систему стратификации gs-моделей, которая необходима для:

1) обобщения известных отношений подобия, толерантности и эквивалентности графов и выделения новых видов этих отношений;

2) выделения моделей, для которых задачи построения и исследования имеют существенно меньшую вычислительную сложность, чем для gs-модели общего вида;

3) построения на основе gs-моделей иерархической системы структурных и числовых инвариантов с целью систематического исследования их чувствительности при решении задач различения графов (расположения фрагментов в графе);

4) количественного определения значений сложности и сходства графов с учетом расположения фрагментов.

Предлагаемая система включает четыре разреза стратификации:

1) по виду операндов операции Ç и видам иерархии их рассмотрения, ограничениям на вид и результат операции;

2) по признаку выделения отдельных фрагментов gs-модели;

3) по признаку учета или не учета структурных весов вершин и/или ребер gs-модели и видам структурных весов;

4) по частному виду операции Ç (вложение, изоморфизм).

В качестве параметров первого разреза стратификации выделим:

1) вид операции, определяющей отношение sr = Ç, с учетом видов фрагментов структурных весов вершин gs-модели как частей графа (пересечение общего вида – Ç, пересечение вида подграф-подграф – Ç^S);

2) признак связности или несвязности графа, соответствующего весу (w_L^[l]) левой доли или/и весу правой доли (w_R^[l]) gs-модели (^сÇ, Ç^с, ^сÇ^с);

3) высоту окрестности o(f_i^lm) относительно фрагмента f_i^lm(w_L), которая вычисляется от 1 до e, где e – эксцентриситет фрагмента. Результаты пересечения с f_j^ln рассматриваются относительно этой высоты;

4) вид фрагментов, задающих структурные веса (w_L^[l]) левой или/и веса правой доли (w_R^[l]) gs-модели (без циклов – FT, с циклами – F и др.);

5) величину ранга rn(f_i^lm) (веса вершин левой доли gs-модели);

6) разность рангов rn и вид соотношения фрагментов долей gs-модели

7) число компонент связности kс в фрагменте-пересечении mсf^l_ij: kс>1 (любое пересечение); kс=1 (связное пересечение – Ç_с).

Третий параметр приводит к выделению иерархических g-моделей. Это актуально с позиций исследования полноты локальных функций, и имеет как, теоретический, так и прикладной интерес, связанный с построением эффективных алгоритмов структурного анализа систем.

Определение 2. Матрицей смежности вершин иерархической gs-модели H^rw^lF^lw^lÇ(G) окружения r называется матрица M_H(G)=||mсf ^l_ij||; i=1,2,…,k; j=1,2,…,k; для которой mсf ^l_ij - максимальное по числу ребер изоморфное пересечение f_i^lmÇf_j^ln, если (f_i^lmÇf_j^ln)¹ÆÙ(rn(f_i^lm) =ú rn(f_j^ln)-r ç), и 0 (или граф межфрагментного соединения) – в противном случае.

На рис. 1 приведены примеры gso-модели и иерархической gso-модели

которые точно характеризуют сходство расположения орбит подграфов С₃ и С₄ в графе G. В табл. 1 приведены орбиты анализируемых подграфов и расстояния (D1) между орбитами подграфов, определяющие сходство их расположения на основе вычисления максимального общего фрагмента (mcf) для С₃ и С₄ с учетом орбит их расположения в графе. С целью упрощения обозначений в таблице 1 орбиты

обозначим соответственно через Q_i(C_n), Q_ij(C_n,C_m).

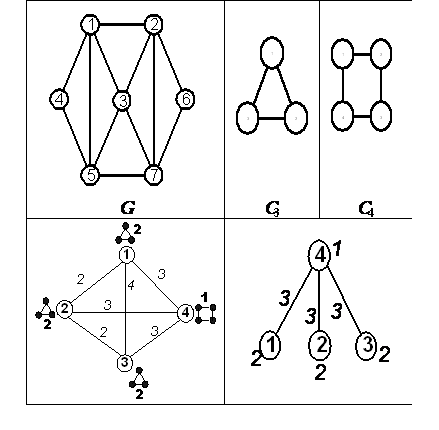
Рис. 1. Граф, анализируемые подграфы и примеры моделей, характеризующих сходство
расположения подграфов и орбит подграфов C3 и C4 в графе G

Пусть заданы две gso-модели [2]:

Таблица 1. Матрицы пересечений орбит подграфов С₃ ,С₄ ,

размеры пересечений и расстояния между орбитами

	Q1(C3)	Q2(C3)	Q3(C3)
Q1(C4)	12, 57	15, 27	15, 27
Число вершин и ребер в пересечении орбит
	Q1(C3)	Q2(C3)	Q3(C3)
Q1(C4)	2, 1	2, 1	2, 1
Орбиты фрагментов, составляющих mcf (С3,С4)
	Q1(C3)	Q2(C3)	Q3(C3)
Q1(C4)	Q11(C3, C4)	Q12(C3, C4)	Q13(C3, C4)
Расстояния между орбитами
D1	Q1(C3)	Q2(C3)	Q3(C3)
Q1(C4)	3	3	3
Орбиты фрагментов, составляющих mcf(С3,С3)
	Q1(C3)	Q2(C3)	Q3(C3)
Q1(C3)	Q11(C3, C3)	Q12(C3, C3)	Q13(C3, C3)
Q2(C3)	Q21(C3, C3)	Q22(C3, C3)	Q23(C3, C3)
Q3(C3)	Q31(C3, C3)	Q32(C3, C3)	Q33(C3, C3)
Расстояния между орбитами
D1	Q1(C3)	Q2(C3)	Q3(C3)
Q1(C3)	0	2	4
Q2(C3)	2	0	2
Q3(C3)	4	2	0

Модели gso₁ и gso₂ изоморфны (gso₁»gso₂), если существуют 1-1 соответствия j: V_1L « V_2L и d: V_1R «V_2R, где i=1,2,…,р_L=úV_1Lç, j=1,2,…,р_R=úV_1Rç и такие что

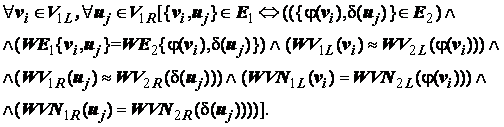
Графы G₁ и G₂ эквивалентны (G₁(gso)G₂) относительно gso-модели

если выполняется условие

Применяя к gso-моделям подход к стратификации g-моделей, получим различные виды gso-моделей, впервые позволяющие определять и исследовать широкий спектр отношений эквивалентности на основе сходства расположения фрагментов графа. Пример системы стратификации gso-моделей, ориентированной на исследование новых видов отношений эквивалентности на основе сходства расположения цепей (P^c), приведен на рис. 2.

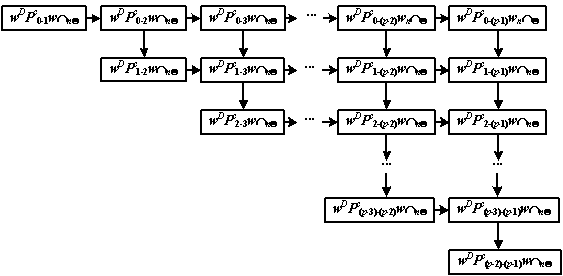
Рис. 2. Система страт gso-моделей для исследования новых видов отношений эквивалентности

Система страт gso-моделей приводит к новым подходам к классификации графов на основе графо-групповых свойств и расширению спектра задач научных исследований. На рис. 3 приведен пример классификация всех транзитивных графов степени 4 на 12 вершинах (рис. 4) с использованием уточняющей классификации системы страт gso-моделей:

Рис. 3. Граф классификации транзитивных графов степени 4 с числом вершин 12

Рис. 4. Диаграммы транзитивных графов степени 4 с числом вершин 12

Предложенные модели программно реализованы в АСНИ «Мастерская граф-моделей» (www.graphmodel.com) [3,4]. Они позволяют студентам и аспирантам ставить и решать новые задачи учебных и научных исследований, среди которых, уточняющая классификация графов и поиск (или обоснования не существования) наименьших по порядку (размеру) графов, gso-модели (подмодели gso-моделей, частичные gso-модели и др.) которых, изоморфны для каждого вида gso-моделей в предложенной системе страт.

ЛИТЕРАТУРА

1. Кохов В.А., Незнанов А.А., Ткаченко С.В. Структурная информатика – новый актуальный раздел информатики для изучения в школе и университете. 1-ое Всероссийское совещание НМС по информатике «Актуальные проблемы информатики в современном российском образовании»: Труды / Отв. ред. Ю.И. Журавлев, В.В. Тихомиров. – М.: МАКС ПРЕСС, 2004. – С. 250-276.

2. Кохов В.А. Граф-модели в структурном спектральном анализе систем. Тезисы докладов МНТК «Информационные средства и технологии», МФИ-2004, Т.1, М, МЭИ, 2004. – С.69-72.

3. Кохов В.А. Решение задач анализа графов и их групп автоморфизмов с помощью ППП «GMW_2.0». М.: Издательство МЭИ, 2002. – 64 с.

4. Кохов В.А., Ткаченко С.В. Решатель базовых задач структурной информатики. М.: Издательство МЭИ, 2006. – 192 с.