BC/NW 2008, №2 (13): 10.3

ОБУЧЕНИЕ БОЛЬШИХ НЕЙРОННЫХ СЕТЕЙ С ПОМОЩЬЮ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ.

Васенко С. М., Кабак И. С.

(г.Москва, ГОУ ВПО МГТУ Станкин, Россия)

В современных системах управления все больше и больше используют элементы искусственного интеллекта. Это могут быть системы управления станками, системы управления летательными аппаратами, ассоциативная память и т.д. Системы с искусственным интеллектом имеют ряд преимуществ над классическими системами, например, повышается точность управления, могут адаптироваться к различным факторам окружающей среды и т.д.

Одним из способов реализации систем с искусственным интеллектом являются нейронные сети. Большие нейронные сети могут решать большое количество разного рода задач. Однако перед использованием эти сети необходимо обучить, перенастроить сеть на решение конкретной целевой задачи. Существуют различные методики обучения НС, но все они очень трудоемки.

В данном докладе предлагается для обучения НС применить метод генетических алгоритмов. Это позволит сократить время и улучшить качество обучения.

Рассмотрим нейронную сеть, построенную по коммутаторной архитектуре (см. рис. 1).

У сети есть входы X1....Xn, выходы Y1...Ym, и промежуточные нейроны. Пронумеруем все нейроны сети числами от1 до N. Обозначим через w_ij вес связи между i–ым и j–ым нейроном. Для удобства примем допущение, что численное значение веса лежит в пределе . Пусть имеется 1 обучающая выборка, в которой имеется K обучающих примеров. Для каждого примера, имея значения на входах нейронной сети, состояние выходов сети заранее известны и считаются «идеальными» для данной задачи. Конечной целью ставится обучить нейронную сеть, то есть сформировать такую матрицу весов W[NxN], чтобы суммарное квадратичное отклонение фактических и идеальных выходов нейронной сети для всех обучающих примеров было минимально.

.

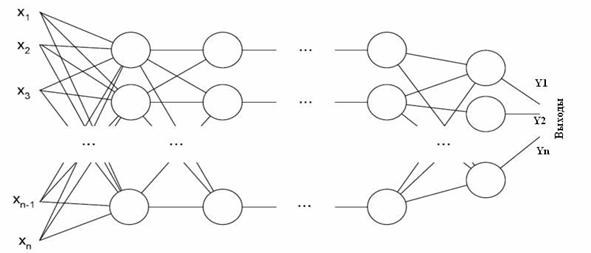
Рис. 1 Общий вид нейронной сети.

Под суммарным квадратичным отклонением будем понимать среднеквадратичное отклонение выходов. Рассмотрим квадратичную сумму для одного примера из выборки:

, (1)

где - значение i – ого выхода нейронной сети при обучающем примере данной выборки, - значение i – ого выхода нейронной сети при реальном результате работы. Следующим шагом необходимо рассчитать квадратичную сумму для каждого из K примеров данной выборки. Для получения конечного результата необходимо составить целевую функцию оптимизации: (2)

Решением будет являться W=min.

Первоначальная матрица весов имеет размерность W[NxN], так как первоначально необученная сеть имеет N нейронов и, возможно, является полносвязной. В процессе обучения сети веса w_ij будут меняться. Рассмотрим один нейронный узел с j-ым нейроном из всей сети (см. рис. 2).

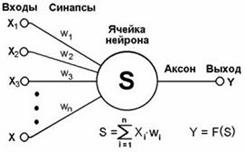
Рис. 2. Общий вид нейронного узла в сети.

Хi – входы j-ого нейрона, Y – выход. Синапсы – группа однонаправленных входных связей, соединенных с выходами других нейронов. Аксон – выходная связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Если функция нейрона (будет приближаться к нулю), то есть и Y=F(S)=0, то это означает, что по аксону данного нейрона не пойдет сигнал возбуждения и выход будет нулевым. Следовательно, входы следующих нейронов, связанных с выходом данного, будут так же иметь нулевые значения. И какое бы значение не принимали соответствующие синапсы, взвешенный сигнал от данного нейрона будет нулевым. А это означает, что данный нейрон оказывает незначительное влияние на конечный результат работы сети, следовательно, результат функционирования сокращенной нейронной сети (не содержащей этого нейрона) будет эквивалентен работе первоначальной сети.

Рассмотрим общую схему обучения нейронных сетей, в соответствие с которой следует вести обучение (см. рис. 3).

Рис. 3 Схема обучения нейронной сети

«Блок ошибки» сравнивает значения выходов сети, полученных после подачи на вход заданных сигналов, и выходов, которые должны получиться при подаче на вход эталонных сигналов. Значение ошибки определяется по формуле . (3)

«Блок обучения» корректирует веса, исходя из среднего квадратичного отклонения ошибки, рассчитанного по формуле (1). Отметим, что для коммутаторной нейронной сети обучение эквивалентно подбору оптимальных коэффициентов матрицы весов W. Задача обучения сведена к задаче оптимизации некоторой целевой функции, имеющей вид (2), а параметрами оптимизации являются элементы матрицы W.

Как уже было отмечено выше, нейроны в разной степени оказывают влияние на общий результат работы нейронной сети. Поэтому одной из функций «Блока обучения » является возможное сокращение сети путем фильтрации (удаления) наименее значимых нейронов. Порядок определения наименее значимых нейронов был рассмотрен ранее.

Изменение размеров нейронной сети в процессе обучения позволит использовать в начале обучения заведомо излишнюю по количеству нейронов сеть, но в процессе обучения ее сократить до достаточного размера для данной задачи.

Отметим, что реализация как программным, так и аппаратным способами меньшей по размеру нейронной сети не только технически проще, но и экономически целесообразнее.

Для того, чтобы приступить к обучению с использованием метода генетических алгоритмов, необходимо сформировать начальную популяцию, то есть какое-то количество матриц весов W^нач. Популяцией называют набор хромосом (решений). Формируются они случайным образом, но с учетом условия . Данная матрица имеет размер [NxN]. В процессе обучения нейроны могут быть удалены из сети вследствие их малого влияния на работу всей сети. Следовательно, размер матрицы весов может уменьшаться. В случае удаления j-ого нейрона из сети, в матрице весов вычеркивается j-ый столбец и j-ая строка. Далее работа будет идти уже с новой матрицей.

Одно из основных понятий в генетике – хромосома. Она однозначно идентифицирует каждую конкретную особь. Хромосома имеет набор генов. Предлагается считать матрицы весовых коэффициентов хромосомами, а элементы этой матрицы – генами данной хромосомы. Для обучения сети к начальной популяции применяются простые операции: селекция, скрещивание, мутация, - в результате чего генерируются новые популяции. После формирования каждой новой популяции управление генетическим алгоритмом передается в блок «ошибки» (см. рис. 3). В данном блоке происходит выявление незначимых нейронов (см. ранее). Если таких нейронов нет, то обучение переходит к следующему шагу. Если такие нейроны обнаружены, то необходимо произвести фильтрацию сети. Алгоритм фильтрации следующий:

1. Запоминается хромосома, которая выявила малозначимый нейрон.

2. Анализируются остальные хромосомы с целью определения степени значимости этого нейрона для других особей. (если его выход нулевой, то нейрон малозначим для сети в целом)

3. Определяется общая значимость нейрона для сети («суммарная значимость»). Суммарная значимость определяется как сумма значимостей данного нейрона для данной особи деленная на количество особей.

4. Если суммарная значимость будет приближаться к нулю, то нейрон можно считать незначимым для всей сети в целом, в противном случае нейрон считается значимым.

Незначимые нейроны можно из сети вместе со всеми связями без потери качества в работе сети. Если после оператора фильтрации нейронная сеть уменьшилась хотя бы на один нейрон, то необходимо составить новую популяцию. Хромосомы данной популяции будут отличаться от хромосом предыдущей ровно на столько генов, сколько нейронов из сети было удалено. Далее генетический алгоритм работает уже с новой популяцией.

У генетического алгоритма есть такое свойство как вероятность. Описываемые операторы не обязательно применяются ко всем хромосомам, что вносит дополнительный элемент неопределенности в процесс поиска решения. В данном случае, неопределенность не подразумевает негативный фактор, а является своеобразной "степенью свободы" работы генетического алгоритма. Оператор селекции (reproduction, selection) осуществляет отбор хромосом в соответствии со значениями их функции приспособленности (коэффициентов выживаемости). Коэффициент выживаемости P_k рассчитывается следующим образом: 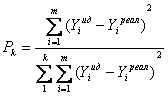, (4)

где k – количество особей начальной популяции, то есть количество изначально сформированных хромосом. Далее для производства потомства необходимо выбрать наиболее приспособленные пары. Выбор происходит по принципу: чем более особь приспособленная, тем больше вероятность того, что эта особь станет родителем. Таким образом формируются пары – «родители». Одна и та же особь, идентифицируемая определенной хромосомой, может стать родителем несколько раз. После селекции слабые особи «погибают», а более сильные выживают.

Следующий важнейший генетический оператор – оператор кроссовера (иногда называют кроссинговер). Кроссовер (скрещивание) – обмен частями хромосом между двумя или более особями. Может быть одноточечный или многоточечный. Для простоты будем использовать скрещивание между двумя особями, и использовать одноточечный кроссовер. Каждая пара родителей с количеством генов N у каждого, могут иметь (N-1) потомков с различным набором генов в хромосоме. У каждой особи из новой популяции так же рассчитывается коэффициент выживаемости и выбираются наиболее приспособленные для дальнейшего произведения потомства. Есть еще один оператор – оператор мутации – стахостическое изменение части хромосом. Он необходим для недопущения попадания популяции в локальный экстремум, а так же способствует защите от преждевременной сходимости. Оператор мутации добавляет в каждую последующую популяцию какое-то число «особей-мутантов». А получается это следующим образом: каждый ген хромосомы, которая подвергается мутации, с малой вероятностью меняется на другой ген. Вследствие этого получается новая особь, которая становится в ряд популяции потомков. Для неё так же считается коэффициент выживаемости.

Обычно при реализации ГА к скрещиваемым особям сначала применяют оператор кроссовера, а потом оператор мутации, хотя возможны варианты. Например, оператор мутации можно применять только если к данной паре родительских особей не был применен оператор кроссовера (свойство вероятности). В принципе, никто не мешает вообще не использовать вероятность проведения данного генетического оператора и применять кроссовер ко всем отобранным особям, а мутацию к каждому 100 потомку. В общем здесь - полная свобода действий.

Таким образом обучение проводится до тех пор, пока суммарное квадратичное отклонение не будет удовлетворять заданным критериям ошибки.

Обучение при помощи генетических алгоритмов проходит в десятки и даже сотни раз быстрее, чем с использованием других существующих способов. Это происходит из-за того, что в генетическом алгоритме решения выбираются по принципу «лучшее оставить, худшее не принимать к дальнейшим расчетам». Например, чтобы обучить полносвязную сеть, состоящую из 4 нейронов на входе, 3 нейронов скрытого слоя и 1 нейрона на выходе, для генетического алгоритма понадобится всего лишь порядка 500 итераций, а для алгоритма обратного распространения – порядка 50000. При этом сеть будет работать с одинаковой предельно-допустимой ошибкой на выходе для обоих случаев.

ЛИТЕРАТУРА

1. В.Дюк, А. Самойленко. Data Mining: учебный курс (+CD). - СПб: Питер, 2001. - 386с. 2. Melanie Mitchell. An Introduction to Genetic Algorithms. Massachusetts Institute of Technology, 1998. - 280.

2. Горбань А. Н. Обучение нейронных сетей // М.:ParaGraph, 1990. 160с.

3. Курейчик В.М. Генетические алгоритмы. Состояние. Проблемы. Перспективы // Известия РАН. ТиСУ. 1999. №1. С. 144-160.