BC/NW 2008, №2 (13): 10.4

Алгебраический анализ технологических связей в автоматизированных производственных системах

Гильфанов Д.Р.,. Коткин Г.Г.

(г. Москва, МГТУ «Станкин», Россия)

При анализе параллелизма технологических операций в автоматизированных системах (см. [1]) применяют алгебраические сети Петри. Важным свойством технологических операций является коммутативность работы системы, отражаемая коммутативной или некоммутативной алгебраической сетью Петри (см. [2]). Классическим примером некоммутативных алгебраических сетей являются сети описывающие установку заявок в очередь на обслуживание. Пусть один из станков устанавливает заявку в одну очередь на доставку заготовки, а в другую – на доставку инструментального комплекта отдельным специализированным робокаром. Тогда может возникнуть «задний» конфликт, если в первой очереди за данной заявкой стоит заявка на доставку загоовки ко второму станку, а заявка на доставку инструментального комплекта ко второму станку стоит ранее заявки первого станка. Вторым способом анализа является анализ конфигурационных пространств методами алгебраической геометрии. Пусть робот обслуживает два станка. Конфигурационное пространство образуется из двух петель условно соответствующих движению руки робота и двух петель, связанных с независимой работой двух станков и топологически эквивалентно фигуре «крендель». Если в эту систему добавить накопитель деталей и заготовок, то появится третья петля и топологическим аналогом данной модели станет шаровидная поверхность с приклеенными двумя «ручками». В общем случае автоматизированная производственная система вклюяает в себя ряд сложным образом взаимосвязанных независимо работающих отдельных подсистем и агрегатов (см. [2]). Одним из важнейших свойств топологичеки эквивалентной модели является род поверхности. Выделяют также особые точки, их кратность и другие характеристики. Приведем оригинальный вывод ряда соответствующих свойств алгебраических кривых.

Предложение 1. Для поля алгебраических функций одной переменной

K(x,y):=C(z,w),

f=åc_skz^Pk+s/dw^k=0, (1)

p_k,dZ₊, положим

w=å_i=0^inf c_iz^Ei (2)

c₀=0 ((0,0)-решение (1)), и определим e₁ из условия p_k+e₁k=p_j+e₁j=

=min_s p_s+e₁s, k!=j (методом диаграммы Ньютона), а c₁ из

_kÎI1 c_skc₁^k=0, I₁:={k:p_k+e₁k=min_s(p_s+e₁s)} (3)

(e₁ определяется неоднозначно, а фиксировав один из таких выборов определяем с₁ как корень (3)); а далее тем же способом e₂ используя подстановку w=c₁z^e1+w₁ и f₁(z,w₁)=f(z,c₁z^E1+w₁). Тогда 1) e₁<e₂<e₃<…, 2) e_i=b_i/d_i=b_i^~/d₀, где d₀=НОК{d_i}<inf, 3) ряд (2) сходится в окрестности z=0.

<<Из _k=0ⁿ _s=0^N c_sk z^Pk+s/d (c₁^k z^S1k+kc₁^k-1c₂z^(k-1)E1+E2+…)=0, после сокращения членов c_0kc₁^kz^Pkz^E1k получаем члены с минимальной степенью c_0kz^Pkkc₁^k-1c₂z^E1(k-1)+E2, а также c_skz^Pk+s/dc₁^kz^E1k, а если члены (sum c_jz^Ej)ⁱ не сократились, то они дают c_0iz^Pic₁ⁱz^E1i. Соответственно этому e₂=e₁+s/d>e_{1 (}уравнение p_k+(k-1)e₁+e₂=ke₁+ p_k+s/d) либо e₂=e₁+d_*>e₁, где d_*=p_i+e₁i-(p_k+ke₁) (уравнение p_k+(k-1)e₁+e₂₌p₁+ke₁+d_*). Пусть теперь e₁,…,e_j определены и сокращаемый член (без коэффициента) имеет вид z ^Ei1 …z ^Eik z ^Pk+s/d. Тогда оставшиеся члены имеют вид 1)z^Ei1…z^Eikz^Pk+l/d или 2) z^Ej1…z^Ejkz^Pk+s/d, l>s, i_l<=j, j_l<=j; или 3) z^Ej1…z^Ej(k-1)z^Ej(k+1)z^Pk+s/d, j_l<=j, в этом случае из минимальности _l=1^ke_jl получаем j_l=i_l, e_jk=max_{l<=k} e_jl или во всяком случае _l=1^k-1e_jl= =_l=1^k-1e_il. Снова получаем e_j+1={e_Ik+(e_Jk-e_Ik); либо e_Ik+e/d_j-s/d_j; либо e_Ik+_l=0^r e_Jl+l/d-(_l=0^k e_Il+s/d)>e_Ik}. Во всех случаях видим e_j+1=>e_i/I<=j; e_j+1=b_j+1/d_j+1, где d_j+1=НОК{d; (d_l),l<=j}, т.е. d₀<inf. Положим теперь

e_*^d0=z, w=_i=1^inf c_i^~e_*ⁱ, (4)

f(e_*ⁿ,w)=f^~(e,w)= c_ks^~ e^sw^k (5)

Тогда по определению w=w₀+ò_e*(w0)^e*(w) (dw/de_*)de_*=

=w₀+ò_e*(w0)^e(w) (-c_sk^~e_*^s-1sw^kde_*)/c_sk^~e^skw^k-1 = _k=0^inf c_k^~ e_*^k, (6)

где c_k^~=d^kw/de_*^k(1/k!). Подстановка (6) в (5) приводит к тождеству, коэффициенты c_i в (2) определены с точностью до выбора корня e_* (4) и при нужном выборе полностью задаются коэффициентами c_k^~. Потому из сходимости (6) вытекает сходимость (2)>>.

Предложение 2. Число точек Вейерштрасса Р (таких, что не существует z_iK(x,y) (z_i)_inf=P^-a[*i], ((a_*1,a_*2,…,a_*p)!=(1,2,…,p)) конечно, а при роде p>1 не равно нулю.

<<Из теоремы Римана-Роха следует W(P^a*i)/W(P^a*i+1)!={0} для пространства дифференциалов W(a_*) делящихся на a_*. Поэтому существуют линейно независимые над K интегралы u_i, (u_ix’dx)=P^a*i-1V_iM^~ - классу дифференциалов поля K(x,y) u_i:=u_ix’dx. Тогда для определителей d_*x=det(u_ix^(k))_{k=1,…,p;i=1,…,p} и d_*t= det(u_it^(k)) имеем

d_*t=d_*x(x_t’)^p(p+1)/2. (1)

Действительно,

u_it^(k)=(u_ix’ x_t’)_t^(k-1)= _s=1^k u_ix^(s)((x_t’)^s)_t^(k-s). (2)

Вычисляя d_*t видим, что для каждого следующего k члены этой суммы с s<k есть линейная комбинация _s=1^k-1 c_s(x,y)u_ix^(s) (для любого i), поэтому линейная комбинация предшествующих строк, и вместо матрицы с элементами (2) можно (выбирая каждый раз независимый вектор) взять матрицу u_ix^(k)(x_t’)^k, d_*=det(u_ix^(k)(x_t’)^k)_k,I= =(x_t’)^(p+1)p/2d_*x. Учитывая, что (d/dt) _k=N^infc_kt^k=_k=N^infc_kkt^k-1, для униформизующей t точки P получаем d_*t=det(t^a*i-kv_ik))_i,k=t^{sum a*i -p(p+1)/2}det(v_ik), где ord_Pv_ik>=0. Установим, что P^{sum a*i -p(p+1)/2} точно делит (d_*t)₀ и поэтому

P^t*i(x_t’^-1)^p(p+1)/2 точно делит (d_*x)₀, для t_*:=t_*i:=sum_s=1^p a_*s-p(p+1)/2 и

d_*x=П_i P_i^t*I (X²/Z_x)^p(p+1) (3)

Для (dx)=Z_x/X², (x)=X₁/X. Достаточно установить, что P^t*+1 точно делит D_t^~=det(t^a*i-k v_ik)_I,k, где v_ik=(a_*i-1)…(a_*i-k+1)u_i^~, при a_*i>=k-1, u_i^~=u_it' t^{k-a*i +1}, так как (d^k/dt^k)(u t^s)=s…(s-k+1)u mod tR для ord_Pu=0, и кольца R точки Р; и

v_ik=(a_*i-1)…1 u_it^{(k-a*i –1)} t^k-a*i, при a_*i <k-1. Вынося множители из строк и столбцов получаем D_t^~=t^t*det(v_ik)_i,k=t^t*det({v_ikпри a_*i>=k-1; 0, при a_*i<k-1})_i,k =:D₁ mod tR. Полагая a_ik:={(a_*i-1)…(a_*i-k+1), при a_*i>=k-1; 0, при a_*i<k-1}, и выбирая из суммы, представляющей каждую следующую строку (a_1k,…,a_pk) независимую подстроку (0,…,0,a_*i^k,…,a_*p^k) получаем

D₁= П_i=1ⁿ u_i^~ det(a_ik)=det(a_*i^~k)_{i=1,…,p;k=0,…,p-1}, где a_*i^~k:={a_i^k, при a_*i>=k-1;

0, при a_*i <k-1}. Так как из (a_*1^~k,…,a_*k-1^~k,a_*k^k,…,a_*p^k)=

=sum_i=0^k-1 c_i(a_*1^~i,…,a_*iⁱ,…,a_*pⁱ) следует (0,…,0,a_*k^k,…,a_*p^k)=

sum_i=1^k-1 c_i(0,…,0,a_*iⁱ,…,a_*pⁱ), и так как det()=

=П_k=1^p a_*k^k-1¹0, то D₁¹0. Теперь из (3) получаем t_*+np(p+1)=deg(D_x)₀=

-deg(D_x))_inf=degZ_x^p(p+1)/2=w_xp(p+1)=(p+n-1)p(p+1)=(p-1)p(p+1)+np(p+1) (где w_x:=2(p+n-1), см. [3]) => sum_i t_*I=(p-1)p(p+1)>0 при p>1. P_i является точкой Вейерштрасса только в случае t_i >0 >>.

Предложение 3. Всякая алгебраическая кривая

f(x,y)=0 (1)

может быть бирационально преобразована в кривую, имеющую только двойные особые точки.

<< Пусть u=sum_s=1ⁿ t_sw_s, u^k=sum_s=1ⁿ t_ksw_s, D=det(t_ks)=D(x,(t_s)),

(x-c)|D, cÎK, (2)

где t_s=t_s(x)ÎK(x), {w_s} – фундаментальный базис K(x,y)/K(x) (любой целый над K(x) zÎK(x,y), z=sum p_s(x)w_s, p_s(x)ÎK[x]), дивизор (x-c)=П_i=1^r p_i^e[i]/X, P_i – точки K(x,y). Покажем, что (2) не возможно.

(d^ju^k/(dv_i)^j)(P_i)=sumc_lj(d^lt_ks/(dv_i)^l)(d^jw_s/(dv_i)^j)=
=sum_s=1ⁿt_ks(x(P_i))(d^jw_s/(dv_i)^j)(P_i), (3)

при j=0,…,e_[i]-1, для униформизующей v_i точки P_i, так как t_ks=t_ks((t_i(x)ÎK(x) => t_ksÎK(x), (d^jt_ks/v_I^j)(P_i)=sum c_r,((m(l))(d^rt_ks/dx^r) П_l (d^m(l)x/dv_i^m(l))(P_i)=0, при

m(l)<=e_[i]-1. Покажем дополнительно, что для любых c_is существует zÎK(x,y) z==sum_s=0^N c_isv_i^s mod v_i^N+1R_i, где R_i – локальное кольцо P_i. Так как существует z^~==c_iv_i^m[i]mod v_i^m[i]+1R_i (для любых c_iÎK, m_iÎZ)/ то элемент z несложно построить по индукции увеличивая степени m_[i] и добавляя соответствующие элементы z^~. Пусть u^k=sum_s=0^infc_iksv_i^s. Тогда (du^k/dv_i)(P_i)=(sum_s=0^inf c_iksv_i^s-(sum_s=0^inf c_iksv_i^~s)|_v[i]~=0)v_i^-1|_v[i]=0. (d^ju^k/dv_i^j)(P_i)=(sum_s=0^infc_ikss(s-1)…(s-j+2)v_i^s-(sum_s=0^inf c_iks s(s-1)…(s-j+2) v_i^~s)|_v[i]~=0) v_i^-1|_v[i]=0=c_ikjj¹sum_l=0^j m_ijlsum_s=0^inf c_iks (lv_i)^sv_i^-j=:sum_l=0^j m_ijlu^k(lv_i)^sv_i^-j |_v[i]=0. Учитывая в столбце только независимый от предшествующих столбцов член суммы и полагая m:= П_i,j m_ijj получаем

det((d^ju^k/dv_i^j)(P_i))_{j=0,…,e[i]-1,i=1,…,…,r;k=0,…,n-1;}=m det(u^k(P_i),

å_s=0^inf c_iks(1.v_i)^sv_i^-1,…,å_s=0^inf c_iks((e_i-1)v_i)^s v_i^-(e[i]-1))_{i=1,…,r;k=0,…,n- 1}|_(v[i])=(0)=

=det()(m/П_i=1^r v_i^r[i])|_(v[i])=(0) =:D₀((v_i ))|_(v[i])=0 ,

где r_ie_i(e_i-1)/2, mÎZ, m!=0. Точка P_ijv соответствует значению униформизующей переменной v_i точки P_i v_i :=jv, P_i0v:=P_i. Как определитель Вандермонда D₀((v_i))|_(v[i])=(0)=(1/П_i v_i^r[i]) П_J1 (u_kv[i],i-u_sv[i],i) П_J2 (u_kv[i],i –u_sv[j],j) П_J3(u_i-u_j)=

=П_J1 (k-s)(du/dv_i)(P_i) П_J2 (u_i-u_j) П_J3 (u_i-u_j)=П_J1 c_i11(k-s) П_i>j (c_i10-c_j10), (4)

u_i:=u(P_i), u_kvi:=u(P_ikv). В силу (3) невырожденная матрица

((d^ju^k/dv_i)^j)(P_i),j=0,…,e_[i]-1,i=1,…,r,k=0,…,n-1) (со столбцами по e_[i] производных для каждой P_i) есть произведение матрицы (t_ks(x(P_i)))=(t_ks(с)) на некоторые векторы ((d^jw_s/dv_i^j)(P_i)), поэтому det(t_ks(с)) !=0, (2) не имеет места. Используя свяь между дискриминантами базисов {u^k} и {w_i} D₁((u^k))=D² D₁((w_i)) и то что

D₁((u^k)):=det Sp(u^kuⁱ)=det(u_i^~k))²_{i=0,…,n-1,k=0,…,n-1} = П_i>j (u_i^~-u_j^~)², (5)

где u_i^~:=g_*iu₀^~:=g_*iu – сопряженные с u корни Irr(u,K(x))=0, g_*iÎG(K(x,y)/K(x)) (см.[3]), покажем, что

D=det(t_ks)=P(x,(t_i))/q((t_i),x)=P^~(x)= П_i P_i(x), (6)

где p_i(x)ÎK((t_i))[x] – неприводимые в K((t_i)) полиномы, не содержат кратных множителей, т.е. P_i(x)¹P_s(x) (любые i¹s). Прежде всего из целости базиса {w_i} и определения t_ks следует, что в представлении (6) qÎK. Для члена в (5) N_{K(x,y,(t[i]))/K(x,(t[i]))} (u_i^~-u_j^~)=N(sum_s (g_*iw_s-g_*jw_s))=

=П_g[*]ÎG sum_s t_s(g_*kg_*iw_s-g_*kg_*jw_s)=П_g[*]ÎG sum_s t_s(g_*w_s-g_*(g_*jg_*i^-1)w_s)= =q_ji(x)ÎK((t_i))[x] – неприводимый полином в силу того, что {w_s} – базис K(x,y,(t_i))/K(x,((t_i)) (значит содержит элемент w_k степени n над K(x,(t_i)), который не может входить в сравнение меньшей n степени).

Если q_ji(x)=c₀q_km(x), где c₀=sum_(k[i]) c_(k[i] П_i t_i^k[I], то u_i^~-u_j^~=c₀(u_k^~-u_m^~);

sum_s t_s(g_*iw_s-g_*jw_s)=sum_(k[i]) c_(k[i]) П_i t_i^k[i] sum_s t_s(g_*kw_s-g_*mw_s), откуда приравнивая коэффициенты при одинаковых П_i t_i^s[i] (t_i транцендентен над K(x,y)) получаем c_(k[i])=0 для всех (k_[i]!=(0,…,0), (g_*i-g_*j)w_s=((g_*k-g_*m)w_s)c₍₀₎ => c₍₀₎=1,

g_*i-g_*j=g_*k-g_*m=g_* (так как {w_s} – базис); {g_*i;g_*j;g_*;g_s, где s не принадлежит {i,j,k,m}}=G(K(x,y,(t_i))/K(x,(t_i)), что противоречит тому, что порядок Группы Галуа (G(..):1)=n=[K(x,y):K(x)]. Поэтому в (6) P_i(x)!=P_s(x) (для всех i!=s). Применяя несколько раз Алгоритм Евклида для полиномов p^~(x)ÎK((t_i))[x] и q^~(x):=d p^~(x)/dx: p^~(x)=q^~(x)h₂(x)+h₃(x); q^~(x)=h₃(x)h₄(x)+h₅(x); …, найдем результант g^~(x,(t_i)): p^~(x)p₀(x)+q^~(x)q₀(x)=g_~(x,((t_i))ÎK[x,(t_i)].

Так как p^~(x) и q^~(x) взаимно просты (p^~(x) не имеет кратных корней в замыкании K((t_i))^a), то g^~(x,(t_i))=g((t_i))ÎK[(t_i)]. Взяв t_i=t_i0ÎK так чтобы g((t_i0))!=0 получаем, что D|_t[i]=t[i0] =D(x,(t_i0)) не имеет кратных корней. Но D=N_K(x,y)/K(x) (D_*) – норма дивизора особых точек (вместо D_* - D в обозначениях предложения 12 (см.(12.1)), т.е. все z такие что D|(z)₀ имеют норму N(z), D|N(z), поэтому D не содержит простых делителей выше, чем в 1-ой степени>>.

Предложение 4. Род p₁ подполя K₁(_K(x,y), [K(x,y):K₁]=r связан с родом p поля K(x,y)

2p-2=r(2p₁-2)+d₀, (1)

где d₀=deg(D), D= П_i,jÎI[0] v_ij^e[ij]-1, I₀:={(I,j): существует c v_ij|(x-c)₀}. (D - дифферента K(x,y)/K₁), e_ij – индекс ветвления точки v_ij K(x,y) над ₁.

<<Пусть v_i – точка K₁, v_ij – точка K₀:=K(x,y) над v_i, e:=e_ij – индекс ветвления, v_i^s | (x-c)_0,K1, - в K₁. Тогда v_ij^{s e[ij]} |(x-c)_0,K0 –в K₀ => v_i^s-1 | (dx)_0,K1, в K₁,

deg_K1 v_i^s-1=(s-1)deg_K1v_i, v_ij^se-1 |(dx)_0,K0, - в K₀,

deg_K0 v_ij^se-1=(s-1)e deg_K0 v_ij +(e-1)deg_K0 v_ij. Если s>1, то v_iÎ|(dx)_0,K1| - принадлежит носителю дивизора нулей дифференциала в K₁, v_ijÎ|(dx)_0,K0| =>

(dx)_0,K0=Con(dx)_0,K1+D, (2)

где конорма Con(П_i v_i^a[*i])=П_i П_v[ij]|v[i] v_ij^{a[*i] e[ij]}. Учитывая, что sum_j e_ij f_ij=r, где f_ij=deg v_ij / deg v_i - степень поля вычетов K₁ над полем вычетов K₀ из (2) получаем (1)>>.

Предложение 5. Среди любой бесконечной последовательности дивизоров a_*1, a_*2,…, a_*1:=(1), a_*k+1=a_*kv_ik^-1, поля алгебраических функций от одной переменной K(x,y) рода p с алгебраически замкнутым K=K^a существует ровно p дивизоров («пробелов») a_*k, для которых отсутствуют элементы zÎK(x,y) с полюсами (z)_inf=a_*k.

<<Не предполагая сначала K=K^a возьмем целый базис w_i,i=1,…,n, K(x,y)/K(y). Тогда элементы

V_r:={w_iy^s,i=1,…,n,s=0,1,…,r} (1)

Линейно независимы над K, поэтому размерность их линейной оболочки

dim Sp_K V_r=nr, а для L(a_*):={zÎK(x,y): (z)>=a_*}

dim V_inf ^ L((y)_inf^N)>= -N d((y)_inf)-s_w, где s_w=max_(i,v)ÎJ ord_v w_i,

J:={(i,v): ord_v (y)_inf <0, i=1,…,n}, d(П_i v_i^a[*i])=sum a_*i d(v_*i), d(v_i) – степень точки v_i. Для дивизоров a_*=П_iÎJy v_i^s[i], J_y:={i: ord_v[i] (y)<0} получаем

d(a_*^-1)-dim L(a_*)<=d(sum_iÎJy v_i)s_w-1 (все y^s в (1) входят в линейно независимые элементы базиса L((y)_inf^N), кроме конечного независящего от N числа, в результате чего dim L((y)_inf^N+1)/L((y)_inf^N)=-d((y)_inf), dim L ((y)_inf^N v_i)/L((y)_inf^N)=d(v_i), при iÎJ_y). Обозначая верхнюю границу через p получаем, что существует a_*0 d(a_*^-1)-dimL(a_*){<=p-1, при a_*>a_*0; =p-1, при a<=a_*0}. Если задана последовательность дивизоров b_*k+1=b_*kv_i[k]^-1<=(1) (для краткости a_*==0 mod b_* обозначаем a_*<=b_*), содержащая r>p пробелов – дивизоров b_*k[s],s=1,…,r, и (z_j)_inf=b_*j (для всех j!=k_s), z_j=p_j(x,y)/q_j(y), то z_jQ(y), где Q(y)=П_j=1^r+1 q_j(y), - целые над K[y] (где x – целый над K[y], p_jÎK[x,y], q_jÎK[x]), g_*s=(Q(y))_infb_*k[s]=П_iÎJy v_i^s[i], поэтому существует (v_s)_inf=g_*s для всех s, кроме не более, чем p значений . Получаем r<=p (таким образом, это следствие теоремы Римана). С другой стороны, если число N точек и число дивизоров b_*k, k=1,…,N, N>2p-2, то из теоремы Римана-Роха –d(a_*)-dim_K L(a_*)=p-1+dim_K W(a_*^-1), где W(a_*^-1) – пространство дифференциалов, аннулирующих распраделения g_*>=a_*^-1 или класс дивизоров M^~/a_* дополнительный к a_* до класса дифференциалов M^~, получаем, что так как deg M^~ =2p-2, то dim_K M^~ /a_*=0 и все r пробелов с необходимостью содержатся в b_*1,…,b_*N >>.

Предложение 6. Пусть задана гиперповерхность

z=f(x₁,…,x_n), (1)

Q_i^k=¶x_i/¶u_k, e_*^k=¶z/¶u_k, f_ij=f_x[i]x[j]’’, f_i=f_x[i]’, N_ik:=C_iQ_k-C_kQ_i,:=sum_i,j f_ijQ_iQ_j, Q_i:=Q_i¹, C_i:=(C)_x[i]’, p_i:=f_i, и выполнены условия интегрируемости уравнений в полных дифференциалах

N₁₂(dp₁+tdp₂+sum_i=3ⁿ Q_idp_i)-C dt=0, (2)

dQ_k/dt=N_1k/N₁₂, (3)

при sum_i,j f_ijQ_i^sQ_j^k=0 (для всех s!=k) (4)

определяющие t:=Q₂,Q₃,…,Q_n, e_*:=e_*¹, при нормированном Q₁==1 (где == - тождественно =), как функции от p₁,…,p_n, где x_i=x_i(u₁,…,u_n),z=z(u₁,…,u_n), u₁,…,u_n – локальные координаты. Тогда (1) – гиперповерхность переноса, т.е. x_i=sum_j=1ⁿf_*ij(u_j), z=sum_j=1ⁿf_*0j(u_j). (5)

<<Для получения (2),(3) продифференцируем (1) по u₁, а затем еще раз по u₁ и по p_s, считая Q_i функциями от t. Обозначая C=sum_i,j f_ijQ_iQ_j, опуская суммы и учитывая, что из

C-(f_iQ_it’-e_*t’) t_u[1]’=0 (6)

следует C/(f_iQ_it’-e_*t’)=t_u[1]’ – функция от t, и 0=(d/dt)(f_iQ_i)=

=¶(f_iQ_i)/¶p_s dp_s/dt + +(¶/¶t)((f_iQ_i-e_*)=sumQ_l (dp_l/dt)+f_iQ_it’-e_*t’ (7)

получаем d(t_u[1]’)/dp_s =(d/dp_s) C/(f_iQ_it’-e_*t’)=(dC/dp_s)(f_iQ_it’-e_*t’)^-1-

-C(d/dp_s)(f_iQ_it’-e_*t’)(f_iQ_it’-e_*t’)^-2=(dC/dp_s) sum Q_l dp_l/dt-

-C ((¶/¶p_s)(f_iQ_it’-e_*t’)) (f_iQ_it’-e_*t’)^-2-C ((¶/¶t)(f_iQ_it’-e_*t’))(dt/dp_s) (f_iQ_it’-e_*t’)^-2 =

=C₀¹ (dt/dp_s)=C₀¹ (¶(f_iQ_it’)/¶p_s)/(f_iQ_it’-e_*t’)= C₀¹ Q_s/(f_iQ_it’-e_*t’); (8)

det((dC/dp_s) sum Q_l dp_l/dt-CQ_st’,Q_s)_s=1,2)=0. (9)

Раскладывая по первому столбцу и снова собирая, получаем

det((dC/dp_s) sum Q_l dp_l/dt)_s=1,2)-Cdet((Q_st’,Q_s)_s=1,2)=0;

N₁₂ sum Q_l dp_l/dt)_s=1,2) - C det=0, (10)

т.е. (2).Если же взять t:=Q_k, то получим (10) с заменой 1-ого определителя на N_1k=det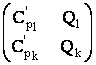. Считая Q_i функциями от t:=Q₂ используем обращение: если x_i=x_i(u₁,…,u_n), то при известных условиях u_i=u_i(x₁,…,x_n). Пусть Q_i=¶x_i/¶u₁ зависит от u₂, тогда можно записать (x_iu[1]’)_u[1]’=(d/du₁)x_iu[1]’(u₁(t,t²),u₂(t,t²))= =(x_iu[1]u[1]”u_1t’+x_iu[1]u[2]”u_2t’)t_u[1]’+(x_iu[1]u[1]”u_1t[2]’+x_iu[1]u[2]”u_2t[2]’)t²_u[1]’=

(t_u[1]’,t²_u[1]’) 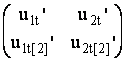((x_iu[1]’)_u[1]’, (x_iu[1]’)_u[2]’)^T=:(t₁^~,t₂^~)U((v₁,v₂)^T (где x_iu[1] означает, т.е. в скобках [] записываем подиндекс). Если t_u[2]’!=0, то t²_u[1]’=x_2u[2]u[1]”=t_u[2]’!=0. Пусть

(x_iu[1]u[1]”u_1t[2]’+x_iu[1]u[2]”u_2t[2]’)=0. (11)

Так как (u_i)-локальные координаты, то det(¶tⁱ/¶u_j)_I,j=1,2!=0=>rkU=2=>(11) возможно только в случае ((x_iu[1]’)_u[1]’, (x_iu[1]’)_u[2]’)((u_j))=

=l_*((u_j)) ((x_iu[1]’)_u[1]’, (x_iu[1]’)_u[2]’)((u_j0)), т.е., если вектор [v₁,v₂]((u_j)) остается пропорциональным себе в некоторой окресности u_j0 (или векторы [v₁,v₂](u₁,u₂,u₃₀,…,u_n0) линейно зависимы при всех u_iÎK – основному полю, i=1,2). Но, если градиент w=(h_u[i]’) некоторой функции h(u₁,u₂) не меняет своего направления в некоторой окрестности B((u_j0)), то он меняет свою абсолютную величину только вдоль w. Получаем, что x_iu[1]’(u₁,u₂,u₃₀,…,u_n0) зависит только от одного параметра, в качестве которого можно взять u₁: x_iu[1]’(u₁,u₂,u₃₀,…,u_n0)= x_iu[1]’(u₁₀,…,u_n0)+I_u[10]^u[1] g(u₁^~)du₁^~ (где I_a^bfdx - интеграл от a до b). Таким образом, (11) имеет место только в случае, когда все Q_i, i=3,…,n, не зависят от u₂, а так как они предполагаются зависимыми от t, то и t не зависит от u₂. В противном случае (11) не имеет места. Проверим, что тогда вместо (3) имеем

¶Q(t,t²)/¶t=N_1k/N₁₂. (12)

Действительно в этом случае

(f_iQ_i)_p[s]’+((f_iQ_i )_t’-e_*t’))(dt/dp_s)+((f_iQ_i )_t[2]’-e_*t[2]’))(dt²/dp_s)=0.

Если последний член для некоторого s не равен 0, то Q_i,i=2,…,n уже не удовлетворяют (2),(3), так как перед dp_s в (2) стоит теперь другой коэффициент. Если же для всех s этот член равен 0, то в подстановке, приводящей к получению матрицы в (9) (f_iQ_i)_Qk’-e_*Qk’=(Q_kp[s]’)^-1(f_iQ_i)_p[s]’ необходимо считать Q_kp[s]’=(d/dp_s)(Q_k(t,t²)|_t[2]=const)=(¶Q_k(t,t²)/¶t)(dt/dp_s), поэтому получаем (12). Если теперь через Q_k обозначить не решение (2), (3), а Q_k:=¶x_k/¶u₁, где x_k, z – удовлетворяют (1), то получаем Q_k(u₁,u₂₀,…,u_n0)= Q_k(u₁₀,…,u_n0)+

+ò_u[10]^u[1] N_1k/N₁₂ t_u[1]’du₁+ò_u[10]^u[1] (¶Q_k(t,t²)/¶t²) t²_u[1]’du₁. Таким образом, имеем x_iu[s]u[k]”=0 => x_i=sum_j=1ⁿ f_*ij(u_j). Так как в силу (4) 0=sum f_ijQ_iQ_j^k+

+sum f_iQ_iu[k]’-e_*u[k]’= sum f_iQ_iu[k]’-e_*u[k]’=-e_*u[k]’, то z=sum_j=1ⁿ f_*0j(u_j). Для наглядности приведем вывод системы (2),(3) в обычных (не лежандровых координатах x_i: (f_iQ_i)_x[s]’+((f_iQ_i )_t’-e_*t’))(dt/dx_s)=0;

(d/dx_s)[C/((f_iQ_i )_t’-e_*t’)]=(¶/¶x_s)[C/((f_iQ_i )_t’-e_*t’)]+[C/((f_iQ_i )_t’-e_*t’)]_t’(¶t/¶x_s) пропорционален (¶t/¶x_s). Дополняем эти векторы до матрицы nxn:

det[(C_x[s]’((f_iQ_i )_t’-e_*t’)-Cf_isQ_it’,f_isQ_i,f_2s,…, f_ns)_s=1,…,n]=0;

det[(C_x[s]’((f_iQ_i )_x[l]’dx_l/dt+Cf_2s, f_1s+f_2st, f_3s,…,f_ns)_s=1,…,n]=0;

det[(C_x[s]’,f_1s+f_2st, f_3s,…,f_ns)_s=1,…,n] (f_iQ_i )_x[l]’dx_l/dt+det(f_ij)C=0;

dt/dQ_k=D₂/D_k, где D_k=det[(C_x[s]’,f_1s+f_ksQ_k,f_2s,…,f_k-1,s, ,f_k+1,s,…,f_ns)_s=1,…,n].>>

Предложение 7. Если в условиях предложения 10 существует хотя бы две системы решений (6.2)-(6.4) определяемые t¹, …,tⁿ; tⁿ⁺¹,…,t²ⁿ, то координаты гиперповерхности (6.1) допускают представление в виде сумм абелевых интегралов поля K(t,Q₃), заданного уравнением

R(t,Q₃)=0, (1)

deg_tR=2n:

x_i=sum_j=1ⁿ ò Q_i^jdt^j/ N((t^j,(Q_l^j),e_*^j); (2)

z=sum_j=1ⁿ ò e_*^jdt^j/ N((t^j,(Q_l^j),e_*^j). (3)

<<Часть условий интегрируемости (10.2) имеет вид

N_p[j]’Q_i-N_p[i]’Q_j=0 (4)

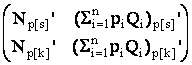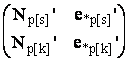Или det=det=0, где N:=N₁₂. Так как e_*=e_*(t), то N=F_N(t). Так как N=(sumf_ijQ_iQ_j)_p[1]’t-(sum c_ijQ_iQ_j)_p[2]’=

=sum c_(k[i],n[j]) Пx_i^k[i] ПQ_j^n[j]t^k[0]=q_N((x_i),(Q_j),t)) – полином, то он не имеет нулей и полюсов (|(q_N((x_i),Q_j0,t₀))₀|=|(q_N((x_i),Q_j0,t₀))_inf|=0) при всех произвольных фиксированных t₀ÎK,Q_j0:=Q_j(t₀) только в случае q_N==0 (тождественно). Заключаем, N=N((Q_i),t)ÎK[(Q_i),t] – полином, не зависящий от x_i (или от p_i:=f_x[i]’(x₁,…,x_n)). Учитывая, что и (6.2) и N dQ_k-N_1kdt=0 содержат полиномы от (p_i),(Q_j),t и дополнив их условиями интегрируемости

F_ij:=(NQ_i)_p[j]’-(NQ_j)_p[i]’=0; F₀:=(NQ_i)_t’-C_p[i]’=0; запишем (10.2) в виде sum g_idp_i+g₀dt=0, где g_i, g₀ – полиномы от Q_j, x_j, t. Далее, следуя основном [3], полагая x_i=sum_j=1ⁿ ò Q_i^j (du₁^j/dt^j)dt^j=sum_j=1ⁿ ò Q_i^jdt^j/N, получаем

z=sum_j=1ⁿ ò e_*^jdt^j/ N>>.

Литература

1. Сосонкин В.Л., Мартинов Г.М. Системы числового программного управления. М.: Логос, 2005.

2. Лескин А.А., Мальцев П.А., Спиридонов А.М. Алгебраические модели гибких производственных систем. -Л.: Наука, 1986. – 150 с.

3. Чеботарев С.Н. Теория алгебраических функций. М.: Едиториал УРСС, 2004.