BC/NW 2008, №2 (13): 11.1

ИССЛЕДОВАНИЕ СПОСОБОВ УСКОРЕНИЯ МЕТОДА ФРАКТАЛЬНОГО СЖАТИЯ ИЗОБРАЖЕНИЙ

Калязин Н.А., Гольцов А.Г.

(Москва, Московский энергетический институт(технический университет), Россия)

Метод фрактального сжатия изображений представляет собой метод сжатия с потерями. Это означает, что в общем случае восстановленное изображение не совпадает с исходным. Метод фрактального сжатия основан на устранении избыточности информации, возникающей в изображениях вследствие их самоподобия. Проще говоря, изображение содержит информацию о себе самом.

Рассматриваемый метод имеет ряд преимуществ, среди которых:

- потенциально высокая степень сжатия,

- малое время распаковки,

- возможность восстанавливать лишь часть изображения,

- возможность восстанавливать изображение произвольного размера,

- широкие возможности в выборе параметров сжатия.

Метод ярко выраженно асимметричный. Это означает, что время сжатия существенно больше времени распаковки. Коэффициент симметричности метода (отношение времени сжатия ко времени распаковки) может достигать 1000-10000 [1]. Таким образом, задача ускорения работы метода фрактального сжатия весьма актуальна.

Рассмотрим принципы, лежащие в основе метода.

Ключевым понятием метода является система итерируемых функций (IFS, Iterated Function System), возможность применения которых к проблеме сжатия изображений впервые была исследована Майклом Барнсли [2].

IFS представляет собой набор трехмерных аффинных преобразований, переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (координата по оси X, координата по оси Y, яркость).

Наиболее наглядно этот процесс продемонстрировал Барнсли в [3]. Им введено понятие фотокопировальной машины (рис. 1), состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран и обладающих следующими свойствами:

- линзы могут проецировать часть изображения произвольной формы в любое другое место нового изображения,

- области, в которые проецируются изображения, не пересекаются,

- линза может менять яркость и уменьшать контрастность,

- линза может зеркально отражать и поворачивать свой фрагмент изображения,

- линза должна масштабировать (причем только уменьшая) свой фрагмент изображения.

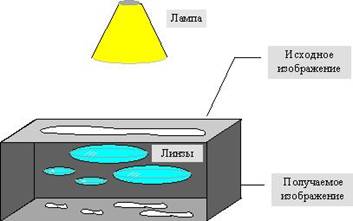
Рис.1. Машина Барнсли

Расставляя линзы и меняя их характеристики, можно управлять получаемым изображением. Одна итерация такой машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций получится изображение, которое перестанет меняться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется «неподвижной точкой» или аттрактором данной IFS. Теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.

Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в изображении. Благодаря самоподобию при любом увеличении наблюдается сложная структура изображения. Таким образом, система итерируемых функций задает фрактал (самоподобный математический объект дробной размерности).

Наиболее известны два изображения, полученных с помощью IFS: «треугольник Серпинского» (рис.2) и «папоротник Барнсли» (рис. 3).

Рис. 2. «Треугольник Серпинского»

Рис.3. «Папоротник Барнсли»

«Папоротник Серпинского» задается тремя, а «папоротник Барнсли» - четырьмя аффинными преобразованиями (или «линзами»). Каждое преобразование кодируется несколькими байтами, в то время как изображение, построенное с его помощью, может занимать и несколько мегабайт.

Фактически, фрактальная компрессия – это поиск самоподобных областей в изображении [4] и определение для них параметров аффинных преобразований.

Рис. 4. Самоподобные области в изображениях

Преобразование , представимое в виде

, (1)

где a, b, c, d, e, f – действительные числа и , называется двумерным аффинным преобразованием.

Преобразование , представимое в виде

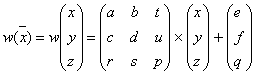, (2)

где a, b, c, d, e, f, q, r, s, t, u – действительные числа и , называется трехмерным аффинным преобразованием.

Пусть - преобразование в пространстве X. Точка , такая что , называется неподвижной точкой (аттрактором преобразования).

Преобразование в метрическом пространстве (X, d) называется сжимающим, если существует число s: , такое, что

. (3)

Теорема о сжимающем преобразовании.

Пусть - сжимающее преобразование в полном метрическом пространстве (X, d). Тогда существует в точности одна неподвижная точка этого преобразования и для любой точки последовательность сходится к .

Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или .

Пусть трехмерное аффинное преобразование записано в виде

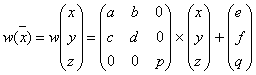(4)

и определено на компактном множестве декартова квадрата . Тогда оно переведет часть поверхности S в область , расположенную со сдвигом (e,f) и поворотом, заданным матрицей

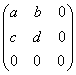. (5)

При этом если интерпретировать значения функции как яркость соответствующих точек, она уменьшится в p раз (преобразование должно быть сжимающим) и измениться на сдвиг q.

Конечная совокупность W сжимающих трехмерных аффинных преобразований , определенных на областях , таких, что и , называется системой итерируемых функций (IFS) [5].

Системе итерируемых функций однозначно ставится в соответствие неподвижная точка – изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии – в проведений итераций системы до стабилизации полученного изображения (неподвижной точки IFS).

В дальнейшем области будут именоваться блоками, а области - доменными [5] (рис. 5).

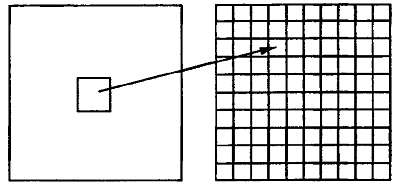
Рис. 5. Перевод доменного блока в ранговый

Проиллюстрируем итерационный процесс восстановления ранее сжатого изображения (рис. 6).

Рис. 6. Исходное изображение

На каждой итерации производится применение IFS к текущему изображению. На рис. 7. показаны изображения, соответствующие каждой из 10-ти первых итераций (включая 0-ю).

Рис. 7. Процесс восстановления изображения

Для оценки качества восстановленного изображения применяется количественная оценка искажений, называемая пиковым соотношением сигнал/шум (PSNR – peak signal-to-noise ratio) [6]. Она рассчитывается по следующим формулам:

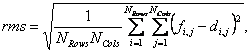(6)

(7)

где и - количества столбов и строк, M – максимальное значение яркости пикселя, - пиксельное значение исходного изображения в i-ой строке и j-м столбце, а - пиксельное значение декодированного изображения, rms – погрешность, вычисленная по методу наименьших квадратов.

Для выявления наиболее узких мест (с точки зрения быстродействия) мною был реализован простейший алгоритм фрактального сжатия.

Опишем более подробно последовательность действий, выполняемых при сжатии изображения.

Исходное изображение разбивается на некоторое количество ранговых блоков. В общем случае ранговые блоки могут быть любой формы и размера, однако должны покрывать все изображение и не должны пересекаться.

Кроме того, исходное изображение разбивается на доменные блоки. В общем случае доменные блоки также могут быть любой формы, могут пересекаться, но обязательно должны быть больше ранговых блоков.

Далее, для каждого из ранговых блоков находится наиболее подобный ему доменный блок. При этом доменный блок может подвергаться аффинным преобразованиям, то есть может поворачиваться на любой угол, зеркально отражаться, у него могут изменяться яркость и контрастность.

В выходной файл для каждого рангового блока записываются координаты соответствующего ему доменного блока, а также коэффициенты аффинных преобразований, которые необходимо произвести над доменным блоком, чтобы он стал максимально подобен этому ранговому блоку.

В таком виде задача не имеет решения, так как для каждого из ранговых блоков необходимо перебрать бесконечное количество разнообразных по размерам и форме доменных блоков. Поэтому на практике накладываются довольно жесткие ограничения, позволяющие сократить количество перебираемых доменных блоков [5]. Разумеется, при этом страдает качество восстановленного изображения. Приведем ограничения, наложенные при реализации алгоритма:

1. Все блоки являются квадратами со сторонами, параллельными сторонам изображения. Таким образом, изображение равномерной сеткой разбивается на набор ранговых блоков (рис. 8а).

2. При переводе доменного блока в ранговый уменьшение размеров производится ровно в 2 раза. Это существенно упрощает как компрессор, так и декомпрессор, так как задача масштабирования небольших блоков является нетривиальной.

3. Доменные блоки берутся «через точку» и по вертикали, и по горизонтали (рис. 8б).

4. При переводе доменного блока в ранговый поворот квадрата возможен только на 0, 90, 180 и 270 градусов. Также допускается зеркальное отражение. Общее число возможных преобразований (считая пустое) – 8.

а

б

Рис. 8. Принцип разбиения изображения на ранговые (а) и доменные блоки (б)

Степень подобия рангового и доменного блоков я вычислял при помощи следующей формулы:

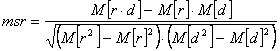, (8)

где r и d – соответственно значения яркостей пикселей рангового и доменного блоков, M – математическое ожидание значений яркостей соответствующего блока.

Эта формула основана на расчете коэффициента корреляции.

При восстановлении исходного изображения была использована формула

, (9)

где r – значение блока восстанавливаемого изображения, d – значение блока преобразовываемого изображения, p – изменение контраста блока, q – сдвиг по яркости блока.

Чтобы найти коэффициент p, я использовал квадратный корень из отношения дисперсий рангового и доменного блоков:

, (10)

где D – дисперсия значений яркости пикселей соответствующего блока; для тех доменных блоков, у которых msr > 0, и формулу

(11)

для тех доменных блоков, у которых msr < 0.

Чтобы найти коэффициент q, я использовал формулу:

. (12)

Очевидно, что для того, чтобы найти для каждого из ранговых блоков наиболее подобный ему доменный блок, необходимо выполнить гигантский объем вычислений.

Предположим, что n x m - размер исходного изображения в пикселях, rsz – сторона рангового блока.

Тогда количество ранговых блоков в изображении будет

, (13)

а доменных (помня, что сторона доменного блока всегда вдвое больше стороны рангового)

. (14)

Таким образом, необходимо произвести rnum x dnum поблочных сопоставлений, что уже для изображения размером 512 x 512 и стороной рангового блока 8 пикселей составляет 251 920 384. Не стоит забывать, что в рассматриваемом нами алгоритме в каждом таком сопоставлении необходимо организовать цикл по всем пикселям блока для расчета математического ожидания и дисперсии. Более того, время, затрачиваемое на сжатие изображения в градациях серого, в простейшем случае утраивается, если речь идет о цветном изображений (так как для представления информации о яркости и цвете пикселя требуется как минимум три составляющих).

Теперь очевидно, почему множество исследований направлено на ускорение метода фрактального сжатия.

Существует два основных направления таких исследований [6]:

- сокращение числа поблочных сопоставлений,

- ускорение сопоставлений путем повышений производительности вычислений.

К первому направлению относятся методы:

- выделение особенностей доменных блоков,

- классификация доменов.

Второе направление подразумевает использование высокопроизводительных систем и параллельных вычислений.

Метод фрактального сжатия, на мой взгляд, легко подвергается распараллеливанию. Это следует из того, что каждый ранговый блок изображения обрабатывается независимо от других. Следовательно, в идеальном случае, можно достичь коэффициента ускорения, близкого к числу ранговых блоков (разумеется, при возможности запустить вычислительных процессов по числу ранговых блоков).

Основываясь на данной предпосылке, я попытался написать параллельную программу на языке Си с использованием библиотеки MPI (Message Passing Interface). Для эксперимента использовался вычислительный кластер МЭИ, имеющий в своем составе 16 узлов, каждый из которых состоит из двух двухъядерных процессоров AMD Opteron x86_64, 2.2 ГГц [7]. Пиковая производительность кластера составляет 281.6 GFlop/s.

Оказалось, что для реализации параллельного алгоритма необходим лишь один вызов функции широковещательной рассылки данных. Это означает, что рассматриваемая задача крайне слабосвязная, а значит, на пересылки данных между процессами тратится минимальное количество времени.

Замер времени производился лишь в той части программы, которая непосредственно реализовывала алгоритм сжатия. То есть операции чтения из файла исходного изображения и записи в файл результатов оказались вне учета времени.

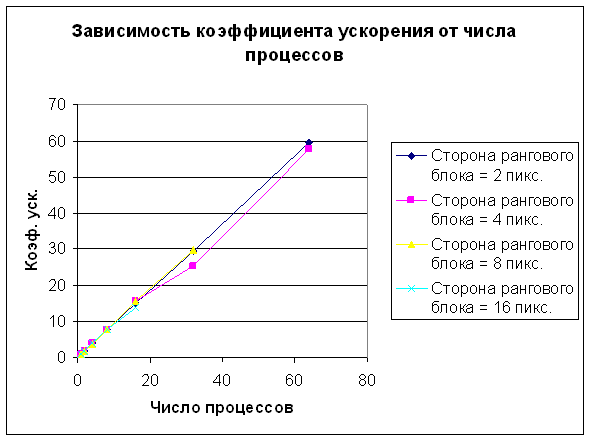
На рис. 9 представлены зависимости времени сжатия изображения от числа параллельных процессов (рис. 9а) и коэффициента ускорения от числа параллельных процессов (рис. 9б) для изображения с разрешением 256 x 256 пикселей. Из диаграммы на рис. 9а следует, что характер зависимости времени сжатия изображения от числа параллельных процессов не меняется при изменении значения стороны рангового блока. Из диаграммы на рис. 9б следует, коэффициент ускорения не зависит от значения стороны рангового блока и численно весьма близок числу параллельных процессов. Последнее наблюдение подтверждает тезис о том, что метод фрактального сжатия хорошо поддается распараллеливанию.

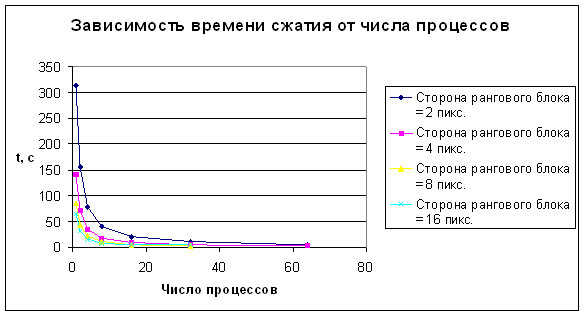
а

б

Рис. 9. Зависимости времени сжатия изображения от числа параллельных процессов (а) и коэффициента ускорения от числа параллельных процессов (б) для изображения с разрешением 256 x 256 пикселей. Линии на каждой из диаграмм соответствуют различным значениям стороны рангового блока

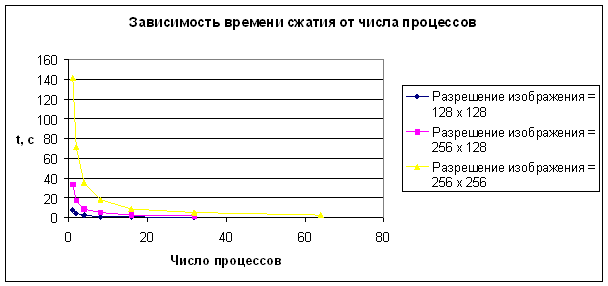
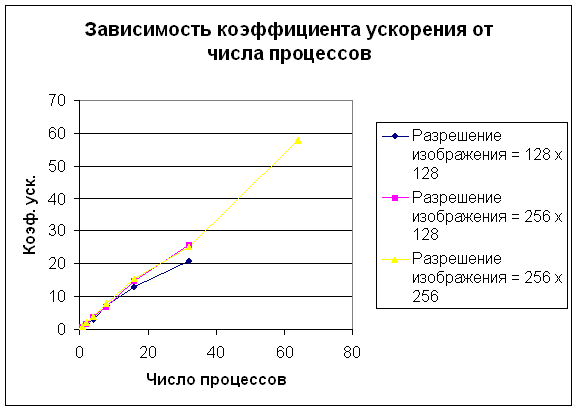
На рис. 10 представлены зависимости времени сжатия изображения от числа параллельных процессов (рис. 10а) и коэффициента ускорения от числа параллельных процессов (рис. 10б) при стороне рангового блока равной 4 пикселя. Из диаграммы на рис. 10а следует, что характер зависимости времени сжатия от числа процессов не меняется при изменении разрешения сжимаемого изображения. Из диаграммы на рис. 10б следует, что коэффициент ускорения не меняется и от разрешения сжимаемого изображения. Это говорит о том, что фрактальный метод сжатия одинаково хорошо распараллеливается для изображений всех размеров.

а

б

Рис. 10. Зависимости времени сжатия изображения от числа параллельных процессов (а) и коэффициента ускорения от числа параллельных процессов (б) при стороне рангового блока равной 4 пикселя. Линии на каждой из диаграмм соответствуют разрешениям исходного изображения

В дальнейшем планируется исследование методов ускорения, основанных на сокращении числа поблочных сопоставлений, а также возможность их распараллеливания. Известно [6], что выделение особенностей доменных блоков и классификация доменов существенно сокращают время сжатия сами по себе – параллельный алгоритм, включающий в себя эти методы ускорения, выглядит еще более перспективным. Однако написание такого параллельного алгоритма может стать довольно сложной задачей.

ЛИТЕРАТУРА

1. Ватолин Д. С. Тенденции развития алгоритмов сжатия статических растровых изображений // Открытые системы сегодня. - 1995. - № 8 (29). – с. 25–30.

2. Barnsley Michael F. Fractal Image Compression, AK Peters, Ltd., 1993.

3. Barnsley Michael F. Fractals Everywhere, second edition, Academic Press, San Diego, 1993.

4. Jacquin A. Image Coding Based on a Fractal Theory of Iterated Contractive Image Transformations // IEEE Transactions on Image Processing. 1992. Vol. 1, N 1. P. 18–30.

5. Ватолин Д., Ратушняк А., Смирнов М., Юкин В. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. – М.: ДИАЛОГ-МИФИ, 2003. – 384 с.

6. Уэльстид С. Фракталы и вейвлеты для сжатия изображений в действии: Учебное пособие. – М.: Издательство Триумф, 2003, - 320 с.

7. Информационно-аналитический центр parallel.ru, “Кластерные установки России и СНГ”, http://parallel.ru/russia/russian_clusters.html.