BC/NW 2008, №2 (13): 12.2

Применение вычислений с исключением ошибок округления для реализации алгоритмов вычислительной геометрии

Орлов Д.А.

(Москва, Московский энергетический институт (ТУ), Российская Федерация)

Алгоритмы вычислительной геометрии используются в различных областях вычислительной техники. Две основные – компьютерная графика реального времени и САПР. Особенностью алгоритмов вычислительной геометрии является их чувствительность как к ошибкам округления при задании входных данных, так и к вычислительным ошибкам внутри самого алгоритма. Причиной этого является то, что из-за вычислительных ошибок могут происходить качественные изменения: выпуклый многоугольник может быть воспринят как невыпуклый, параллельные прямые – как пересекающиеся. Вследствие этого на выходе алгоритма можем получить результаты, серьёзно отличающиеся от истинных. В некоторых случаях возможно даже зацикливание алгоритма [1]. Подобные ситуации назовём вычислительными аномалиями. Тем не менее, в большинстве систем данные представляются числами с плавающей запятой, арифметические операции над которыми, как правило, вычисляются неточно. Следовательно, существует возможность возникновения вычислительных аномалий в процессе работы реализаций алгоритмов вычислительной геометрии для современных ЭВМ.

На сегодняшний день разработаны различные способы снижения влияния ошибок округления на результат алгоритма, однако они зачастую приводят к усложнению алгоритмов и не всегда гарантируют отсутствие вычислительных аномалий. Данная работа посвящена созданию библиотеки, обеспечивающей отсутствие вычислительных аномалий в процессе выполнения алгоритмов вычислительной геометрии. Библиотека использует как алгоритмы контроля ошибок округления, так и алгоритмы вычислений с исключением ошибок округления. Таким образом, программисту нет необходимости выявлять вычислительные аномалии самостоятельно.

Далее приведён пример неверного функционирования программной реализации одного из часто встречающихся алгоритмов вычислительной геометрии, а именно определения взаимного расположения точки и плоскости. Реализация рассматриваемого алгоритма использует 32-битные числа с плавающей запятой (тип float в языках C/C++).

Дана плоскость, пересекающая оси координат в следующих точках: (1009;0;0), (0;1013;0), (0;0;1019). Необходимо определить расположение точки относительно данной плоскости. Решение этой задачи состоит в подстановке координат проверяемой точки в левую часть уравнения плоскости. Если полученный результат >0, то точка лежит над плоскостью (относительно оси z), если <0 – то под плоскостью. Для рассматриваемой плоскости уравнение можно записать как:

(1)

или:

(2)

Проверим расположение точки (227;802;-17). Точное значения выражения (2) для данной точки равно -1, то есть данная точка находится под рассматриваемой плоскостью. Однако, используя числа с плавающей запятой одинарной точности (длина числа 32 бита), и код вычисления выражения, показанный на рис.1, получим результат, равный 6, что означает, что данная точка была ошибочно воспринята как лежащая выше плоскости, то есть, принадлежащая другому полупространству. Более того, используя для вычисления формулы (2) тот же фрагмент исходного кода, получим, что точки (1009;0;0), (0;1013;0), (0;0;1019) не принадлежат данной плоскости, т.к. полученные значения не будут равны 0. Обратите внимание, что максимальные абсолютные величины значений координат характерных точек в этом примере порядка 1000, а значения всех координат – целые.

float resf=-(float)a*(float)b*(float)c;

resf+=(float)b*(float)c*(float)x+(float)a*(float)c*(float)y

+(float)a*(float)b*(float)z;

Рис. 1. Пример исходного кода, определяющего взаимное расположение прямой и плоскости

Отметим, что задача определения взаимного расположения точки и плоскости возникает во многих алгоритмах вычислительной геометрии, неверный её результат может привести к неверному результату всего алгоритма. Поэтому проблема обеспечения точных результатов вычислений и правильности функционирования алгоритмов вычислительной геометрии актуальна.

Для алгоритмов вычислительной геометрии можно ввести понятие топологической целостности данных [2]. Под топологической целостностью понимается сохранение определённых отношений между объектами, являющимися входными данными алгоритма. Например, если в результате ошибок в задании координат вершин выпуклый многоугольник сохранил свойство выпуклости, то топологическая целостность не нарушена. Ошибки округления могут приводить к нарушению топологической целостности данных, что в сою очередь, приводит к вычислительным аномалиям.

Пусть необходимо вычислить y=f(x). Если f(x) – непрерывна, то ошибки округления оказывают незначительное влияние на результат (график слева на рис. 2). Если f(x) – имеет особые точки, то ошибки округления могут привести к результату, не имеющему ничего общего с истинным (график справа на рис. 2).

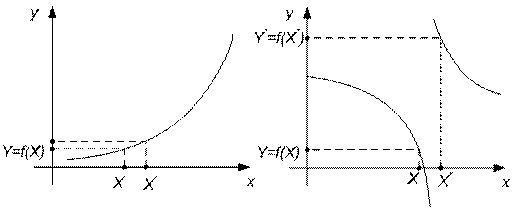
Рис. 2. Влияние ошибок округления в случае непрерывной функции и функции, имеющей разрыв

Проиллюстрируем этот эффект на следующем примере: вычислим выражение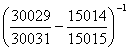. Точное значение этого выражения 450915465. Однако, программа, приведённая на рис. 3, даёт результат ‑18127660.

float d=30031.f/30029.f;

float res=1/(1/d-15014.f/15015.f);

Рис. 3. Пример программы, из-за ошибок округления дающей неверный результат

Подобный разрыв в значениях получается из-за неточного вычисления разности дробей. Точное и приближённое значения знаменателя имеют разные знаки. Это приводит к существенному различию значений их обратных величин, несмотря на то, что абсолютная погрешность вычисления невысока.

Основными подходами, используемыми для обеспечения правильной работы алгоритмов вычислительной геометрии, являются:

1) увеличение разрядной сетки;

2) использование проверки чисел на равенство с заданной точностью;

3) изменение порядка операций над числами;

4) отдельная обработка вырожденных и близких к ним случаев.

Наиболее очевидным подходом является увеличение разрядной сетки чисел с плавающей запятой. В некоторых случаях этот подход может быть эффектным, однако он не устраняет вычислительные ошибки полностью. Оригинальная реализация этого способа, ориентированная на 3D графику реального времени, представлена в [3].

Следующий подход состоит в замене проверок равенства двух чисел с плавающей запятой проверками на их достаточную близость, то есть проверками того, что модуль их разности меньше достаточно малого числа ε. Подобный прием используется при проверке на равенство нулю результата некоторого выражения (например, при проверке нахождения трёх точек на одной прямой). В этом случае необходимо достаточно точно оценить ε, чтобы правильно полученные различные значения не принять за ноль.

В некоторых случаях погрешность вычислений помогает снизить третий подход – внесение изменений в порядок операций над числами. Например, желательно избегать сложений и вычитаний чисел, сильно различающихся по абсолютной величине.

Четвёртый подход состоит в разбиении геометрической задачи на несколько случаев, и использовании для каждого из них своего алгоритма решения. Желательно отдельно рассматривать более простые частные случаи, вырожденные случаи, а также случи, наиболее подверженные влиянию ошибок округления (например, случай пересечения «почти параллельных» прямых) [4].

Большинство перечисленных подходов имеют следующие недостатки: чрезмерное усложнение алгоритма, отсутствие универсальности.

Подход, основанный на применении вычислений с исключением ошибок округления, лишён подобных недостатков.

Под вычислениями с исключением ошибок округления понимается класс алгоритмов представления чисел и выполнения операций над ними, при использовании которых результаты определённых операций над числами могут быть представлены точно.

Использование вычислений с исключением ошибок округления для устранения вычислительных аномалий имеет следующие достоинства: универсальность, отсутствие необходимости модификации алгоритма, возможность полного устранения вычислительных ошибок. Недостатками данного подхода являются: рост требуемого объёма памяти, резкое снижение производительности.

Указанные недостатки можно частично преодолеть, применяя вычисления с исключением ошибок округления только в случаях, где вычислительные ошибки могут качественно изменить результат (например, при нахождении знака числа, близкого к нулю). Избежать снижения производительности удаётся за счёт того, что случаи, требующие применения указанного класса вычислений, будут встречаться редко. Основной способ выявления случаев, требующих применения вычислений с исключением ошибок округления – оценка погрешности полученного результата.

Существуют библиотеки, использующие вычисления с исключением ошибок округления для алгоритмов вычислительной геометрии. Примерами таких библиотек могут служить: LEDA [5], CGAL [6], ESOLID. LEDA поддерживает несколько типов чисел: числа с плавающей запятой произвольной разрядности, целые числа произвольной разрядности, рациональные числа, алгебраические числа. Рациональные числа представлены обыкновенными дробями, алгебраические числа представлены направленными ациклическими графами выражений для этих чисел. ESOLID позволяет выполнять логические операции над геометрическими телами, имеющими в качестве граней поверхности до четвёртого порядка включительно.

Все упомянутые библиотеки рассчитаны в основном на использование в САПР. Однако вычисления с исключением ошибок округления могут применяться и в трёхмерной графике реального времени. Например, в библиотеке трёхмерной визуализации WildMagic4 [7] для некоторых геометрических операций также используются обыкновенные дроби.

Разрабатываемая библиотека делится на две части: вычислительную и геометрическую. Вычислительная часть содержит алгоритмы вычислений с исключением ошибок округления, а также алгоритмы, обеспечивающие отсутствие вычислительных аномалий. В ходе исследования разработан алгоритм, позволяющий при наличии ошибок округления обеспечить достоверность результатов, за счёт определения случаев, требующих применения вычислений с исключением ошибок округления. Выявление подобных случаев осуществляется путём оценки погрешности результата. Для этого разработан алгоритм оценки, а в библиотеку введён класс «число с погрешностью», позволяющий автоматически вычислять погрешность результата. При каждой арифметической операции над подобными числами вычисляется не только результат, но и максимально возможное значение погрешности. Например, если число a имеет погрешность Δa, а число b имеет погрешность Δb, то их сумма или разность будет иметь погрешность Δa+Δb. Кроме того, алгоритм использует особенности проведения операций над числами с плавающей запятой сопроцессором архитектуры x86, а именно флаг получения неточного результата арифметической операции в регистре состояния сопроцессора [8]. Это позволяет избежать завышения оценки погрешности, в случае если аргументы операции известны точно, а её результат может быть представлен в формате с плавающей запятой (в отличие от [5]).

Алгоритм выявления случаев, требующих применения вычислений с исключением ошибок округления, следующий: пусть f(x) – функция, имеющая разрыв в точке X, пусть a – значение переменной с плавающей запятой, Δa – оценка погрешности для a. Тогда, если при вычислении f(x) выполняется условие

|a-X|≤Δa (3),

то появляется возможность возникновения вычислительной аномалии, результат операции объявляется недостоверным, а данный случай требует специальной обработки. Аналогично, если при сравнении двух чисел a и b, имеющих погрешности Δa и Δb соответственно выполняется условие

|a-b|≤|Δa+Δb| (4),

то результат сравнения недостоверен и также требуется специальная обработка. Для функций 1/x и sgn(x) условие (3) вырождается в |a|≤Δa.

На данный момент алгоритмы вычислений с исключением ошибок округления реализованы в рациональных числах, которые позволяют вычислять точно результаты четырёх основных арифметических действий: сложения, вычитания, умножения, деления.

Обработка выявленных случаев, требующих повышенной точности вычислений, состоит в повторении расчётов, но уже с использованием вычислений с исключением ошибок округления. Вычисления можно повторять либо вручную, либо автоматически. Автоматическое повторение вычислений избавит разработчика от необходимости самому контролировать ошибки округления. Для автоматического повторения расчётов необходимо хранить историю вычислений. Это можно реализовать, с помощью хранения для каждого объекта, являющегося результатом какой-либо операции, указателей на объекты и типа операции.

Геометрическая часть разрабатываемой библиотеки представляет собой реализацию различных геометрических объектов. В данной библиотеке в качестве вычислений с исключением ошибок округления используются вычисления в рациональных числах, поэтому на геометрические объекты накладывается следующее ограничение: точки их пересечения должны быть представлены рациональными числами, т.е. библиотека не поддерживает работу с кривыми второго и высших порядков. На данный момент реализован двумерный вариант библиотеки. Текущая версия библиотеки может оперировать следующими объектами: точка, набор точек, прямая, отрезок прямой, ломаная. Библиотека содержит реализации следующих алгоритмов: пересечение двух прямых, пересечение двух отрезков, определение ориентации трёх точек, построение выпуклой оболочки. При разработке библиотеки использованы результаты, полученные в [9].

Исходя из вышесказанного следует, что при использовании контроля ошибок округления возникает два уровня вычислений:

• уровень вычислений с плавающей запятой;

• уровень вычислений с исключением ошибок округления.

Если на предыдущем уровне ответ не получен, управление предаётся на следующий уровень. Однако, многие алгоритмы вычислительной геометрии допускают достаточно универсальные способы ускорения. Результатом некоторых алгоритмов вычислительной геометрии является логическое значение, при этом для значительного подмножества наборов входных данных его можно получить, выполняя более простой алгоритм. Так, алгоритмы вычисления пересечения геометрических объектов позволяют отбрасывать случаи заведомо непересекающихся объектов путём гораздо более простой проверки на пересечение их ограничивающих тел (в качестве таких тел используются параллелепипеды (или прямоугольники для двумерного случая)) с гранями (сторонами) параллельными плоскостям (осям) координат. Поэтому можно говорить о трёхуровневой схеме вычислений:

• упрощённый алгоритм;

• уровень вычислений с плавающей запятой;

• уровень вычислений с исключением ошибок округления.

Схема алгоритма вычислений, использующего выше описанный подход, показана на рис. 4.

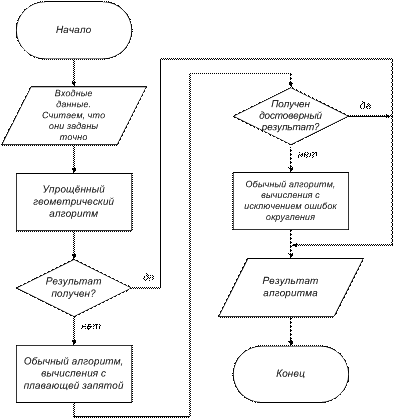
Рис. 4. алгоритм работы с тремя уровнями вычислений

При этом нужно учитывать следующие особенности: для упрощённого алгоритма нет необходимости использовать вычисления с исключением ошибок округления, однако необходимо знать погрешность исходных данных, представленных числами с плавающей запятой. Если погрешность такова, что однозначный вывод о результате алгоритма сделать нельзя, выполняется полный алгоритм, но с вычислениями с плавающей запятой.

В ходе исследования были разработаны и реализованы:

• трёхуровневая схема вычислений с контролем ошибок округления;

• алгоритмы вычислений с исключением ошибок округления;

• алгоритм оценки вычислительных ошибок, вносимых операциями над числами с плавающей запятой

• алгоритм автоматизации процесса обнаружения ошибок и пересчёта результатов.

В дальнейшем планируется произвести экспериментальные оценки производительности разработанных алгоритмов. Также планируется расширить алгоритмы на трёхмерный случай. Кроме того, планируется разработать алгоритм вычислений с исключением ошибок округления, позволяющий работать с иррациональными числами определённого вида, что позволит включить в библиотеку поддержку кривых высшего порядка.

ЛИТЕРАТУРА

1. L. Kettner, K. Mehlhorn, S. Pion, S. Schirra, and C. Yap. Classroom Examples of Robustness Problems in Geometric Computations // ESA, LNCS. 2004. Vol. 3221. P. 702—713. http://www.mpi-inf.mpg.de/~kettner/pub/nonrobust_cgta_06.pdf.

2. Kokichi Sugihara Robust Geometric Computation Based on Topological Consistency

3. Peter Freese Solving Accuracy Problems in Large World Coordinates// «Game Programming Gems 4», Charles River Media, 2004, p.157-170

4. Les A. Piegl Knowledge-guided Computation for Robust CAD // Computer-Aided Design & Applications. 2005.Vol.2. No.5 .p.685-695.

5. Kurt Melhorn, Stefan Näher. LEDA A Platform for Combinatorial and Geometric Computing.

http://www.mpi-inf.mpg.de/%7Emehlhorn/LEDAbook.html

6. CGAL – Computational Geometry Algorithms Library. www.cgal.org

Wild Magic Real-Time 3D Graphics Engine. www.geometrictools.com

7. Зубков С.В. Assembler для DOS, Windows и Unix. – М.: ДМК, 1999. – 640 с., ил.

8. Орлов Д.А. Повышение точности позиционирования движущихся объектов виртуальной реальности // Труды международной научно-технической конференции «Информационные средства и технологии». 16-18 октября 2007 г. В трёх томах Т2. – М.: Полиграфический центр МЭИ (ТУ) С. 199-203