BC/NW 2008, №2 (13): 14.6

ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СИСТЕМЫ ВЗАИМНОЙ ПРОВЕРКИ ЗНАНИЙ

Пудов В.А.

(Москва, Московский энергетический институт (технический университет), Россия)

Методы стандартизованного контроля знаний, при которых тестовая задача сопровождается набором правильных и неверных ответов, во многих случаях оказываются слишком ограниченными, например, когда невозможно задать эталонные решения для данного вопроса. Тогда проверка знаний перекладывается на преподавателя, однако его загрузка в этом случае оказывается очень большой. Компромиссное решение состоит в перенесении части функций преподавателя на самих учащихся путём организации взаимной проверки результатов решения тестовых задач. Применение методов взаимной проверки позволяет не только повысить корректность проверки решений, но и повышает качество подготовки учащихся, их знания и навыки. Система взаимной проверки знаний (СВПЗ) может применяться как в обычной практике обучения (в локальной сети), так и при дистанционном обучении (в глобальной сети).

СВПЗ с подключением арбитра предназначена для контроля уровня подготовленности группы учащихся. Взаимная проверка состоит в оценивании ответа учащегося несколькими его коллегами (самопроверки исключаются) [3]. По результатам оценок выдается заключение о состоянии каждого учащегося (знает, не знает). Для разрешения спорных ситуаций привлекается арбитр (преподаватель), то есть данная система позволяет перенести часть функций преподавателя на самих учащихся, уменьшая его нагрузку. Кроме того, для системы снимаются ограничения на класс тестовых задач (возможно использование открытых вопросов).

Проектирование СВПЗ предполагает организацию связей учащийся-учащийся и арбитр-учащийся и применение такого алгоритма расшифровки результатов проверок, чтобы система могла оценить состояние знаний каждого проверяемого с большой степенью достоверности. При этом учитываются диагностические способности группы учащихся, что снижает загрузку арбитра (преподавателя).

В основе модели системы взаимных проверок лежит принцип распределенного ядра, согласно которому диагностическое ядро системы заранее неизвестно и определяется на основе результатов взаимных проверок: в него включаются учащиеся, правильно ответившие на вопрос и правильно оценившие другие ответы (надежные учащиеся) [1,3].

Система работает следующим образом. Всем учащимся выдается одинаковая тестовая задача, каждый решает ее и передает посредством телекоммуникаций свое решение некоторому множеству абонентов (учащихся) для оценки, состав адресатов может меняться, и заранее неизвестен посылающему [3]. Графически данная система представляется в виде орграфа O = (V,E), где V = {v₁ , v₂ , ... , v_n} – множество учащихся, a E - множество дуг, указывающих на логические взаимосвязи между ними (Рис.1). Оценка a_ij ответов происходит по двухбалльной шкале (зачет-незачет): a_ij = 1, если абонент v_i определяет ответ абонента v_j как неправильный, и a_ij = 0 в противном случае. При этом считается, что если v_i Î G, где G – множество хорошо подготовленных учащихся, то оценка (симптом) a_ij является надежной, в противном случае, v_i Î F (F – множество неподготовленных учащихся), оценка a_ij – ненадежна. В случае, когда v_i Î F, оценка a_ij – произвольна (0 или 1). Такая модель получила название ПМЧ-модели [1]. Совокупность всех симптомов a_ij образует синдром A=< a_ij >. В графовой модели неподготовленные учащиеся интерпретируются как дефектные вершины.

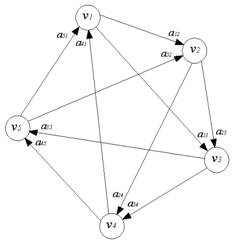
Рис. 1. – Оптимальный граф с n=5

Особенность использования этой модели для проверки знаний состоит в субъективизме взаимных оценок (в отличие от технических систем), что приводит к своеобразным ошибкам, которые получили название враждебных (byzantine) [2] или проблемы византийских генералов. Такие ошибки могут возникнуть в результате следующих причин: 1) механическая ошибка (ошибочное выставление неверной оценки); 2) умышленное выставление неверной оценки; 3) неверная оценка ответа (нехватка знаний проверяющего учащегося для выставления верной оценки) [3]. В дальнейшем, будем называть вершину, которая соответствует учащемуся, неправильно решившему свою тестовую задачу, неисправной (Î F), а вершину, которая соответствует учащемуся, правильно решившему свою тестовую задачу, но неправильно оценившему ответы других учащихся, враждебной (Î BGP, от Byzantine Generals Problem). Совокупность неисправных и враждебных вершин назовём ненадёжными вершинами (учащимися) (Î BS, от Bad Students).

В [3,4] рассмотрены алгоритмы нахождения ненадежных учащихся для полного и оптимального (D_d,t) графов. В случае полного графа имеет место большая нагрузка на каждого учащегося при любом количестве учащихся в группе, так как все вершины графа соединены между собой. В оптимальном графе (Рис.1) число тестовых связей равно nt (где n – количество вершин (учащихся) в системе; t – показатель диагностируемости графа, равный максимальному числу ненадежных вершин, при котором возможна однозначная и правильная расшифровка синдрома A). Определение состояний всех вершин графа (расшифровка синдрома) производится по алгоритму, описанному в [4]. Согласно указанному алгоритму, на первом шаге происходит поиск нулевого контура, содержащего не менее t+1 тестовых связей, или наличие пути с t или более нулевыми дугами подряд. Все вершины нулевого контура и последняя вершина пути, на которую указывает нулевая дуга, входят в ядро. При |BS|>t нулевые контуры также могут существовать (возможно с меньшим числом дуг). В связи с возможным присутствием в системе вершин, принадлежащих множеству BGP, нулевой контур может содержать вершины, принадлежащие не только множеству G, но и множеству BS (F и/или BGP). Следовательно, стоит задача определения вероятности того, что все вершины нулевого контура принадлежат множеству G.

Рассмотрим случай, когда все учащиеся группы имеют примерно одинаковую подготовку по материалу тестовой задачи.

Тогда:

1. Вероятности выставления учащимися, принадлежащими множеству F оценок 0 или 1 одинаковы:

2. Вероятности того, что учащийся v_i принадлежит множеству BGP или F при условии, что учащийся v_i может принадлежать только множеству BS (множеству G принадлежать не может) одинаковы:

Следовательно:

3. Вероятность того, что учащийся v_i, принадлежащий множеству BGP, оценит учащегося v_j, принадлежащего множеству BGP или G, оценкой 0:

4. Вероятность того, что учащийся v_i, принадлежащий множеству BGP, оценит учащегося v_j, принадлежащего множеству F, оценкой 0:

5. Вероятность того, что учащийся v_i, принадлежащий множеству F, оценит учащегося v_j, принадлежащего множеству F, оценкой 0:

6. Вероятность того, что учащийся v_i, принадлежащий множеству F, оценит учащегося v_j, принадлежащего множеству BGP, оценкой 0:

Определим уровень подготовки учащихся как вероятность для любой вершины v_i. Покажем, что при определенном уровне подготовки группы и при наличии нулевого контура в графовой модели, вероятность того, что все вершины контура принадлежат множеству G, становится очень большой и возможно не требуется подключение арбитра.

Пусть нулевой контур содержит m вершин. Рассмотрим следующие события:

– все дуги контура имеют нулевые симптомы.

– не все дуги нулевые.

– все вершины контура принадлежат множеству G.

– все вершины контура принадлежат множеству F.

– все вершины контура принадлежат множеству BGP.

– все вершины контура принадлежат множеству BS (т.е. существуют вершины, принадлежащие множеству и F, и BGP).

– не все вершины принадлежат множеству G или BS (т.е. существуют вершины, принадлежащие множеству и F, и BGP).

– не все вершины принадлежат множеству G или F.

– не все вершины принадлежат множеству G или BGP.

Поскольку пары событий невозможны, то

А

Но

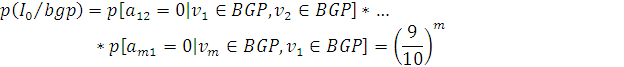
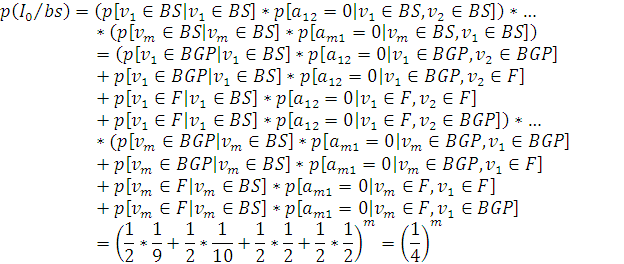
Вероятность того, что все вершины контура принадлежат множеству G:

Вероятность того, что все вершины контура принадлежат множествам F, BGP, BS:

Отсюда,

так как вероятности того, что все вершины контура принадлежат множеству F или BGP, или BS одинаковы. Следовательно,

Тогда:

- вероятность того, что все вершины нулевого контура принадлежат множеству F:

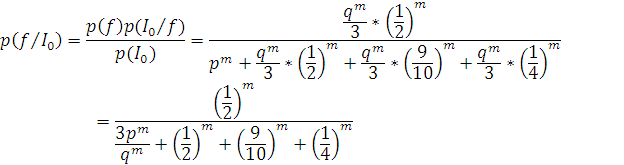
- вероятность того, что все вершины нулевого контура принадлежат множеству BGP:

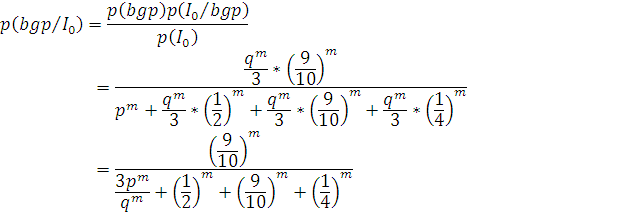
- вероятность того, что все вершины нулевого контура принадлежат множеству BS:

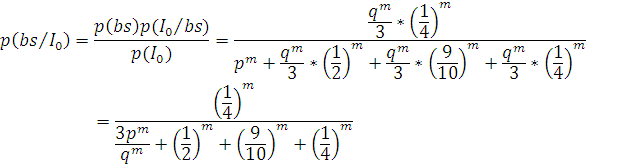
- вероятность того, что все вершины нулевого контура принадлежат множеству G:

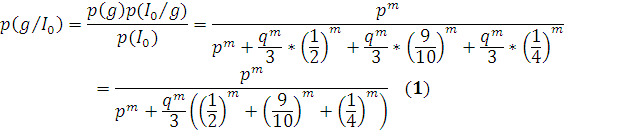
В оптимальной структуре ПМЧ-модели минимальная длина контура m=3. Пусть m=3, p=0,7. Тогда p(f/I₀)=0,003, p(bgp/I₀)=0,019, p(bs/I₀)=0,0004, а p(g/I₀)=0,98, то есть в двух случаях из 100 возможна ошибка в принятии гипотезы о том, что все вершины нулевого контура принадлежат множеству G. При p=0,8 получим p(f/I₀)=0,0006, p(bgp/I₀)=0,004, p(bs/I₀)=0,00008, а p(g/I₀)=0,996. В таком случае подключение арбитра не требуется.

Найдем критическое значение вероятности подготовки группы учащихся p при котором не следует пренебрегать вероятностью возникновения ошибки. В таком случае p(g/I₀) должна равняться 0,95 [5]. Тогда, подставив указанное значение в формулу (1) для m=3, получим:

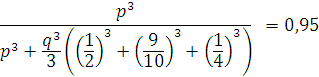
Найдем p:

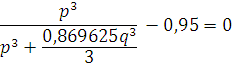
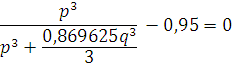
Учитывая, что q=1-p, получим:

Отсюда

Таким образом, при значении вероятности подготовки группы учащихся, равной p=0,64, может потребоваться подключение арбитра или дополнительных тестовых связей [4].

В контуре с числом вершин более трех вероятность p(g/I₀) еще больше. Следовательно, в первую очередь необходимо анализировать контуры максимальной длины. Отметим, что вероятность появления нулевого контура достаточно высока – даже для одного заранее определенного контура из 3 дуг при p=0,7 эта вероятность равна p(I₀)=0,351.

Для сокращения числа взаимных проверок процесс контроля знаний можно организовать, как предложено в [6]. Тогда число тестовых дуг в графе составит (в оптимальной структуре ПМЧ-модели число тестовых дуг nt). Например, для n=7, число дуг составит 14, что на семь меньше, чем в оптимальном графе ПМЧ-модели (Рис.2).

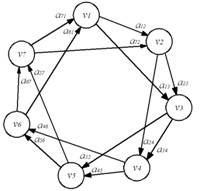
Рис. 2. – Число тестовых связей равно

В заключение отметим, что контрольное подключение арбитра требуется в случае, если группа слабо подготовлена (p<0,7). В этом случае- необходимо подключать арбитра на наиболее информативную вершину, которой является вершина Î F, в которую входит наибольшее количество единичных дуг и которую тестируют обучаемые, признанные надежными [7]. При этом, в случае, когда присутствует учащийся, верно оценивший своих коллег, но которого проверяли только обучаемые, признанные ненадежными, арбитра необходимо подключать именно на этого учащегося в целях выявления его принадлежности к множеству G или F.

ЛИТЕРАТУРА

1. Preparata F.P., Metze G., Chien R.T. On the Connection Assignement Problem of diagnosible systems // IEEE Trans. on Electronic Computers.- 1967, v. EC - 16.- P. 848-854.

2. Lamport L., Shostak R., Pease M. The Byzantine Generals Problem // ACM Transactions on Programming Languages and Systems, Vol. 4, No. 3, July 1982, Pages 382-401.

3. Афонин В.А., Пудов В.А. Проблема византийских генералов при расшифровки синдрома в системе взаимной проверки знаний с арбитром // Международный форум информатизации МФИ-2005. Труды международной научно-технической конференции «Информационные средства и технологии» – М.: Янус-К, 2005. – С. 80-83.

4. Афонин В.А., Пудов В.А. Методика выявления ненадежных учащихся в системе взаимной проверки знаний с арбитром // Международный форум информатизации МФИ-2005. Труды международной научно-технической конференции «Информационные средства и технологии» – М.: Янус-К, 2005. – С. 84-87.

5. Афонин В.А., Смолко А.В. Особенности автоматизации процедуры взаимных проверок знаний на основе модели распределённого ядра // Международный форум информатизации МФИ-96. Тезисы докл. международной конференции “Информационные средства и технологии”, т.3.-М.: Изд-во «Станкин», 1996.-С.67-72.

6. Пудов В.А. Возможные подходы снижения нагрузки учащихся без уменьшения показателя диагностируемости графа в системе взаимной проверки знаний // Международный форум информатизации МФИ-2007. Труды международной научно-технической конференции «Информационные средства и технологии» – М.: МЭИ, 2007, Т.2. – С. 209-213.

7. Пудов В.А., Афонин В.А. Арбитр в системе взаимной проверки знаний // Тезисы докладов четырнадцатой международной научно-технической конференции студентов и аспирантов «Радиоэлектроника, электротехника и энергетика» – М.: МЭИ, 2008, Т.1. – С. 342-343.