BC/NW 2008, №2 (13): 4.3

ИССЛЕДОВАНИЕ МЕТОДОВ РАСПРЕДЕЛЕНИЯ ДАННЫХ ПО ПРОЦЕССОРАМ  КЛАСТЕРНОЙ СИСТЕМЫ ДЛЯ ЗАДАННОГО КЛАССА ПРИКЛАДНЫХ ЗАДАЧ

 

Во Минь Тунг

 

(Москва, Московский энергетический институт(технический университет), Россия)

 

В настоящее время понятие «Многопроцессорные Вычислительные Системы» (МВС), а в частном случае, кластерные системы уже не новшество. В развитии вычислительной техники многое определяется стремлением повысить производительность существующих систем[1]. Мощность первых  компьютеров была очень мала, поэтому решение многих прикладных задач (ПЗ) на них было невозможным или уходило немыслимое количество времени, для их решения. Сразу после появления первых компьютеров, стали придумывать различные методы для объединения нескольких компьютеров в одну единую систему, чтобы повысить производительность и минимизировать время  решения задачи. Идея была проста, если мощности одного компьютера не хватает для решения ПЗ, то надо разделить задачу на две или более части и решать каждую часть на своем компьютере. Это и предопределило появление МВС. В последнее время наибольшее распространение получили кластерные вычислительные системы (КВС).

На практике для решения любой ПЗ на кластерной системе требуется индивидуальный подход, это связано с множественными факторами (спецификой программирования, использования вычислительных ресурсов системы, представлением результатов в нужной форме  и.т.д.), все это требует больших усилий для эффективного использования всей мощности  КВС по сравнению с обычным компьютером. Проблема заключается в том, что на сегодняшний день существует относительно небольшое количество разрозненных методов эффективного распараллеливания задач. Поэтому для реализации ПЗ на КВС специалисту приходится учитывать все особенности  кластерной системы еще на стадии разработки алгоритма ПЗ. Одним из узких мест, в кластерной системе является коммуникационная сеть (КС), от характеристик которой в большей степени зависит время выполнения ПЗ. Наиболее важными характеристиками КВС- являются латентность и скорость передачи данных.[2] Задачи, решаемые на параллельных МВС, можно разбить на классы, определяемые по критерию соотношения времени передачи между процессами и времени выполнения соответствующих процессов. А именно - слабосвязанные задачи, среднесвязанные задачи, сильносвязанные задачи [2].

Большие затраты времени для решения ПЗ происходят за счет передачи данных, это загрузка входных данных в память процессоров, инициализация и межпроцессорные обмены между процессорами. Поэтому для  сокращения времени решения ПЗ, предлагается создать методику  разбиения данных на блоки (массивы) определенной размерности и распределять их по заданным процессорам так, чтобы уменьшить число и  время передач между процессорами.

Для наглядности возьмем, например задачу перемножения матриц, которая используется в очень многих прикладных областях математики, по сути данная задача многим знакома и кажется тривиальной. Например, в задаче «Распределение электромагнитной волны в неоднородной среде, содержащей идеально проводящую плоскость», в модели локально неоднородной среды задача сведена к объемному интегральному уравнению, где на равномерных декартовых сетках с использованием базисных функций специального вида методом Галеркина получена матрица, обладающая трехуровневой блочной структурой [3]. Таким образом, многие задачи, при использовании определенных методов, сводятся к операциям вычисления матриц. При выполнении операций над матрицами небольших размерностей у нас никогда не возникали сложности и проблемы, но если обрабатываются трехуровневые матрицы, матрицы больших размерностей 100000х100000 или 1000000х1000000 элементов будет возникать множество нюансов. Память для хранения матрицы 1000000х1000000 будет составлять 4000 Гбайт и, следовательно, возникает сразу множество вопросов,  как передавать такие данные, как их распределять и.т.д. 

Учитывая характеристики КВС, можно распределять данные так, чтобы можно было бы уменьшить число передач и время передачи. Согласно определению, вычисление элементов результирующей  матрицы при перемножении матриц ||A|| ||B|| имеет вид:

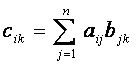 i, k = 1,2,…..n               (1)

где  - это элементы матриц ||A|| и ||B||

         Пусть матрицы ||А||, ||В||, ||С|| квадратные и имеют размерность n*n, для перемножения этих матриц  понадобится время , пропорционально всем  операциям ( где n- сторона матрицы). Для передачи двух этих матриц нам понадобится время t, где  это функция от () операций. При вычислении на кластерных системах,  кроме передач самих матриц будут еще и межпроцессорные обмены, тогда общее время передач станет   ( где t это время на межпроцессорные обмены). Наша задача распределить данные по процессорам таким образом, чтобы сократить общее время решения ПЗ или минимизировать его. 

Рассмотрим более подробно этапы выполнения задачи на КВС:

1) Загрузка данных для управляющего процессора (УП) или иными словами подготовка   задачи и данных.

2) Рассылка данных по процессорам (ПР).

3) Инициализация данных в память процессоров.

4) Обработка.

5) Обмен данными при обработке.

6) Сбор информации в управляющий процессор.

7) Выдача результатов.

Рассмотрим простой метод параллельной организации операций над матрицами на кластере. Построим схему прямого обмена с использованием условных каналов связи на рисунке 1

 

Рисунок 1  Схема прямого обмена.

 

Чтобы не ограничить общность модели конкретной конфигурацией сети, положим, что количество процессоров всегда достаточно для реализации. Построим абстрактную диаграмму работы процессов перемножения матриц, которая представлена на  рисунке 2.

 

Рисунок 2 Временная диаграмма процедур перемножения матриц.

Конечно, это грубое представление, но для нас важно увидеть суть, что при использовании данного метода тратится большое время на многократные передачи матриц по ПР, происходят и многократные загрузки и инициализация данных,  так же возможны межпроцессорные передачи во время  вычисления. При выполнение надо постоянно следить за синхронизацией обменов между УП и ПР, устраивать приоритеты и.т.д. Все это может привести к тому, что мы затратим время на передачи и загрузки намного больше, чем время выполнения задачи. Такой метод хорош, когда скорость передач очень высока и размер данных невелико.

Для устранения перечисленных проблем параллельное выполнение на КВС сделаем с помощью такого метода. Для организации параллельных вычислений, надо разбить матрицы на определенные части для загрузки и распределения по ПР, существует очень много вариантов разбиения, но так как наша система должна быть определена и известна, то матрицы будут разбиты с помощью методов, которые будут приведены ниже.

Рассмотрим КВС гомогенного типа, например кластер SCI, который имеет топологию двухмерный тор [4], Опишем первый метод разбиения матриц. Зная систему, возьмем матрицы для эксперимента квадратные и однородные. Размер подматрицы рассчитывается исходя из количества процессоров. Матрицу результатов ||C|| мы сможем разбить на  (общее количество подматриц в матрице результата ||C||) квадратных частей   ,  где   это сторона подматрицы матрицы ||C|| или количество элементов строки или столбца подматрицы. Коэффициент  будет принимать значение равное числу процессоров  при условии  ( кратно l, l  целое число,   КВС). Исходя, из  выше сказанного на вычислительном узле (ВУ) будет выполняться число операций умножения подматриц . Каждый ВУ кластера SCI в рамках топологии сети (двумерный тор) имеет однонаправленную связь со следующим по горизонтали и по вертикали (последний имеет связь с первым). Таким образом, каждый ВУ присутствует в двух однонаправленных кольцах, или другими словами каждый ВУ кластера SCI имеет связь только с двумя своими соседями по сети. Анализируя кластер, можно увидеть, что минимальное время передач между ВУ обеспечивается только при взаимодействии некоторого исходного процесса с двумя другими при условии, что каждый из процессов расположен на предоставленном только ему процессоре ВУ кластера и ВУ каждого процесса являются соседями по сети (непосредственно соединены). Поэтому для кластера SCI данные будут передаваться строго по осям (x,y) и только для ВУ являющимся непосредственно соседом ВУ, который передает данные. Если учитывать такой обмен, то система распределения заданий (СРЗ) кластера SCI может распределить ряд процессов на процессоры тех ВУ кластера, которые не имеют непосредственной связи с ВУ исходного процесса. Поэтому время обмена между такими процессами больше времени обмена между процессами, расположенными на процессорах ВУ, которые непосредственно соединены с ВУ исходного процесса.

Последовательные стадии  параллельного вычисления для кластера SCI:

1 этап - матрица ||А|| распределяется по горизонтальным полосам вдоль координаты (x,0);

2 этап - матрица В распределяется по вертикальным полосам вдоль координаты (у,0);

3 этап - подблоки матрицы А распределяются в измерении у;

4 этап - подблоки матрицы В распределяются в измерении х;

5 этап - каждый процессор вычисляет одну подматрицу произведения;

6 этап - матрица С собирается из плоскостей (х,у);

 

Рассмотрим кластер ANT, который имеет топологию звезда [4]. Анализируя  (1) можно увидеть, что для получения одной строки матрицы результата мы должны совершить операцию над всей матрицей ||В||. Исходя из этих соображений, матрицу результатов ||C|| мы сможем разбить на l частей, где коэффициент l будет принимать значение равное числу процессоров.  - количество элементов столбца подматрицы ||C||, чтобы получить количество элементов столбца подматрицы ||C||,  (где n кратно k) . Назовем такой метод “однострочного сечения матриц”. Для кластера ANT  будет использован метод однострочного сечения для разбиения матриц, этот выбор сделан из соображения, что в отличие от кластера SCI,  все  ВУ кластера ANT соединены одним коммутатором, другими словами каждый ВУ имеет связь со всеми ВУ кластера. 

Последовательные стадии  параллельного вычисления для кластера ANT:

1 этап - подматрицы А распределяется по ВУ кластера;

2 этап - матрица В распределяется по ВУ кластера;

3 этап - каждый процессор вычисляет одну подматрицу произведения;

4 этап - матрица С собирается подматрицы, собирает их и выводит результат;

Представленные методы не требуют  пересылки данных во время вычисления, осуществляется широковещательная пересылка[5] крупных блоков данных для ВУ. Непроизводительные затраты времени происходят только вовремя загрузки и выгрузки данных, таким образом мы отбрасываем пункт 5 и 6 для данной задачи по сравнению с простым методом, который был приведен в начале.

В данной работе показано, что при определенных методах распределения данных, возможно минимизировать время выполнения ПЗ. Конечно,  в данных методах есть много ограничений, но для нас было важно увидеть, что данное направление изучения является актуальным. Ведь в реальности при решении некоторых задач мы не сможем воспользоваться всеми узлами одновременно, так как некоторые узлы будут заняты для решения других задач. Поэтому в настоящее время ведется анализ различных способов решения поставленной задачи с целью определения наилучшего способа распределения данных в динамике, для минимизации времени решения прикладной задачи. В результате планируется разработать методику распределения и загрузки данных для прикладных задач, руководствуясь которой пользователь смог бы добиться эффективного решения задачи при определенных условиях на конкретной кластерной системе.

ЛИТЕРАТУРА.

1.                 Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ – Петербург, 2002. – 608 с.

2.                 Воеводин В.В. Вычислительная математика и структура алгоритмов. – М.: Изд-во  МГУ, 2006. 112с.

3.                  Савостьянов Д. В., Тыртышников Е. Е.  Применение многоуровневых матриц специального вида, для решения прямых и обратных задач электродинамики.

4.                  Интернет сайт www.parallel.ru

5.                 Немнюгин С.А., Стесик О.Л. Параллельное программирование для         многопроцессорных вычислительных систем. – СПб.: БХВ – Петербург, 2002. – 400 с.