BC/NW 2008, №2 (13): 8.2

сравнительный анализ различных представлений приоритетных очередей.

Зубов В.С., Красков В.В.

(Москва, Московский Энергетический Институт (ТУ), Россия)

Приоритетная очередь (P-очередь), работающая по принципу «элемент с высшим приоритетом обрабатывается (уходит из очереди) первым», используется во множестве приложений. Включение в P-очередь и удаление элементов, изменение приоритета элементов и их положения в P-очереди, – это действия, от вычислительной сложности (ВС) которых зависит время решения задач. P-очередь реализуется на основе древесных структур [1], причем в связанных структурах вычислительная и емкостная сложность больше, чем в бинарной пирамиде – широко используемом варианте P-очереди. В связи с появлением новых пирамидальных структур возникает необходимость сравнения ВС их применений.

Термины, понятия и ряд оценок заимствованы из [1, 2]. Приоритет далее называется ключом элемента. Транспозицией назовем взаимное изменение положения в пирамиде двух элементов. Число элементов пирамиды обозначим N. ëAû означает целую часть A; выражение k₁ .. k₂ – последовательность целых чисел от k₁ до k₂ включительно. Бинарное дерево обозначим БД. При анализе статистических свойств пирамиды полагаем, что значения элементов входного потока распределены равномерно на отрезке [0, 10⁹].

Начнем с уточнения характеристик слабой пирамиды [3], являющейся линейным представлением БД с односторонней упорядоченностью узлов. Каждый узел не меньше всех потомков узла в одной из двух ветвей, называемой правой ветвью этого узла. Не имея левой ветви, корень БД представляет наибольший элемент пирамиды; правая ветвь – это полное БД (рис.1, 2). На рис. 1, 2 в узлах показаны ключи, под узлами – номера узлов. На рис.1 ключи еще не упорядочены. Начала правых ветвей на рис.2 помечены знаком *.

Для построения слабой пирамиды требуется точно (N – 1) сравнение ключей. Это примерно в 1,88 раза меньше среднего числа сравнений, требующихся для построения традиционной пирамиды, которую далее будем называть строгой. Число требуемых обменов элементов не больше N – 1. Найдем среднее число обменов Q.

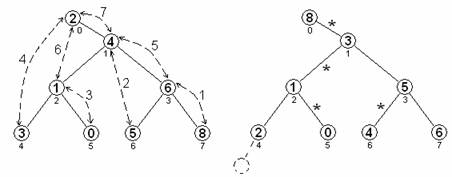
Рис. 1. Исходный набор ключей Рис. 2. Пример слабой пирамиды.

Два ключа статистически эквивалентны (СЭ), если сравнение этих ключей имеет равную вероятность 0,5 его возможных результатов. Ключи полагаются уникальными. Множество (подмножество) статистически эквивалентных ключей назовем статистически однородным (МСО); случайный, не подвергавшийся обработке набор ключей – это МСО. Образуя в нем N/2 пар ключей и проведя в них сравнения, получим два МСО. Ключ, выигравший сравнение (больший из двух), назовем «победителем», другой ключ пары – «побежденным». МСО побежденных ключей присвоим ранг 0. В МСО победителей проведем (попарно) сравнения ключей; вновь получив МСО побежденных ключей, присвоим ему ранг 1. Далее, получая МСО трижды, четырежды победивших ключей и т.д., с помощью серии сравнений выделяем из них очередное МСО побежденных ключей.

Число побед до первого проигрыша определяет ранг ключа, ранг МСО. Процесс завершается получением ключа наивысшего ранга. Такой характер сравнения ключей имеет место при построении слабой пирамиды. На рис.1 номера возле линий со стрелками задают очередность сравнений ключей. В сравнениях участвуют ключи равного ранга или их ранг различается на 1. Вероятность обмена ключей после их сравнения близка к 0,5, поэтому Q » (N – 1)/2, причем Q < (N – 1)/2.

Докажем это. Обмен ключей равного ранга имеет вероятность 0,5. При сравнении ключей разного ранга ключ K₁ большего ранга выигрывает у ключа K₂ с вероятностью p > 0,5. Ключ K₁ всегда ближе к вершине пирамиды, чем ключ K₂ , вероятность обмена этих ключей равна (1 – p) < 0,5. Итак, вероятность обмена после каждого сравнения не больше 0,5. Теперь выясним, сколь часто сравниваются ключи разного ранга.

Назовем неровными поддеревья пирамиды, в которых различна высота левой и правой ветви. Их число V равно числу нулей в двоичном коде числа N –1; ëlog ₂ Nû ³ V ³ 0, N > 1. Число сравнений ключей разного ранга равно V. Если в пирамиду рис.2 включить новый элемент (показан пунктиром), в ней возникнут три неровных поддерева с корнями в узлах 1, 2 и 4. Итак, N = 9, код числа (N – 1) – это 1000, следовательно, V = 3. При N = 9 значение Q меньше (N – 1)/2 примерно на 8%. Если N > 100, Q меньше (N – 1)/2 лишь на доли %.

Для построения строгой пирамиды в среднем требуется » 1,75N перемещений элементов. По опытным данным в большинстве типов компьютеров сложность обмена элементов лишь немного превышает сложность двух перемещений элементов, значение Q примерно соответствует N перемещениям. Следовательно, слабая пирамида выигрывает и по числу транспозиций. Итак, ВС построения слабой пирамиды меньше, чем ВС построения строгой пирамиды. В оценках ВС не учтены вспомогательные действия, характер и объем которых в разных методах различен. Поэтому окончательной оценкой является среднее время построения пирамид, определяемое в эксперименте (рис.3).

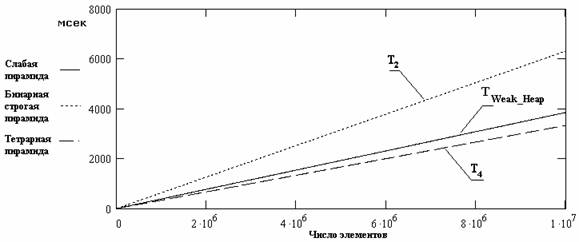
Рис. 3. Среднее время построения приоритетной очереди.

Идея использования слабой пирамиды в P-очереди оригинальна, как и указываемые ниже процедуры. Процедура WeakHeap строит P-очередь из исходного множества элементов. Акт индивидуального включения элемента требует особой процедуры. Логика ее проста: новый элемент включается как лист, будучи помещен в первую свободную позицию массива X, представляющего пирамиду. Возможное нарушение принципа не убывания ключей на трассе, связывающей этот лист и корень пирамиды, устраняется перемещением нового элемента по трассе: выполняются обмены нового элемента с элементами трассы. Включение в слабую пирамиду (см. ниже процедуру InsWeak) логически сложнее, чем в строгую. Включаются элементы массива X с номерами j .. jj. Если j = jj, включается один j-й элемент.

Procedure InsWeak (Var X: Array of tip; j, jj: integer);

Var i, k, t: integer; w: tip; // tip – это тип элемента очереди; key – поле

begin // ключа

If j = 0 then begin r[0]:=0; Inc(j) end;

For j:= j to jj do

begin

r[j]:=0; k:= j div 2; i:= j;

If k+k < j then

If X[k].key < X[j].key then // Первое сравнение включаемого элемента

begin w:=X[k]; X[k]:= X[j]; X[j]:= w; i:=k end

else Continue;

While k > 0 do // Подъем по трассе вставки и упорядочение элемента по

begin // отношению к узлам, в правой ветви которых оказывается X[i]

Repeat t:= k; k:= t div 2 Until (t + r[k]) mod 2 = 1;

If X[k].key >= X[i].key then Break;

w:=X[k]; X[k]:= X[i]; X[i]:= w; r[i]:= 1– r[i]; i:= k

end

end

end;

Процедура InsWeak требует пояснений. Отцом некоторого узла t является узел t div 2, где div обозначает операцию деления нацело. У каждого узла k, не являющегося корнем БД, два сына с номерами 2k и 2k + 1. Какой из них является началом правой ветви, указывается признаком r_k. Если r_k = 0, правым является сын 2k + 1, а если r_k = 1, то сын 2k. Обозначив t номер сына, проверяем значение t + r_k., которое нечетно, если сын – правый. Эта проверка выполняется в цикле, подчеркнутом в тексте InsWeak. В слабой пирамиде, по определению, важна лишь упорядоченность включаемого элемента X[i] с элементами X[k] – «предками слева». В цикле While поиск этих элементов X[k] выполняется до тех пор, пока возможная неупорядоченность X[i] по отношению к этим предкам не будет изжита.

Из исходных N элементов можно построить и всю пирамиду «от нуля», если записать обращение InsWeak (X, 0, N), однако процедура WeakHeap строит ее быстрее.

В слабой пирамиде потенциальное число сравнений включаемого элемента определяется числом «1» в двоичном номере элемента, а ранг элементов, с которыми он сравнивается, – положением этих «1». Фактическое число сравнений, как правило, меньше. Среднее числа C сравнений для одного элемента может быть найдено по номеру элемента с использованием полученных нами вероятностей p_j проигрыша случайного ключа ключам ранга j = 0, 1, 2, … и т.д. (табл. 1).

C = 1 + å p_j, где 1 соответствует обязательному первому сравнению, суммируются p_j для рангов j < ëlog₂ nû тех предков X[k] включаемого элемента X[i], в правой ветви которых находится X[i]. Усредняя C на множестве N включаемых элементов, получаем удельное число C_уд, стремящееся к 1,832 с увеличением числа N.

Удельное число C_уд, получаемое в статистическом эксперименте с применением InsWeak, равно 1,78. Оно отличается от 1,832 менее, чем на 3 %. Несовпадение вызвано упрощенной моделью. Для строгой пирамиды

Ранг	0	1	2	3	4	5	6
p	0.6667	0.4667	0.2890	0.1630	0.0874	0.0452	0.023

Табл. 1. Вероятность проигрыша случайному элементу.

экспериментально получено C_уд = 2,28.

Среднее удельное число обменов элементов Q_уд примерно на 1 меньше C_уд: как правило, перемещение элемента по трассе заканчивается сравнением с внутренним элементом пирамиды (без обмена). Даже если трасса доходит до корня пирамиды, обмен нового и корневого элементов происходит редко. Так, согласно табл.1, при включении элементов с номерами, превосходящими 128, вероятность такого обмена меньше 0,0116.

Итак, характеристики ВС акта включения элемента в слабую пирамиду, в том числе среднее время включения, лучше аналогичных характеристик для строгой пирамиды.

Использование P-очереди предполагает процедуру ее восстановления после взятия головного элемента с продвижением следующего по величине элемента в голову P-очереди. Он находится на M-трассе, проходящей через элементы-максимумы в подмножествах узлов, образующих все множество. M-трасса начинается в узле 1, лежит в его левой ветви и от каждого узла проходит в направлении левой ветви. Первый этап – это выявление M-трассы, второй – поиск максимума на M-трассе и продвижение его в голову очереди по способу «пузырька». Чтобы не возник пустой узел, движение от конца M-трассы начинает элемент из последнего листа БД (его номер j задается). По номеру k конечного узла M-трассы номера прочих ее узлов (предков узла k) вычисляются оператором k:= k div 2.

Procedure RestWeak (Var X: Array of tip; Var j: integer); // Восстановление Var k: integer; w: tip;

begin

X[0]:= X[j]; k:=1;

While k+k+r[k] < j do k:=k+k+r[k]; // k - конец M-трассы

While k > 0 do //Этап продвижения по M-трассе и коррекции узлов на ней

begin If X[k].key > X[0].key then

begin w:=X[k]; X[k]:= X[0]; X[0]:= w; r[k]:= 1– r[k] end;

k:=k div 2

end; // Восстановление завершено; X[0] - максимальный элемент

Dec(j) // Уменьшение номера последнего элемента

end;

Если к моменту восстановления очереди известен очередной включаемый элемент Z, применяется процедура RestMWeak, полученная удалением из RestWeak двух операторов: X[0]:= X[j]; Dec(j). До обращения к RestMWeak следует выполнить оператор X[0]:= Z.

В процедуре RestStrict восстановления строгой пирамиды нет этапа предварительного прохождения трассы, но выполняется примерно в 1,87 раза больше сравнений, поэтому при большой ВС сравнения ключей быстрее работает RestWeak, а при малой – RestStrict.

В целом применение слабой пирамиды в очереди характеризуется меньшей ВС, чем применение строгой бинарной пирамиды. Степень t узлов строгой пирамиды может быть больше двух, например 3 (тернарная пирамида) или 4 (тетрарная пирамида). В общем случае строгую пирамиду называют t-арной. Тетрарная пирамида удобна для исследования. Число выполняемых в ней сравнений почти такое же, как в бинарной, а число перемещений элементов примерно вдвое меньше (как и высота пирамиды). Поэтому с увеличением размера элементов время T₄ построения тетрарной пирамиды стремится к T₂/2, где T₂ – время построения бинарной. Время T₄ заметно меньше времени построения слабой пирамиды (рис.3).

Доля узлов-листьев в t-арной пирамиде приблизительно равна (t-1)/ t, с ростом t эта доля увеличивается, растет и ранг узлов-предшественников листьев. В результате увеличивается вероятность p проигрыша включаемого элемента предшественнику листа. Если в бинарной пирамиде p » 0,578, то в тетрарной p » 0,783. Прямое следствие этого – сокращение трассы включения элемента, числа сравнений и перемещений элементов (в среднем). Для тетрарной пирамиды C_уд » 1,544, удельное число перемещений » 1,336. Налицо заметно меньшая ВС включения в тетрарную пирамиду в сравнении со слабой и строгой бинарными пирамидами.

Осталось оценить ВС восстановления тетрарной пирамиды. Относительно малое число перемещений элементов и вспомогательных действий – основа преимущества тетрарной пирамиды, всегда выигрывающей у строгой бинарной пирамиды.

Если ВС сравнения ключей невелика, что обычно имеет место, время восстановления тетрарной пирамиды примерно в 1,5 раза меньше времени восстановления слабой пирамиды. При 10-кратном увеличении ВС сравнения ключей эти времена выравниваются, так как в тетрарной пирамиде выполняется примерно в 1,87 раза больше сравнений, однако усложняя программу, этот коэффициент можно снизить до 1,4, закрепив тем самым преимущество тетрарной пирамиды.

От традиционного использования в P-очереди бинарной строгой пирамиды следует отказаться. Результаты проведенного анализа ВС операций с P-очередью свидетельствуют о явном преимуществе двух новых пирамидальных ее реализаций. Выбор одной из них для приложения зависит от входных параметров: средних размеров очереди и элемента очереди, сложности сравнения ключей, повторяемости ключей и т.д. Этот выбор предполагает экспериментальную оценку затрачиваемого времени компьютера в характерных случаях применения P-очереди. Она нужна и потому, что приведенные нами оценки актов включения в очередь и ее восстановления абсолютом не являются: при длительной работе очереди ее статистические характеристики изменяются.

Исходные характеристики для всех вариантов используемых пирамид могут быть получены на основе общего анализа, основные результаты которого приводятся ниже.

Пусть k(s) – количество элементов, значения которых по определению соответствующей пирамиды должны не превосходить значение рассматриваемого элемента на s-ом ярусе. (Например, для слабой пирамиды k(s)=2^s-1). Тогда, из свойства упорядоченности пирамиды ясно, что среднее, по всем выборкам значений из [1,n] элементов входного набора, значение элемента на s-м ярусе может быть оценено как

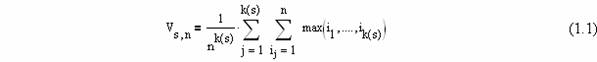Вычисляя данную величину, получаем следующий результат.

Теорема 1. Среднее значение элемента приоритетной очереди, на основе пирамиды (слабой или t-арной) построенной из входной выборки элементов с равномерно распределенными на [1,n] значениями, находящегося на s-м ярусе пирамиды имеет вид

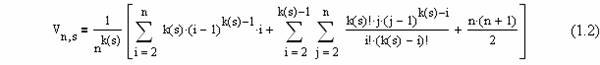
Поскольку имеет место

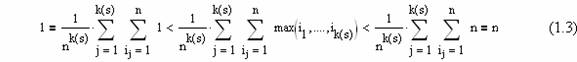обозначим через

вероятность того, что значение случайной величины, равномерно распределенной на отрезке [1,n], попало в интервал [V_j,n ,V_j+1,n]. Здесь K(x) - обратная к k(s) функция.

Следствие 1. Среднее число операций обмена и сравнения, при вставке элемента с равномерно распределенным на [1,n] значением в приоритетную очередь с N элементами на базе слабой пирамиды, есть 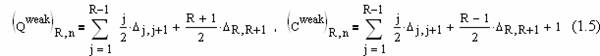соответственно. Здесь R=K(N)=log₂ N + 1 – число ярусов в рассматриваемой пирамиде.

Следствие 2. Среднее число операций обмена и сравнения, при вставке элемента с равномерно распределенным на [1,n] значением в приоритетную очередь с N элементами на базе t-арной пирамиды, имеет соответственно вид

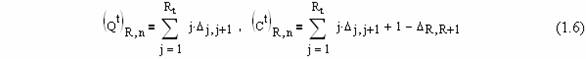Здесь R_t =K_t(N)=log_t((t-1)N + 1).

На рис.4 реализации P-очереди систематизированы по типу используемой структуры данных. Известно, что связанные реализации, в данной статье не рассматриваемые, проигрывают пирамидальным по емкостной и временной сложности. Лесная реализация предполагает использование леса пирамид [4] с целью уменьшения высоты пирамид, ведущего и к уменьшению длины трасс. Это снижает ВС восстановления P-очереди.

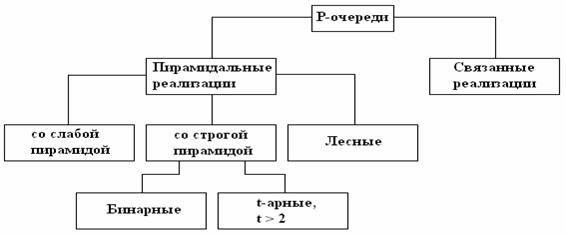
Рис. 4. Варианты реализации приоритетной очереди.

Исследование P-очереди выполнено на кафедре математического моделирования МЭИ с использованием специально разработанных программ, написанных в двух вариантах: на языках Object Pascal и C++. Реализации на двух языках показали достаточно близкие результаты

ЛИТЕРАТУРА

1. Кнут Д.Э. Искусство программирования, том 1. Основные алгоритмы, 3-е изд.: Пер. с англ. М.: Изд. дом «Вильямс», 2001. – 712 с.: ил.

2. Кнут Д.Э. Искусство программирования, том 3. Сортировка и поиск, 2-е изд.: Пер. с англ. М.: Изд. дом «Вильямс», 2000. – 822 с.: ил.

3. Dutton R.D. Weak-heap Sort. – BIT, 1993, Vol. 33. – P. 372-381.

4. Зубов В.С. Справочник программиста. Базовые методы решения графовых задач и сортировки. – М.: Информационно-издательский дом «Филинъ», 1999. – 245 с.