BC/NW 2008, №2 (13): 9.1

Влияние временных задержек на производительность мультисервисных коммуникационных сетей

Широков В.Л., к.т.н.

компания «Ланит»

Аннотация

Предметом данной статьи является исследование связи временных параметров трафика на производительность мультисервисных коммуникационных сетей. Производительность определяется как продуктивность сети, которой соответствует количество одновременно обслуживаемых активных пользователей в течение заданного временного периода. Каждый пакет рассматривается как запрос, поэтому время обработки и передачи пропорционально длинам пакетов. Целью является представление уравнений для расчета производительности мультисервисных коммуникационных сетей в зависимости от длины пакетов, временных периодов, лимитированной задержки, интенсивности обработки и передачи информации.

Введение

В связи с постоянным увеличением объема мультисервисной информации (данные, голос, видео), передаваемой в пакетных сетях, все больше возрастают требования к качеству обслуживания (КО, или Quality of Service – QoS) трафика, генерируемого абонентами-пользователями, системами, подключенными к сети, самой сетью.

Обслуживание мультисервисного трафика заключается в обработке очередей и передаче пакетов между узлами пакетной сети. Каждый пакет передается отдельно от других и может интерпретироваться как индивидуальный запрос [1].

Поскольку сеть состоит из множества узлов и каналов, она моделируется как сеть очередей [2, 4]. Основным параметром КО (QoS) в пакетной сети является средняя скорость передачи. Процессы обработки очередей и передачи пакетов-запросов накладывают определенные ограничения и на время обслуживания (прохождения пакетов по сети) [1, 3].

Структура сети, интенсивность нагрузки и обработки трафика узлами, разбиение пакетов-запросов на кадры-слоты, скорость передачи информации по каналам являются техническими характеристиками сети с коммутацией пакетов. Эти характеристики принимают вполне определенные значения из некоторых фиксированных наборов.

Необходим общий метод, который, используя технические характеристики сети (интенсивность обработки и скорость передачи), параметры нагрузки (число абонентов, их активность, характеристики внешнего трафика), позволяет рассчитать основные параметры КО (фактические скорости и временные задержки пакетов). С использованием полученных значений должны находиться параметры производительности, определяющие фактическое число активных абонентов (пользователей), которые могут быть обслужены, и объем услуг, который может быть выполнен системой. При этом должны определяться также такие параметры сети, как число каналов системы, а для радиосети – также частотный ресурс, число сот, схема размещения базовых станций (БС), конфигурация антенно-фидерных трактов (АФТ).

Ниже предлагается и описывается метод задержек [1, 4], который обеспечивает расчет, оценку и выбор параметров, определяющих производительность мультисервисной сети с коммутацией пакетов.

1. Постановка задачи

Обслуживание пакетов в каждом узле коммуникационной сети (как мультисервисной системы обмена информацией – МСОИ) заключается в обработке и передаче пакетов по соответствующие каналы. При этом определяется фактическая интенсивность обработки и передачи, а по ним время обслуживания в узлах и время передачи в каналах, которые пропорциональны длине пакетов. Поэтому реальной характеристикой, определяющей фактическую скорость обслуживания и параметры производительности МСОИ являются временные задержки (обработки и передачи) [1, 4].

Определения.

Качество обслуживания (КО) – это лимитированная скорость обработки пакетов при передаче трафика между узлами по каналам в фазах контуров сети.

Абоненты сети – это отправители (источники) и получатели (приемники) пакетов.

Нагрузка – это параметры трафика, а именно: активность абонентов и интенсивность пакетов в единицу времени. Нагрузка также подразделяется на внешнюю и внутреннюю.

Внешняя нагрузка – это интенсивность внешнего трафика сети в пакетах в единицу времени и активность источников (абонентов).

Внутренняя нагрузка – это интенсивность внутреннего трафика в пакетах в единицу времени.

Оверхед – это дополнительная информация о пакете в сети (заголовок, концевик, служебная информация, защитный интервал).

Дифференцированные услуги [2] были предложены для обеспечения КО в пакетных сетях (Интернет, интранет, экстранет, VPN, другие сети, использующие IP-протокол).

Эта концепция предусматривает, что в каждом пакете содержатся коды дифференцированных услуг, что позволяет специфицировать трафик в фазах и контурах.

С позиций КО каждый пакет можно охарактеризовать следующими исходными и расчетными параметрами:

· вид услуги U={d, t, v} (фазы φ, контуры Qє{q_d, q_t, q_v}, исходная скорость V₀, период следования t₀, длины пакетов B, активность услуг A);

· лимитированная задержка T_U услуги в контуре в зависимости от вида услуги U;

· интенсивность поступления пакетов γ в сеть;

· фактическая интенсивность пакетов λ в фазах φ контура q;

· интенсивность обработки пакетов в узле μ;

· интенсивность передачи пакетов в канале C.

Для анализа сети очередей используется теорема Джексона (Jackson), которая основана на трех допущениях:

· сеть очередей состоит из {m} активных узлов, соединенных между собой множеством {K} пассивных каналов;

· запросы поступают в систему снаружи на любой из узлов с частотой, распределенной по Пуассону;

· каждый из узлов предоставляет независимое обслуживание с экспоненциально распределенным временем;

· после обслуживания в узле запрос немедленно, с некоторой фиксированной вероятностью, поступает через пассивный канал в другой узел или покидает систему.

Таким образом, теорема Джексона утверждает, что в пакетной сети очередей каждый узел представляет собой не только независимую очередь с распределенным по Пуассону входным потоком, но и детерминированный поток в соответствии с принципами разделения, объединения и образования цепочек очередей.

Таким образом, каждый узел может рассматриваться отдельно от остальных при помощи схем М/М/1 или М/М/m. При этом средние значения времени задержки в узлах можно складывать. Время обслуживания запросов независимо, поскольку длина пакетов может изменяться при прохождении по контуру. Но, как показано Л.Клейнроком [3], и в случае одинаковых длин пакетов, предположение о независимых временах обслуживания вполне приемлемо, благодаря усредняющему эффекту объединения и разделения потоков.

Однако ничего нельзя сказать о величинах более высокого порядка. Но поскольку рассматривается пакетная сеть с большим числом абонентов-пользователей, то можно воспользоваться также результатом Центральной предельной теоремы, которая утверждает, что средняя величина от большого числа независимых случайных переменных (с конечными средними значениями и дисперсией) не зависит от их индивидуальных распределений и стремится к нормальному распределению Пуассона.

2. Метод временных задержек

Постановка задачи. Рассматривается сеть с коммутацией пакетов, состоящая из m узлов, соединенных K каналами передачи. Каждый узел действует как интерфейс для одной или нескольких присоединенных абонентских систем, а также как отправитель и получатель пакетов.

Внешняя нагрузка на сеть характеризуется следующим образом:

, (1)

где γ – суммарная нагрузка в пакетах в секунду; γ_jk – нагрузка между отправителем j и получателем k; N – суммарное число отправителей и получателей (абонентов сети).

Поскольку каждый пакет обрамляется заголовком и концевиком, другой служебной информацией («оверхед») и может на пути от отправителя к получателю преодолеть несколько каналов, суммарная внутренняя нагрузка будет выше внешней:

. (2)

Здесь λ – суммарная нагрузка во всех K каналах сети; λ_i – нагрузка в канале i; K – суммарное число каналов.

Внутренняя нагрузка зависит от фактического пути (контура) через сеть, по которому идут пакеты. Для любой услуги или некоторого приоритизированного трафика можно по параметрам сети и нагрузки определить среднее число линий (каналов), по которым пройдет пакет. Причем в зависимости от вида услуги U, можно найти среднюю длину контура q по формуле:

. (3)

Теперь задача заключается в определении величин средней задержки прохождения пакетов через сеть. Для этого можно воспользоваться формулой Литтла, которая справедлива и для сети очередей [2].

Для каждого канала i сети среднее число ожидающих и обслуживаемых запросов

r_i = λ_iτ_ri. (4)

Здесь τ_ri – временная задержка в каждой очереди, которую необходимо определить.

Суммируем эти величины и в результате получим среднее суммарное число пакетов, ожидающих во всех очередях сети.

Кроме того, среднее число пакетов в сети (обслуживаемых и ожидающих) выражается как γτ (также согласно формуле Литтла). Объединив эту формулу с (4), получим:

. (5)

Чтобы найти значение τ, нужно определить значения индивидуальных задержек τ_ri.

Поскольку предполагается, что каждая очередь рассматривается как независимая по схеме M/M/1, несложно вычислить, что

. (6)

Время обслуживания τ_si для канала i представляет собой отношение длины пакета b в битах (с учетом оверхеда) к скорости C_i передачи бит данных в секунду по этому каналу.

Таким образом,

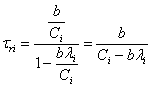. (7)

Собирая все элементы задержек вместе, подсчитывается среднее время задержки τ пакетов, отправляемых по сети:

. (8)

Тогда после преобразования средняя временная задержка Θ (в матричной форме) составит:

. (9)

3. Методология анализа производительности и качества МСОИ

Методология анализа производительности и качества МСОИ состоит из методики получения исходных данных, метода контуров, метода расчета временных задержек, методики выбора параметров МСОИ методом шагов по оврагу [4].

Ограничениями при анализе производительности МСОИ является соотношение β_d:β_t:β_v между числом различных абонентов-пользователей (Интернет, телефонии, потребителей видео/аудио контента) и стоимость (бюджет) D системы, причем

, (10)

где C_i – пропускная способность; d_i(C_i) – стоимость i-го канала.

В основу метода задержек положены контуры пакетов, математическая модель производительности, методика выбора параметров БС, алгоритмы автоматизированного расчета производительности [4], оценка временных задержек пакетов. Дополнительными в методе задержек являются определение стоимости оборудования БС МСОИ и топология размещения множества {БС}.

Максимальное число активных пользователей n, обслуживаемых с минимальной задержкой τ в сети очередей за временной период T, составит:

n = T/τ + 1, (11)

или, в общем виде, в матричной форме

N = T / Θ +1. (12)

Лемма. Интенсивность передачи в любом канале не может превышать произведения длины пакетов на реальную (с учетом оверхеда) интенсивность трафика (нагрузку).

Доказательство

После подстановки (9) в (12) получим

N= TГ^-1B^-1Λ^-1(C – BΛ)+ 1. (13)

Однако в пределе

T = BNμ^-1–Λ^-1, (14)

а при нагрузке, близкой к предельной, когда Λ^-1→0,

T ≈ BNμ^-1. (15)

Это дает

μ^-1Г^-1Λ^-1C = μ^-1Г^-1Λ^-1BΛ, (16)

и, сокращая, получим

C = BΛ. (17)

Это и означает, что интенсивность передачи в любом канале не может превышать произведения длины пакетов на реальную интенсивность нагрузки, или фактически

C < BΛ, (18)

что и требовалось доказать.

Выводы:

- каждый узел сети очередей может анализироваться отдельно от остальных при помощи схем M/M/1 и M/M/m;

- по исходным интенсивностям, или внешней нагрузке γ_jk (между отправителями j и получателями k), определяются фактические интенсивности, или нагрузка на отдельные каналы (λ_i), при необходимости и общая интенсивность Λ нагрузки на сеть;

- пакеты в контуре между отправителем и получателем могут проходить несколько узлов и линий связи (каналов), поэтому суммарная внутренняя нагрузка всегда выше внешней;

- средние задержки, определяемые по исходным интенсивностям для отдельных узлов и каналов сети и накладным расходам (оверхедам и контурам), складываются;

- результаты могут обрабатываться с помощью статистических методов.

Заключение.

Для анализа сети очередей оцениваются значения входных параметров нагрузки, а именно произведения средних значений интенсивности поступления запросов-пакетов (с учетом их оверхеда) на длину и допустимое время их обслуживания.

Для телефонного трафика известны голосовые кодеки (для видео тоже), поэтому ограничение допустимого времени обслуживания пакетов телефонии (видео) совпадает с периодом оцифровки голосовой (видео) информации t₀.

Однако при этом ничего нельзя сказать о моментах времени задержки более высокого порядка (например, о среднеквадратичных отклонениях).

Внутренняя нагрузка зависит от фактического маршрута (фаз контура) по сети, по которому идут пакеты, и от оверхеда пакетов (дополнительной информации: это - защитные интервалы каналов/подканалов и между пакетами, заголовки, концевики пакетов).

Предполагается, что для любого вида услуг по исходным параметрам нагрузки (виду контуров, входной и внутренней интенсивности, длинам пакетов) определяется количество узлов и линий (фаз контура), по которым проходят пакеты.

Если создается новая система, то оценки могут быть основаны на анализе и оценке работающих базовых образцов. Часто для исследования доступна существующая система, которую необходимо модернизировать. Чтобы оценить параметры проектируемой сети, можно измерить текущую нагрузку, генерируемую каждым устройством.

В сети с коммутацией пакетов время обслуживания представляет собой время передачи данных, и поэтому оно пропорционально длине пакета. (В случае сети с коммутацией каналов и телефонного трафика время обслуживания – это время, в течение которого абонент занимает оборудование).

Литература

[1] Широков В.Л., Лысяков Ю.М. Временные задержки в сети микроЭВМ с шиной Q-bus // Иваново. Тезисы докладов всесоюзного научного семинара. "Локальные вычислительные сети: Опыт реализации и перспективы развития". – М.: МЦНТИ. – 1986. – С.84-88.

[2] Столингс В. Современные компьютерные сети. 2-е изд. – М.: Питер. – 2003. – 783 с.

[3] Kleinrock, L. Queueing Systems, Volume II: Computer Applications. New York: Wiley, 1976.