BC/NW 2008, №2 (13): 9.1
АЛГОРИТМ ПОСТРОЕНИЯ
ПАРАМЕТРИЧЕСКОЙ МОДЕЛИ ИЗМЕНЧИВОСТИ СУТОЧНОГО ТРАФИКА
Репин Д.С.
(Москва, Государственный
научно-исследовательский институт информационных технологий и телекоммуникаций
(ФГУ ГНИИ ИТТ "Информика"), Россия)
Рассматривается задача
статистического анализа суточной изменчивости интенсивности трафика в
корпоративной компьютерной сети. В качестве характеристики интенсивности используется значение, получаемое путем
усреднения за одну минуту общего количества
байт информации, проходящей через точку контроля, и выраженное в битах в
секунду. С математической точки
зрения соответствующая наблюдаемая
последовательность значений интенсивности представляет собой дискретный
случайный процесс (временнóй ряд). Существенно, что этот ряд относится к
категории нестационарных. В этой
связи представляется желательным предложить алгоритм детального анализа свойств подобного
нестационарного трафика и построения его параметрической модели, что может
быть, затем использовано, например, для
целей имитационного моделирования сети [1].
Анализ структуры и свойств
трафика, будем проводить на примере реализации,
изображенной на рис. 1. Очевидно, что
она содержит, по крайней мере две компоненты: детерминированную составляющую 
типа систематического дрейфа (тренда) и
стохастическую компоненту 
с некоторыми вероятностными свойствами.
В
первую очередь выделим детерминированную компоненту. Известны два основных
способа ее выделения: параметрическая аппроксимация функции 
и применение сглаживающего фильтра типа
скользящего среднего. При использовании параметрического
подхода предполагается, что вид функции , описывающей трендовую составляющую анализируемого
нестационарного процесса 
, известен с точностью до параметров q0, q1, …, qp, т.е. что = d(t; q0, q1, …, qp) + 
. Тогда задача сводится к задаче
оценивания неизвестных параметров q0, q1, …, qp по N наблюдениям временного ряда 
, t — дискретное время, соответствующее номеру отсчета. Данная
задача по сути является задачей получения регрессионной зависимости, детально рассмотренной в научной литературе по
математической статитстике [2].
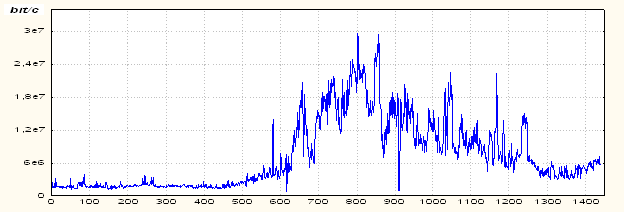
Рис.
1.
Попытаемся
построить параметрическую модель тренда в виде полинома четвертой степени.
Конечный результат в графической форме представлен на рис. 2.
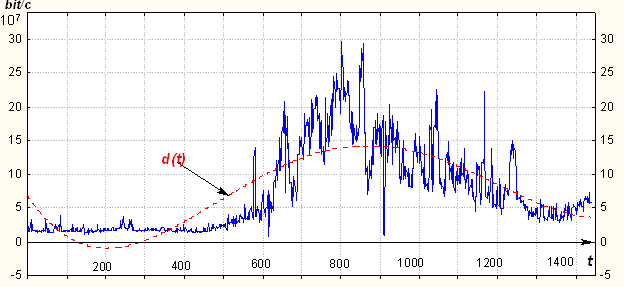Рис. 2.
Очевидно, что данная модель
тренда явно неудовлетворительна. Это, по-видимому, связано с достаточно сложной
и специфической формой трендовой кривой, где, в частности, присутствует
начальный участок с относительно низкой интенсивностью трафика. С практической
точки зрения, когда предметом наибольшего внимания является возможная перегрузка сети, временные
интервалы, с малой интенсивностью целесообразно исключить из рассмотрения.
Поэтому для дальнейшего анализа будем использовать данные для t = 570 – 1440 мин. Соответствующая параметрическая модель тренда по-прежнему
в виде полинома четвертой степени для указанного интервала изображена на
нижеследующем рис. 3. Очевидно, что она
достаточно точно отображает трендовую составляющую процесса .
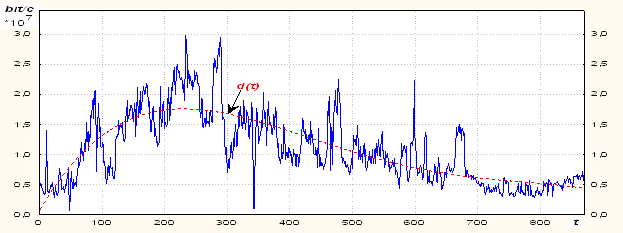Рис.
3.
Стохастическая компонента 
представляет собой разность (рис. 4):
= 
– 
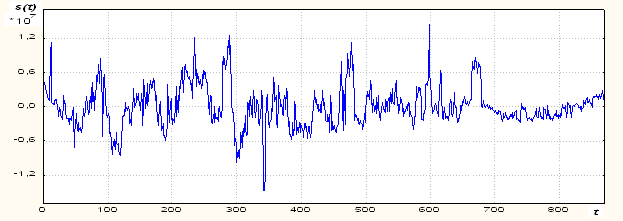Рис. 4.
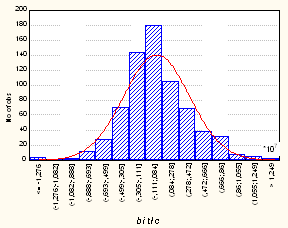
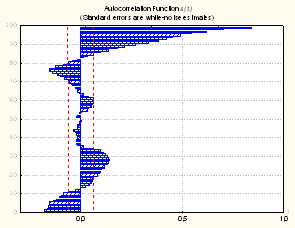
Гистограмма распределения
вероятностей и оценка нормированной корреляционной функции 
для указанного временного интервала
представлены соответственно на рис. 5а) и 5б).
|
|
|
|
а) |
б) |
Рис. 5.
Анализ приведенных рисунков показывает,
что, во-первых, можно с приемлемой
точностью считать распределение стохастической компоненты достаточно близким к
нормальному, а во-вторых, имеет место явная корреляционная зависимость между
ординатами этой компоненты. Это делает
перспективным получение адекватной параметрической модели процесса 
[2].
Действительно, удается получить адекватную модель авторегрессии 3-го
порядка АР(3) вида 
,
где 
; 
; 
. Остаточный процесс 
, образующийся
путем исключения из процесса 
авторегрессионной компоненты, должен иметь
корреляционную функцию типа 
-
функции, т.е. относиться к категории дискретного «белого» шума.
Полученные с помощью конкретного
примера результаты позволяют предложить общую схему (алгоритм) анализа
нестационарного трафика. Она включает в себя следующие элементы:
Ø
экспериментальное получение временнóго ряда изменения интенсивности
суточного трафика ;
Ø
выделение интервала анализа, в пределах которого интенсивность достаточно высока;
Ø
построение параметрической модели трендовой составляющей -например, путем ее аппроксимации полиномом
четвертого порядка;
Ø
выделение стохастической компоненты ;
Ø
оценивание и анализ одномерной функции распределения вероятностей и
автокорреляционной функции процесса ;
Ø
построение параметрической модели процесса - например, в виде модели авторегрессии
порядка p;
Ø
анализ свойств остаточного процесса ,
образующегося путем исключения из процесса
авторегрессионной компоненты.
В конечном итоге найденные в
соответствии с предложенным алгоритмом
параметрические модели компонент нестационарного трафика могут оказаться
полезными при анализе и прогнозировании
пропускной способности и эффективности использования элементов
корпоративной компьютерной сети.
ЛИТЕРАТУРА
1. Бахвалов Л.А., Репин Д.С.
Имитационное моделирование трафика в корпоративных компьютерных сетях. ХХХV Юбилейная
международная конференция «Информационные технологии в науке, образовании,
телекоммуникации и бизнесе IT + S&E’08». Украина, Крым, Ялта-Гурзуф, 20-30 мая
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы экономики. Учебник для вузов. – М.: ЮНИТИ,
1998. 1022 с.