BC/NW 2009; №2 (15):10.1
МОДИФИЦИРОВАННЫЙ МЕТОД КРИТИЧЕСКИХ РАБОТ В РЕШЕНИИ ЗАДАЧИ ПЛАНИРОВАНИЯ РАСПРЕДЕЛЁННЫХ ВЫЧИСЛЕНИЙ
Целищев А.С., Бобченков А.В., Емельянов Д.М.
(ГОУВПО «Московский энергетический институт (технический университет)», Россия)
При организации вычислений в распределённых средах возникает задача планирования и эффективного распределения ресурсов, осложняющаяся разнородностью состава и большим количеством наступающих событий, связанных с динамикой доступности ресурсов. Существующие планировщики вычислений чаще всего лишь частично поддерживают планирование вычислений для больших заданий с существенными зависимостями по данным между составляющими их задачами. Так, например, планировщик Maui [1] поддерживает описание составного задания только в виде простой очереди однородных подзадач с возможным назначением приоритетов и не осуществляет планирование с учётом возможных требований минимизации простоя ресурсов или оптимального их использования. В ситуации, когда простой ресурсов или использование быстродействующих вычислительных узлов равносильны потере времени или большим финансовым затратам (например, при условии взимания платы за использование ресурсов), подобные корректные расписания будут далеки от оптимальных.
Авторами предлагается подход к планированию распределённых вычислений, основанный на комбинации различных методов планирования и разрешения коллизий и позволяющий получать близкие к оптимальным расписания решений задач с учётом их структуры, разнотипности их подзадач, а также особенностей политики репликации и хранения данных в распределенной неоднородной среде с динамично изменяющимся составом вычислительных узлов, на которых выполняются эти задачи. Описанный метод позволяет применять различные комбинации критериев при оценке оптимальности расписания и подразумевает сохранение и выбор различных стратегий планирования (совокупностей расписаний для наиболее эффективного использования динамично изменяющегося состава ресурсов). В предыдущих работах ([2],[3],[4] и других) авторами были проведены исследования метода критических работ ([5]), предложены вспомогательные алгоритмы реализации метода, а также описаны особенности реализации системы моделирования планирования распределённых вычислений на их основе.
В настоящее время реализована и отлажена программная среда моделирования работы планировщика заданий с потоками случайно генерируемых сценариев распределённых вычислений. Имитационная модель позволяет формировать поток заданий от пользователей. Каждое из заданий представляется соответствующим параметризованным графом. Степень информационной связности вершин-задач может варьироваться. Число базовых процессорных узлов принимается кратным максимальной ширине яруса графа. Оценки длительности выполнения задач, объемов вычислений, времени доступа к данным – целые случайные числа, равномерно распределенные в заданном диапазоне. Конфликты между задачами, конкурирующими за один и тот же узел, разрешаются за счет незадействованных базовых узлов так, что обеспечивается минимум функции штрафа – например, суммы отношений объемов вычислений к оценкам длительности выполнения задач. Проверка более десяти тысяч случайно сгенерированных графов позволила рассмотреть ряд исключительных ситуаций и дополнить предложенные алгоритмы эвристиками, позволяющими увеличить вероятность нахождения близкого к оптимальному расписания выполнения каждого отдельно взятого задания.
Важно отметить, что реализованные ранее методы рассматривают упрощённую ситуацию наличия неограниченного числа ресурсов, не беря в расчёт их вероятную занятость другими задачами. В реальной ситуации планировщик должен учитывать информацию об ограниченности ресурсов, а выделяемый набор вычислительных узлов не всегда будет доступен в течение всего времени, отведённого на выполнение задания. Исходя из этого, авторами было принято решение модифицировать среду моделирования и дополнить методы планирования дополнительными функциями, которые позволят динамически выделять ресурсы и проводить планирование с использованием уже имеющихся наработок. Для решения этой задачи для начала необходимо хранить и динамически обновлять информацию о вычислительных узлах и интервалах их занятости.
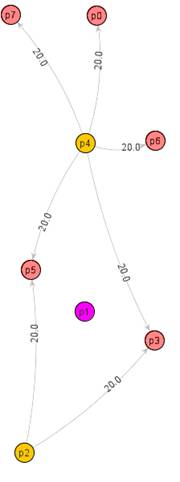
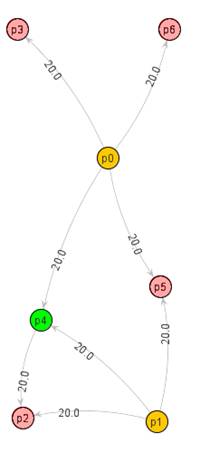
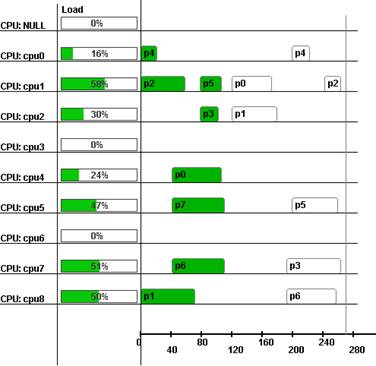
Рис. 1 Диаграмма двух непересекающихся заданий
Интуитивно понятен вид новых временных диаграмм, позволяющих отобразить планирование потока заданий во времени. Диаграмма, представленная на рис. 1, показывает выполнение двух заданий-графов на фиксированном наборе ресурсов, причём интервалы выполнения заданий не пересекаются (первый граф выполняется во временном интервале (0;110), второй – (120;270), ось абсцисс). Каждая строка в диаграмме показывает интервалы занятости соответствующего процессора соответствующими задачами в течение заданного интервала.
Отметим, что вид диаграммы близкого к оптимальному расписания для каждого задания обусловлен структурой этого задания и информационными связями между составляющими его задачами (см. левую часть рис. 1), а само построенное расписание обеспечивает близкое к оптимальному значение выбранной критериальной функции. Логично рассуждать, что поступление нового задания-графа в реальной системе может произойти в любой момент, более того, не исключена и ситуация одновременной подачи нескольких заданий, поэтому предлагается ввести следующие изменения в работу системы:
1. Вместе с информацией об информационных связях и наборе ресурсов подавать модулю планировщика времена высвобождения каждого ресурса (в общем случае массив слотов – интервалов простоя ресурса или массив интервалов занятости).
2. При рассмотрении планировщиком ситуации назначения задачи на определённый ресурс динамически формировать список доступных ресурсов.
3. При разрешении коллизий за ресурсы динамически формировать список доступных ресурсов.
4. С течением времени на каждом шаге моделирования обновлять информацию о текущем состоянии ресурсов.
Более подробного пояснения требует пп. 2, так как назначение и просчёт критериальных функций проводится в нетривиальных динамических циклах. При рассмотрении ситуации, в которой часть ресурсов занята под ранее распланированные задачи, модель среды метапланировщика становится динамической. Лежащий в основе работы алгоритм условной оптимизации изначально был предназначен для статической модели, не учитывающей начальное состояние системы. При этом количество единиц каждого ресурса принималось бесконечным. В реальных условиях, когда каждый ресурс уникален и частично зарезервирован (то есть доступен не в любой момент времени), исходный алгоритм не может быть применим, и планы, полученные в результате его работы, с высокой вероятностью будут приводить к неразрешимым коллизиям, что было установлено путем эксперимента. Очевидно, что для одной и той же критериальной функции и фиксированном наборе типов ресурсов одни ресурсы будут менее предпочтительны, а другие – наоборот. Внося же изменения в механизм вычисления критериальной функции на этапе планирования, можно перейти от рассмотрения методом критических работ не типов, а конкретных экземпляров ресурсов, получая, таким образом, близкое к оптимальному расписание для реального набора вычислительных узлов.
Для реализации описанной идеи было необходимо ввести временной курсор для вычисления начального момента планируемой задачи. Так как заполнение таблиц дерева поиска значениями критериальной функции производится на этапе "обратной прогонки" ([5]) в направлении от последней задачи критической работы к первой, то разумно в качестве временного курсора использовать запас времени на текущую задачу и следующие за ней (который является собственным параметром каждой таблицы в дереве поиска). Запас времени в данном случае рассматривается как отрицательное смещение относительно момента окончания критической работы, который нетрудно вычислить: либо он соответствует всему масштабу планирования для главной критической работы, либо определяется временем уже распределенной последней задачи в критической работе. При расчете начального момента планируемой задачи необходимо принимать во внимание все времена передачи, так как из-за особенностей алгоритма они не учитываются при поиске и перед планированием вычитаются из запаса на критическую работу.
Далее, при расчете критериальной функции необходимо найти оптимальный с точки зрения критерия ресурс, например, самый «медленный», исполняющий задачу не медленнее заданного времени T. При этом вводится дополнительный параметр tнач, определяющий планируемый начальный момент задачи и производятся следующие проверки:
- Ресурс не занят в момент времени tнач
- Ресурс не занят в момент времени tнач + T
- Ресурс не занят между моментами времени tнач и tнач + T
Данные об интервалах занятости ресурса, как уже было сказано, идут непосредственно на вход планировщика. В том случае, когда для варианта распределения задачи не находится подходящего ресурса по условиям критериальной функций, её значение устанавливается ошибочным, и таким образом оно не участвует в поиске условного оптимума.
Путем экспериментальных проверок было установлено, что варианты распределения, выдаваемые планировщиком при условии частично занятых ресурсов, не являются в общем случае подмножеством вариантов, получаемых при свободных ресурсах. Таким образом, планирование при ограничениях ресурсов и применение динамической модели для планировщика является оправданным и не может быть осуществлено только разрешением коллизий, при котором формирование массива ресурсов-кандидатов ([2]) происходит по аналогичной схеме.
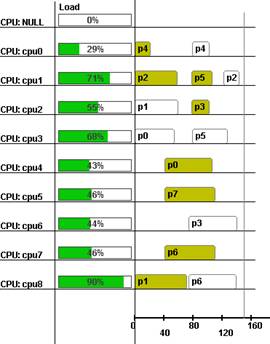
Рис. 2. Диаграмма двух пересекающихся заданий
Последняя версия среды моделирования метапланировщика, разрабатываемого авторами, поддерживает возможность получения и обработки заданий-графов в любой момент времени и осуществляет планирование с учётом информационных связей и доступности ресурсов по описанной методике. Возвращаясь к рис. 1, можно рассмотреть ситуацию, когда второе задание подаётся сразу после распределения первого (рис. 2). При применении модифицированного метода критических работ стало возможно проводить составление расписаний с учётом занятости ресурсов и, таким образом, уплотнять общее время выполнения потока заданий и увеличивать общее время занятости ресурсов (что в рассматриваемой модели является одним из критериев эффективного использования вычислительных узлов).
Таким образом, полученные нами результаты позволяют считать, что описанная разработка вплотную подходит к решению задачи создания планировщика, который позволит составлять близкие к оптимальным планы для связанных по данным сложно структурированных сценариев распределённой обработки данных с учётом динамического состава ресурсов.
На сегодняшний день, когда важность эффективного использования распределённых ресурсов необычайно высока, очевидно, что успешное завершение разработки авторов позволит создать мощный инструмент, позволяющий избежать значительных экономических потерь – как временных, так и финансовых - в самых различных областях деятельности.
Работа выполнена при финансовой поддержке РФФИ (грант 09-01-00095) и аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы» (проект 2.1.2/6718).
Литература
1.
www.clusterresources.com
2. Топорков
В.В., Целищев А.С., Бобченков А.В., Рычкова П.В. Метапланировщик – генератор стратегий распределённых вычислений.
Труды XV международной
научно-технической конференции "Информационные средства и
технологии". В 3 томах. Т.
1. - М.: Издательский дом
МЭИ, 2007.
3. Toporkov V. V., Tselishchev
A.S. Safety Strategies of Scheduling and Resource Co-allocation in Distributed
Computing. // Proc. of the 3rd Int. conf. on Dependability of Computer Systems DepCoS-RELCOMEX 2008. 2008. IEEE CS. P. 152-159.
4. Топорков
В.В., Топоркова А.С., Целищев А.С. Стратегии коаллокаций
для решения больших задач в распределенных средах. Научный сервис в сети Интернет: решение
больших задач: Труды Всероссийской научной конференции (22-27 сентября
5. Топорков В.В. Модели распределённых вычислений. М.: ФИЗМАТЛИТ, 2004. 320с.