BC/NW 2009; №2 (15):10.3
СТРУКТУРНАЯ
ИНФОРМАТИКА: ЗАДАЧИ РАЗЛИЧЕНИЯ И ОПРЕДЕЛЕНИЯ СХОДСТВА РАСПОЛОЖЕНИЯ ФРАГМЕНТОВ В ГРАФАХ
Кохов В.А., Кохов В.В.
(ГОУВПО «Московский энергетический институт (технический университет)», Россия)
Структурная информатика – новый раздел информатики актуальный для изучения студентами в университетах [1]. В докладе выделены задачи различения расположения и определения сходства расположения фрагментов в графах и приведены методы их решения. Методы программно реализованы в АСНИ «GMW» и используется в учебном процессе МЭИ (ТУ) (www.graphmodel.com).
Приведем
формализованную постановку задач различения
расположения фрагментов графа. Пусть G –
обыкновенный граф (G =(V, E), |V|=p, |E|=q).
Обозначим через Âl(G) (Â(G)) множество помеченных
фрагментов (фрагментов) графа G, а
через fi lt, fj ltÎÂl(G) - произвольные помеченные
фрагменты типа t. Задача различения
расположения двух однотипных помеченных фрагментов f lti, f
ltj в графе G определяется следующими
параметрами:
![]()
где xt - отношение принадлежности
фрагментов к одной орбите t-группы
(Aut t(G)) автоморфного расположения фрагментов типа t.
Решение задачи DP1 сводится к установлению истинности утверждения:
![]()
t-группа индуцирована группой Aut(G), то есть группой
автоморфизмов вершин графа G. В табл.1 приведены
все автоморфизмы t-группы расположения цепей длины 2 и
орбиты t-группы для графа G (рис.1).
Первым обобщением в разнообразии видов задач DP1 является задача автоморфного разбиения множества фрагментов типа t в графе G с параметрами:
![]()
где F lt – множество помеченных фрагментов типа t, вкладываемых в G.
Таблица 1.
Все автоморфизмы t-группы
расположения цепей длины 2
|
Автоморфизмы |
Цепи длины
2 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
g1 |
(1,2,5) |
(1,2,6) |
(2,1,3) |
(2,1,4) |
(3,1,4) |
(5,2,6) |
|
g2 |
(1,2,6) |
(1,2,5) |
(2,1,3) |
(2,1,4) |
(3,1,4) |
(5,2,6) |
|
g3 |
(1,2,5) |
(1,2,6) |
(2,1,4) |
(2,1,3) |
(3,1,4) |
(5,2,6) |
|
g4 |
(1,2,6) |
(1,2,5) |
(2,1,4) |
(2,1,3) |
(3,1,4) |
(5,2,6) |
|
g5 |
(2,1,3) |
(2,1,4) |
(1,2,5) |
(1,2,6) |
(5,2,6) |
(3,1,4) |
|
g6 |
(2,1,4) |
(2,1,3) |
(1,2,5) |
(1,2,6) |
(5,2,6) |
(3,1,4) |
|
g7 |
(2,1,3) |
(2,1,4) |
(1,2,6) |
(1,2,5) |
(5,2,6) |
(3,1,4) |
|
g8 |
(2,1,4) |
(2,1,3) |
(1,2,6) |
(1,2,5) |
(5,2,6) |
(3,1,4) |
|
Орбиты t-группы расположения цепей длины 2 |
||||||
|
[(1,2,5),(1,2,6),(2,1,3),(2,1,4)] [(3,1,4),(5,2,6)] |
||||||
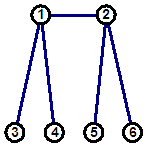
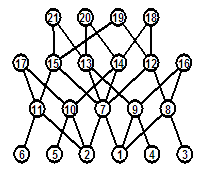
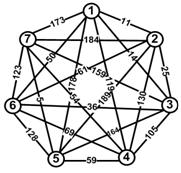
Рис. 1. Диаграмма графа, его трансграфа цепей и графа сходства
расположения цепей
Результатом решения задачи DP является построение орбит Aut t(G).
Следующий вид задачи различения связан с различением расположения
фрагментов f lti, f ltj типа t
относительно выделенного фрагмента f ltk того же типа t. Эта задача определяется
следующими параметрами:
![]()
где f lti, f ltj, f ltkÎF l t; x t – отношение принадлежности фрагмента к одной орбите фиксатора t-группы относительно фрагмента f ltk. Решением задачи DP2 является ответ на вопрос, связаны ли f lti и f ltj отношением x t, то есть, принадлежат ли f lti и f ltj к одной орбите фиксатора t-группы относительно f ltk . Обобщением задачи DP2 является задача автоморфного разбиения множества Flt относительно выделенного фрагмента f ltk с параметрами:
![]()
Обобщением задачи DP1 является задача различения расположения двух помеченных фрагментов f lt1i, f lt2j разных типов t1 и t2 в графе G. Она определяется следующими параметрами:
![]()
где f lt1iÎF lt1, f lt2jÎF lt2; x t1Ít2 – отношение вида «некоторый элемент орбиты помеченного фрагмента f lt1i изоморфно вкладывается в некоторый элемент орбиты помеченного фрагмента f lt2j», то есть
![]()
где Q( Aut t(G), f lt )
– орбита f lt относительно t-группы.
Обобщением задачи DP4 является задача различения расположения всех помеченных фрагментов типа t1 и t2 в графе G:
![]()
Заметим, что для решения задач DP4 и DP5 требуется сначала решить
две задачи DP (для фрагментов типа t1 и фрагментов типа t2).
Следующий вид задачи – задачи различения расположения f lt1i, f lt2j относительно выделенного фрагмента f lt2k типа t2 в графе G определяется следующими параметрами:
![]()
где x t1Ít2 – отношение вида «некоторый элемент орбиты расположения f lt1i изоморфно вкладывается в
некоторый элемент орбиты расположения f lt2j относительно фиксатора f lt2k для фрагмента f lt2j, то есть
![]()
Её расширением является задача различения расположения всех помеченных фрагментов типов t1 и t2 относительно выделенного фрагмента f lt2k типа t2 в G с параметрами:
![]()
Назовём все поставленные задачи классом задач различения расположения фрагментов (класс DPF). Заметим, что задача построения всех помеченных фрагментов графа, то есть поиск канонических изоморфных вложений фрагмента в граф G принадлежит классу NPC.
Нетрудно показать, что задачи различения графов
являются частным случаем задач DPF.
Действительно, пусть даны G1 и
G2. Построим граф H=G1ÈG2. Тогда задачи различения G1 и G2 можно рассматривать как
задачи различения расположения фрагментов типов t(G1)
и t(G2) в H.
Следовательно, верны следующие утверждения: (1) DP1 – обобщение задачи распознавания изоморфизма графов; (2) DP4 – обобщение задачи распознавания изоморфного вложения графа в граф; (3) Любая постановка задачи различения графов – частный случай некоторой задачи различения расположения фрагментов в графе. В табл.2 приведены обозначения задач, для трех подклассов задач различения, образующих класс инвариантного ядра задач в структурном спектральном анализе графов, который является теоретической основой структурной информатики [1]. В инвариантное ядро задач необходимо включить следующие задачи: (1) канонизация графа с построением канонической матрицы смежности графа; (2) канонизации представления помеченного фрагмента графа.
Рассмотрим основные подходы к решению задач различения расположения фрагментов в графе. Схема классификации основных подходов к решению задач различения представлена на рис.2. Алгебраический подход основан на использовании информации о строении конкретных групп автоморфизмов и задействует глубокие результаты прикладной теории групп. Используется в теоретических исследованиях. Переборно-групповой подход (ПП) использует переборные алгоритмы анализа Aut(G) и t-групп для получения точного решения задач установления x-эквивалентности. Структурно-характеристический подход (СХП) использует для различения различные инварианты. Этот подход объединяет переборные и не переборные методы.
Таблица
2.
Обозначения базовых задач из
инвариантного ядра задач различения
|
Обозначение |
Задача (вариант x-эквивалентности) |
|
Различение пары графов |
|
|
G1 » G2 |
Изоморфизм G1 и G2 |
|
G1 ÌS G2 |
Изоморфизм G1 подграфу G2
(вложение в смысле подграфа) |
|
G1 Ì G2 |
Изоморфизм G1 подфрагменту G2 |
|
Различение расположения пары
фрагментов типа t1, t2 |
|
|
f1l t » f2 l t |
Автоморфное расположение f1lt и f2lt ÎF lt(G) |
|
f lt1 ÌS f lt2 |
Расположение с вложением f lt1
в f lt2
как подграф |
|
f lt1 Ì f lt2 |
Расположение с вложением f lt1
в f lt2 как фрагмент |
|
Различение расположения пары
фрагментов относительно фрагмента f |
|
|
f1 lt »f f2 lt |
Автоморфное расположение f1ltи f2lt ÎF lt(G) относительно f l |
|
f lt1 Ì Sf f lt2 |
Расположение с вложением f lt1
в f lt2
как подграф относительно f l |
|
f lt1 Ìf f lt2 |
Расположение с вложением f lt1 в f lt2 как фрагмент
относительно f l |
Под непереборным понимаем такой инвариант, который для исследуемого класса графов строится за полиномиальное время. Трансграфовый подход имеет широкое применение особенно при решении практических задач различения расположения цепей в графах и путей в сетях. Его основой является ПП, а методы СХП обеспечивают сокращение перебора на основе использования определенных видов инвариантов.
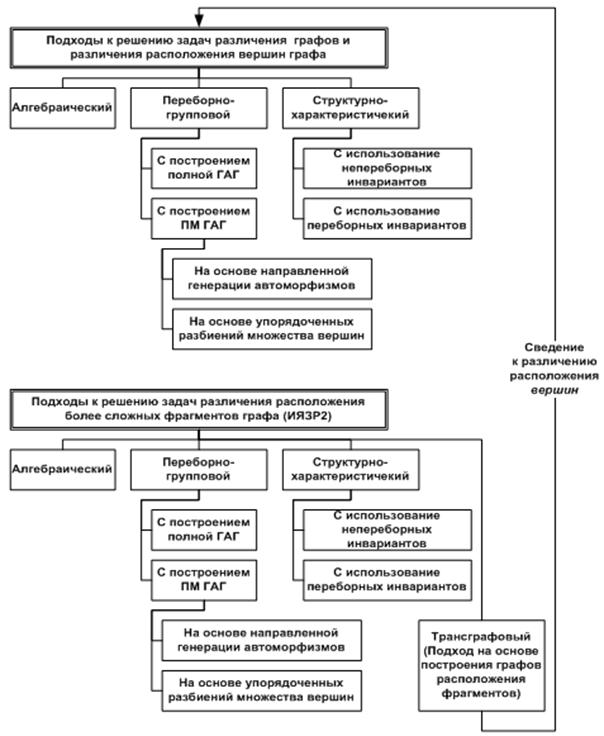
Рис. 2. Классификация подходов к решению задач различения графов и различения расположения фрагментов в графе
Многие результаты, полученные при исследовании СХП,
используются для повышения эффективности алгоритмов построения Aut(G)
(трансграфовый подход), а орбиты t-групп
служат для оценки точности полученных отношений t-эквивалентности.
Он позволил построить методологию иерархического уточнения расположения фрагментов
в графе, а ПП дал предел такого уточнения (орбиты t-групп). Приведем кратко метод, входящий в СХП, для решения задач
различения и определения сходства расположения фрагментов на основе b-моделей
[2]. В табл.3 приведена матричная форма b-модели
для графа G (рис.1), построенная на
основе достройки всех помеченных цепей G до фрагментов G, изоморфных элементам базиса из поддеревьев G.
Таблица 3.
Матрица b-модели и вклады фрагментов
в общую сложность графа
|
ISC(B) |
1 |
3 |
9 |
31 |
40 |
Irc(f tj) |
Irc(f t(c)) |
Irc(f t) |
|
Pl |
P0 |
P1 |
P2 |
P3 |
K1,3 |
|||
|
3,4,5,6 |
1 |
1 |
2 |
2 |
1 |
0.054 |
0.2179 |
0.4465 |
|
1,2 |
1 |
3 |
5 |
4 |
2 |
0.114 |
0.2286 |
|
|
13,14,25,26 |
0 |
1 |
2 |
2 |
1 |
0.050 |
0.2035 |
0.3017 |
|
12 |
0 |
1 |
4 |
4 |
2 |
0.098 |
0.0982 |
|
|
314,526 |
0 |
0 |
1 |
0 |
1 |
0.019 |
0.0394 |
0.2071 |
|
125,126, 213,214 |
0 |
0 |
1 |
2 |
1 |
0.041 |
0.1677 |
|
|
3125,3126, 4125,4126 |
0 |
0 |
0 |
1 |
0 |
0.011 |
0.0444 |
0.0444 |
|
Slw |
6 |
15 |
36 |
40 |
20 |
117 |
1 |
ISC = 279 |
|
Sw |
1 |
3 |
6 |
10 |
10 |
30 |
a(P0)
= 1 |
a(P1) = 1 |
|
WF |
6 |
5 |
6 |
4 |
2 |
23 |
a( P2) = 1 |
a(P3) = 1 |
Оценкой точности решения задач DP1 является «чувствительность» инварианта (значений b-модели) a(f lt/B, xt)=NC/NO, где NC – число классов эквивалентного расположенных фрагментов f lt по значениям b‑модели; NO – число орбит t-группы. Точное решение задачи DP1 на основе трансграфового подхода требует построения g-модели [2], например трансграфа цепей (рис.1) и определения орбит вершин в трансграфе цепей. Для получения точного или приближенного решения задачи DP1 для цепей необходимо построить b-модель для трансграфа цепей в базисе B. Чем длиннее базис, тем точнее результат решения задачи.
Результатом вычисления сходства расположения фрагментов в G будем считать граф попарных расстояний классов, эквивалентно расположенных фрагментов, то есть фрагментов с одинаковыми значениями строк матрицы b-модели. Иерархический анализ все более и более точного сходства расположения классов фрагментов G включает: (1) определение попарных расстояний между фрагментами на основе вычисления модуля разности индексов относительных вкладов (irc(f t(c))) в сложность; (2) определение на основе метрики Евклида расстояний между расширяемыми по числу элементов базиса значениями строк матрицы b-модели.
На рис. 1 приведен пример графа сходства расположения классов цепей.
Предложенные методы программно реализованы в АСНИ «GMW» и используются студентами МЭИ (ТУ) при изучении четырех дисциплин.
ЛИТЕРАТУРА
1. Кохов В.А. Основы структурной информатики. Тезисы докладов международной конференции «Информационные средства и технологии» международного форума информатизации МФИ-98, Т3. Москва, 1998. – С.42-47.
2. Кохов В.А. Концептуальные и математические модели сложности графов. М.: Издательство МЭИ, 2002. – 160 с.