BC/NW 2009; №2 (15):11.5
БИБЛИОТЕКА КЛАССОВ ДЛЯ ЭЛЛИПТИЧЕСКОЙ КРИПТОГРАФИИ
Белова А.Ю., Мамонтов А.И., Морозов С.В.
(ГОУВПО «Московский энергетический институт (технический университет)», Россия)
Работа выполнена при поддержке РФФИ, проект 08-01-00632а
Данная работа отражает опыт программной реализации операций различных алгебраических структур, на которых строятся современные криптографические протоколы. Описываются функциональность и принципы построения библиотеки классов AAL (Algebraic Abstractions Library), составляющей функциональную основу программного средства “Алгебраического процессор» [1]. Теоретическую базу функциональности библиотеки составляют теория конечных полей и теория эллиптических кривых [2,3]. При создании библиотеки AAL учитывались особенности построения современных библиотек такого класса, отраженные в статье [4], а также опыт создания библиотеки ECCMSUMPEI [2,3].
Общая характеристика
и функциональность библиотеки. AAL (Algebraic Abstractions Library) – это статически подключаемая библиотека
разработанная на языке программирования C++, использующая
стандартную библиотеку шаблонов для С++ STL (Standard
Template Library), и реализующая алгоритмы
операций алгебраических структур таких как:
- кольца Z целых чисел, Zn числовых вычетов и поля GF(p) простой характеристики p, p>3;
- кольца GF(2)[X] полиномов над бинарным полем, GF(2)[X]f(X) вычетов и поля GF(2n);
- кольца GF(3)[X] полиномов над тернарным полем, GF(3)[X]f(X) вычетов и поля GF(3n);
- поля GF(p2) - квадратичные расширения
простых полей простой характеристики
p, p>3;
- поля GF(24n), GF(36n) – расширения степени 4 и 6 полей GF(2n) и GF(3n);
- эллиптические кривые EC(GF(p)) над полями характеристики p, p>3;
- суперсингулярные и несуперсингулярные эллиптические кривые EC(GF(2n)) над полями характеристики два;
- эллиптические кривые EC(GF(3^n)) над полями характеристики три;
- эллиптические кривые EC(GF(p2)) над квадратичными расширениями простого поля характеристики p, p>3.
В AAL реализованы следующие алгоритмы:
- основных операций указанных выше алгебраических структур (сложение, умножение, аддитивное и мультипликативное инвертирование, деление, возведение в степень характеристики поля p в кольцах и полях, сложение, инвертирование и умножение на характеристику p поля в группе точек эллиптических кривых):
- возведения в степень в кольцах и полях, умножения на константу в группах точек эллиптических кривых;
- искажающих отображений и спаривания на различных эллиптических кривых для протоколов, основанных на спаривании [6].
- приведения по модулю (в различных кольцах);
- алгоритм Евклида в различных вариантах (основной, расширенный, бинарный основной, расширенный бинарный, расширенный для нахождения обратного элемента, расширенный бинарный для нахождения обратного элемента);
- генерации псевдослучайных последовательностей и параметров, в том числе и криптографически стойких;
- генерации образующих элементов и элементов высокого порядка:
- извлечения факторизации порядка мультипликативной группы из базы данных (используются при анализе примитивности многочленов, а также в функциях генерации оптимальных и гауссовых нормальных базисов);
- генерации и анализа простых чисел (вероятностные и достоверные тесты простоты, генерация больших простых чисел с заданными свойствами);
- вычисления символов Лежандра и Якоби;
- извлечения квадратного корня из квадратичного вычета по модулю простого числа и по составному модулю с известным разложением;
- решения квадратных уравнений над полем характеристики два;
- взятия точки эллиптической кривой, вложение данных в точку эллиптической кривой;
- извлечения квадратных корней в полях характеристики большей двух;
- вычисления хэш-функций и функции симметричного шифрования;
- генерации и анализа неприводимых многочленов[1];
- тестирования неприводимости, примитивности и базисности нормального множества;
- генерации неприводимых многочленов малого веса и анализа их свойств;
- генерации многочленов и таблиц умножения для оптимальных нормальных базисов и гауссовых нормальных базисов, алгоритмов перехода от нормального базиса того или иного вида к полиномиальному и от полиномиального базиса к стандартному;
- составления таблиц неприводимых многочленов над заданным полем, обладающих заданными свойствами;
- операций с матрицами и векторами (используются в функциях генерации и анализа неприводимых многочленов, а также в некоторых алгоритмах инвертирования);
- решения систем линейных уравнений над полями характеристики два и три;
Область применения библиотеки. Библиотека AAL достаточна для программной реализации:
- систем кодирования,
- криптографических систем с открытым ключом,
- криптографических протоколов в мультипликативной группе конечного поля,
- криптографических протоколов на эллиптических кривых.
Библиотека AAL может также использоваться в интерактивном режиме с помощью созданного когнитивного визуализирующего средства «Процессор МЭИ», входящего в состав программного средства «Алгебраический процессор»[1].
Методология разработки AAL. Основные идеи разработанной методологии позаимствованы из методологии разработки TDD(Test Driven Development) [7].
В её основе лежит следующая идея: «Перед написанием блока кода необходимо написать тест/тесты, которые этот код проверяют». То есть при разработке используется следующий подход – сначала тест, а потом код, который проверятся этим тестом, но не наоборот. Например, пусть необходимо написать метод, вычисляющий сумму двух чисел на языке C++ . Сигнатура метода будет выглядеть тогда следующим образом:
int sum(int a, int b);
Тогда перед написанием тела этого метода, то есть перед реализацией (интерфейс метода мы уже определили, о чем свидетельствует сигнатура, приведенная выше) мы должны написать тест, например, так:
void
testSum(void)
{int i=12,j=13;
alert(25 == sum(i, j)); }
Если теперь скомпилировать приведенную выше программу, то компилятор выдаст ошибку, говорящую о том, что метод sum не имеет реализации. Поэтому дальше необходимо реализовать метод сложения двух чисел, написав ровно столько кода, сколько заставит правильно работать написанный выше тест. Например, можно написать такой код:
int sum(int a, int b){ return 12+13;}
Ясно, что при такой реализации написанный выше тест
“сработает”, однако также понятно, что это неправильная реализация метода
сложения двух чисел, поскольку нарушено требование массовости (применимости к
варьируемым исходным данным). Напишем еще один тест
void test2Sum(void)
{int i=1,j=9; alert(10 == sum(i, j)); }
Теперь скомпилировав и запустив эту программу, на выходе снова получим ошибку. Это нормальный результат, который говорит о том, что реализация метода сложения двух чисел, предложенная выше, неправильная и необходимо изменить ее, чтобы заставить срабатывать все написанные тесты. Реализация, удовлетворяющая написанным в итоге тестам, будет выглядеть следующим образом:
int sum(int
a, int b){return a+b;}
Теперь скомпилировав и запустив эту программу, можно убедиться в том, что оба теста корректно отработали.
В итоге получился метод реализующий сложение двух чисел и два теста, проверяющих корректность его работы. В будущем если обнаружится ошибка в текущей реализации сложения, перед ее исправлением необходимо расширить систему тестов тестом, фиксирующим ее и только после этого перейти к исправлению.
Описанный выше подход к разработке дает нам следующие ощутимые преимущества:
- Всегда можно посмотреть варианты использования
метода в тестах. То есть при использовании этого подхода осуществляется
документирование библиотечного кода, что
является обязательным требованием.
- Написанный и документированный код работает, по крайней мере, в ситуациях, рассмотренных в тестах. Тесты выступает в роли контракта между разработчиком инструментальной библиотеки и разработчиком, использующим написанный библиотечный код в своих прикладных программах.
- Если в будущем в коде метода обнаружится ошибка, то после ее исправления существующая функциональность метода не будет нарушена так, как есть два теста проверяющие ее работу. В результате в будущем можно изменять код метода, не беспокоясь за функциональность, которую метод предоставлял ранее. Это обеспечивает возможность будущей поддержки кода, в частности, другим разработчиком. Сигнатура метода получается приемлемой для дальнейшего использования другими разработчиками, по крайней мере, так, как ее использовал автор перед написанием метода.
- Написанные тесты могут выступать в роли проверочных для метода с такой же функциональностью, как тот метод, для которого они писались. Это свойство может быть полезным для проверки других инструментальных библиотек, предоставляющих схожую функциональность.
Среда для разработки AAL. Разработка AAL осуществлена на языке программирования C++, на этом языке должна осуществляться разработка методов при ее пополнении. При разработке используется фреймворк CppUnitLite (кроссплатформенный фреймворк для написания и автоматического запуска тестов, написанный на языке C++) для простого создания и дальнейшего автоматического запуска тестов (при каждой компиляции), которые в дальнейшем будут создаваться для новых методов. Фреймворк удовлетворяет следующим требованиям:
- обеспечение простоты при создании тестов,
- возможность автоматического запуска всех тестов с последующим простым и наглядным механизмом обнаружения не сработавших тестов,
- независимость от компилятора языка программирования C++, то есть фрейворк должен быть написан без использования нестандартных средств языка C++ специфичных для какого-то конкретного компилятора.
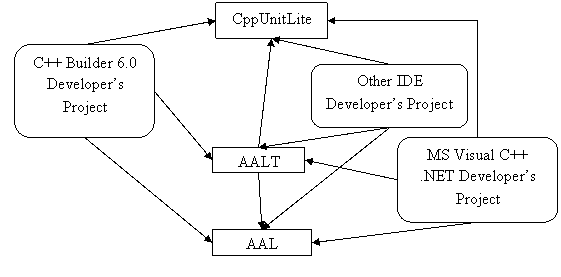
Рис. 1
Среда разработки состоит из:
- AAL – библиотека статически подключаемых классов, функциональные возможности которой описаны выше.
- CppUnitLite – фреймворк для создания и последующего автоматического запуска тестов.
- AALT – тесты для AAL, написанные при помощи CppUnitLite.
- Проекты разработчика. То есть проекты, составленные для конкретной интегрированной среды разработки IDE (Integrated Development Environment), которая в свою очередь поддерживает язык программирования C++ и STL.
Зависимости самостоятельных частей полученной среды разработки для инструментальной библиотеки AAL изображены на рис. 1.
Созданием такой среды для разработки инструментальной библиотеки AAL мы обеспечиваем независимость разрабатываемого кода от различных компиляторов для языка программирования C++.
Этапы разработки
новых методов для AAL. При разработке нового метода для AAL должна соблюдаться следующая
последовательность этапов.
1) Этап анализа. На данном этапе необходимо выполнить подробный анализ предложенного для реализации алгоритма. Перед реализацией алгоритма на языке программирования полезно также выполнить его реализацию на псевдокоде, чтобы убедиться, что понимание достигнуто и только после этого, непосредственно переходить к дальнейшему кодированию. Реализация на псевдокоде также пригодится при пополнении спецификации AAL для реализованного алгоритма.
2) Этап написания тестов. На данном этапе необходимо создать тест/тесты при помощи CppUnitLite, проверяющие работу метода/методов реализующих предложенный алгоритм и добавить их в AALT. При создании теста/тестов достаточно рассмотреть различные случаи входных данных, которые порождают собой различные варианты работы самого алгоритма.
3) Этап кодирования. На данном этапе необходимо добиться правильного срабатывания теста/тестов, написанных в предыдущем пункте, путем создания/модификации программной реализации предложенного алгоритма в AAL. В этом пункте нужно закодировать предложенный для реализации алгоритм по псевдокоду, полученному на самом первом этапе (этапе анализа), и затем убедиться в правильной работе по тестам, написанным на втором этапе (этапе написания тестов).
4) Этап обнаружения ошибки. Если в последующей эксплуатации реализованного алгоритма обнаружилась ошибка, необходимо вернуться к этапу написания тестов и дополнить их тестом, который олицетворяет найденную ошибку, после чего нужно опять перейти к этапу кодирования. Написание дополнительного теста предоставляет механизм проверки факта исправления ошибки, и страхует от появления таких ошибок снова.
Методика пополнения AAL. Для разработки AAL применяется система контроля версий исходного кода Tortoise SVN(Subversion), доступная через интернет для всех участников разработки инструментальной библиотеки AAL.
Для того чтобы воспользоваться системой достаточно установить приложение Tortoise SVN, создать папку, в которой предполагается вести работу, и выполнить команду Tortoise SVN SVNChecout, для того чтобы осуществить перенос кода из хранилища на локальную машину. Описанное действие необходимо выполнить один раз, в дальнейшем для того, чтобы получить актуальную версию кода из хранилища, достаточно выполнить команду SVN update, после чего на локальную машину будут перенесены изменения из хранилища, при этом переноса всего кода заново не происходит, и операция проходит достаточно быстро.
При пополнении AAL, чтобы корректно внести новый код в Tortoise SVN, необходимо выполнить определенную последовательность шагов. После выполнения описанных ниже шагов существующая функциональность библиотеки не должна измениться. Этот факт проверятся запуском всех существующих для инструментальной библиотеки AAL тестов.
Последовательность шагов при пополнении AAL следующая.
1) Первоначальный запуск тестов. Перед внесением, каких либо изменений в код инструментальной библиотеки и тестов, проверяющих этот код необходимо выполнить запуск имеющихся тестов и убедиться, что все тесты сработали верно. Для этого достаточно скомпилировать и запустить результат одного из проектов разработчика расположенных в папке $/MPEI_ASK/Dev_Project/, например, Microsoft Visual C++ Project. При существовании тестов, которые завершились неудачно, следует попытаться выяснить причины этих неудач. Если удалось выяснить причину неудачи и эта причина легко устраняется, то следует внести соответствующие изменения, после которых все тесты выполнятся правильно. Если же не удалось выяснить причину неудачи, или эта причина не является легко устранимой, то следует посмотреть с помощью команды show log приложения Tortoise SVN последнего разработчика, вносившего изменения и передать проблему ему, или же передать проблему ответственному за инструментальную библиотеку в целом.
2) Добавление тестов, проверяющих новый код и добавление нового кода инструментальной библиотеки
Выполнить команду SVN update, для того чтобы получить последнюю версию кода, убедиться, что внесенные изменения не вызывают конфликтов. Если имеются конфликты, то выбрав команду Check for Resolved, просмотреть различия в коде в специальном окне и, если возможно, разрешить конфликт, выбрав правильную версию, если решение не очевидно, то передать свой код ответственному за инструментальную библиотеку. Если конфликтов нет, то выполнить команду SVN Commit, в открывшемся окне в поле Message подробно описать внесенные изменения, в предложенном списке файлов отметить измененные файлы, не отмечая при этом служебные, и нажать кнопку Ok.
3) Конечный запуск тестов. Выполнить запуск имеющихся тестов (существующие до пополнения и добавленные во время пополнения) и убедиться, что все тесты сработали.
4) Последним шагом является пополнение спецификации инструментальной библиотеки. Необходимо внести спецификации добавленных методов, или изменить спецификации для существующих методов, интерфейсы которых поменялись. После того как описание составлено, необходимо добавить его в хранилище, для этого поместить его в папку Help, выполнить команду Add, после чего осуществить операцию добавления, как было описано выше.
Настоящая работа выполнена под руководством д.т.н. профессора Фролова А.Б.
Литература
1. Фролов А.Б. Гашков С.Б., Белова А.Ю., Морозов С.В., Жебет С.Ю., Щуров И.И. Программное средство «Алгебраический процессор». В кн. Информатизация инженерного образования: электронные образовательные ресурсы МЭИ. / Под общей ред. С.И.Маслова. - М.: Издательский дом МЭИ, 2008. Стр. 271- 274.
2. Болотов А.А., Гашков С.Б., Фролов А.Б., Часовских А.А. Элементарное введение в эллиптическую криптографию: Алгебраические и алгоритмические основы. - М.: КомКнига, 2006.
3. Болотов А.А., Гашков С.Б., Фролов А.Б. Элементарное введение в эллиптическую криптографию: Протоколы криптографии на эллиптических кривых. - М.: КомКнига, 2006.
4.
Волокитин М.В. Анализ алгебраических библиотек и основанных
на них программных средств. 17-я Международная Научно-техническая конференция
"Информационные средства и технологии". Москва, 2009. В наст. томе.
5. Чернышева Н.В. Программные средства тестирования и генерации многочленов с заданными свойствами над коечными полями. Доклад на XVI Международной научно-технической конференции «Информационные средства и технологии». Москва, 2008. Стр. 267-274.
6. Болдырев А.Г., Фролов А.Б. Функции спаривания в библиотеке классов для эллиптической криптографии, 17-я Международная Научно-техническая конференция "Информационные средства и технологии". Москва, 2009. В наст. томе.
7. Бек К. «Экстремальное программирование: разработка через тестирование. Библиотека программиста» - СПб.: Питер, 2003.