BC/NW 2009; №2 (15):2.1

 

ПОЛУКВАНТОВОЕ КОДИРОВАНИЕ В КОМПЬЮТЕРНЫХ КОМБИНАТОРНО-ТОПОЛОГИЧЕСКИХ МЕТОДАХ.

Рябов Г.Г.

(НИВЦ МГУ, Москва, Россия)

В основе конструктивного подхода к изучению многих явлений самой различной природы рассматриваются геометрико-топологические модели [2-7], на  которые опираются и в которые погружаются численные методы решения и характер которых во многом определяет выбор самих численных методов. Особое место среди таких моделей занимают решеточные модели, обладающие во многих случаях свойствами, инвариантными по отношению к размерности пространства, а среди них - решетка целых точек (точек с целочисленными координатами) Zn в евклидовом пространстве Rn с заданным ортонормированным репером е1,е2,..еn. Единичный n-мерный куб In в Rn обладает традиционным набором k-мерных граней (0≤k≤n), при котором грани 0 размерности – вершины (целые точки), грани размерности 1- ребра, грани 2-размерности-квадраты, грани 3-размерности-трехмерные кубы и т.д. до грани n-размерности-самого n-мерного единичного куба. Если распространить конструкцию In для всех целых точек Rn, то получим бесконечный кубический комплекс, который следуя  [8], будем обозначать Rnc  . Широкие исследования  кубических комплексов были инициированы С.П.Новиковым в 80-ые годы прошлого века. Этой тематике, в том числе  и отображениям на кубические структуры посвящены работы Деза, Штанько, Долбилина, Штогрина. Они заложили основу отношения к кубическим комплексам как к объектам, обладающим богатыми возможностями для эффективного отображения многих комбинаторных структур.[8,9] Целью предлагаемой статьи является рассмотрение нетрадиционных методов компьютерного представления (кодирования) и операций на кубических комплексах в Rnc., которые могли бы оказать влияние на архитектуру и состав операций будущих суперкомпьютеров, поскольку именно с суперкомпьютерными системами связаны надежды на решение многих комбинаторных задач.

 Кубанты и их свойства. На основе анализа рекурсивной процедуры вычисления коэффициентов пирамиды Паскаля в [10], установлено свойство биекции между множеством всех n-разрядных троичных кодов и множеством всех k-граней n-мерного единичного куба. Это позволяет ввести множество следующих конструктивных элементов, условно называемых кубантами (кубический квант). Такие элементы отражают с одной стороны геометрико-топологические свойства k-мерных граней ( кубов) в структуре n-мерного куба и  с другой стороны как n-разрядное слово с разрядами из алфавита {Ø,0,1,2} являются элементами алгебраической структуры-моноида (полугруппы с единицей) относительно специально введенной операции умножения, которая будет описана ниже.

Итак пусть в Rn задан ортонормированный базис е1,е2,…еn и пусть задано множество всех n-разрядных троичных слов {D} c разрядами di из алфавита{0,1,2}.Число таких слов равно 3n. Между номерами реперных векторов и номерами разрядов в словах установлено взаимно однозначное соответствие еiàdi. Пусть в слове D=d1,d2,…dn., часть разрядов принимают значения  2, часть разрядов 1 и остальная часть 0. Разрядам di1,di2,…dik, принимающим значение 2 ставится в соответствие декартово произведение единичных отрезков, коллинеарных реперным векторам ei1,ei2,…eik, т.е. k-грань в n-кубе. Остальные разряды со значениями 0 и 1 соответствуют отсутствию или наличию параллельного переноса (трансляции) по направлению реперного вектора, чей номер совпадает с номером данного разряда. Грубо говоря, троичный код отражает два действия-формирование k-грани около (0,0,…0) (разряды со значением 2) и трансляцию этой грани на «свое» место в n-кубе (разряды со значениями 0 и 1). Формально поэтому можно записать для k-грани F:

                                            F(k,x)=П ei    +  T  ej;

                                                          i:di=2;        j:dj=0,1

Отметим, что в принятой кодировке 0-грани (вершины n-куба) совпадают с общепринятыми координатами вершин единичного n-куба.

На рис.1а показана кодировка всех граней 3-куба (все кубанты в 3-кубе), а на рис.1б показан кубант 022211 (трехмерная грань в 6-кубе).

яр21a16

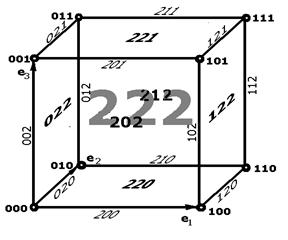
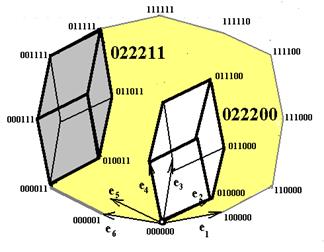
Рис.1 а).Все кубанты 3-куба, 222- весь 3-куб. б).Кубант 022211, как трехмерная грань в 6-кубе 022200, транслированная на 000011 (вдоль е5 и е6).

 

 Два кубанта в n-кубе могут находиться в следующих положениях друг относительно друга:

1.     Не пересекаться –не иметь ни одной общей точки.(пересечение-пустое множество).

2.     Пересекаться- иметь одну общую точку (0-грань-тоже кубант), общее ребро (1-грань), общую 2-грань и т.д., т.е. пересекаться только по кубантам. В частности один кубант может быть целиком частью другого кубанта.

Для определения (вычисления) пересечения                       х  |  0   1   2

 кубантов вводится операция умножения,                          ----------------

 которая является поразрядной и задается                            0 |  0  Ø   0 

 следующей таблицей.                                                            1 |  Ø  1   1

Здесь алфавит {0,1,2} дополняется                                       2 |  0   1   2

символом пустого множества Ø. И таким

 образом общий алфавит - {Ø,0,1,2}.

Следовательно появление в произведении двух кубантов по крайней мере в одном из разрядов Ø означает, что эти кубанты не имеют пересечения. Отсутствие в разрядах произведения Ø показывает, что кубанты образуют связное множество и сам результат умножения есть общий кубант (общая грань). В дальнейшем будет использована для обозначения произведения кубантов префиксная форма. Так произведение кубантов D1=220200 и D2=220211 будет записано: П(D1,D2)= 2202ØØ (пересечение отсутствует).             .

В расширенном четверичном алфавите слова соответствуют реальным k-граням без разрядов со значением Ø (кубанты) и не соответствуют граням в случае наличия в их разрядах Ø (псевдокубанты). Однако будем рассматривать их часто совместно, поскольку они вместе образуют полугруппу с единицей - моноид. Как нетрудно видеть такой единицей в моноиде является кубант 22…2.

Отметим, что длина минимального пути (по ребрам, т.е. по 1-граням, имеющим длину равную 1 ) между двумя непересекающимися кубантами в n-кубе равна числу разрядов со значением Ø в произведении этих кубантов. Будем обозначать эту величину через ω. Так в выше приведенном примере ω(П(D1,D2))=2 и Lmin(D1,D2)=2. В случае вершин n-куба длина минимального пути совпадает с хэмминговым расстоянием между соответствующими двоичными кодами.

Множество кубантов можно рассматривать как кубический комплекс в n-кубе, свойства которого (связность, структура дуального комплекса, отношения с другими комплексами) вычисляются алгебраически прежде всего на основании свойств моноида.

Кубический комплекс в n-кубе в общем случае может и не обладать свойством выпуклости, поэтому наиболее естественна  хаусдорффова метрика, которая является обобщением хэмминговой метрики между двоичными кодами. Хаусдорффова метрика (H-метрика) между двумя кубантами определяется как

                                 pH(D1,D2)=Max{ Lmin(D1,D2*/D1),Lmin(D2,D1*/D2)},

где D1*/D2 и D2*/D1 - «сжатия» кубантов по отношению соответственно к D2 и D1, определяемые в соответствии с поразрядными действиями, задаваемые ниже приведенными таблицами.

 

 

Грубо говоря такое сжатие соответствует выделению в одном кубанте наиболее удаленной части (также кубанта) по отношению к другому.

Так для кубантов 6-куба D1=022211 и D2=112222 соответствующие D1*/D2=002211 и D2*/D1=112200 Отсюда:

                              Lmin(D1,D2*/D1)=ω(П(D1,D2*/D1))=ω(Ø122ØØ)=3;

                              Lmin(D2,D1*/D2)=ω(П(D2,D1*/D2))=ω(ØØ2211)=2;

                                                 pH(D1,D2)=max{3;2}=3;

На рис.2а эскизно (с убиранием деталей) показана эта ситуация в 6-кубе. На рис.2б показана ситуация для случая двух комплексов К1={D1,D2,D3,D4,D5,D6}; и К2=D7, где D1=220000; D2=112200; D3=111122; D4=000022; D5=002211; D6=221111; D7=122021. Применяя алгебраически вышеизложенные методы, легко установить циклическую структуру двумерного комплекса К1, Lmin(K1,K2)=1. Для этого примера рН(К1,К2)=2 (в частности для вершины 101001 из К2 и вершин 100000,111000,000001,001011).

1a15

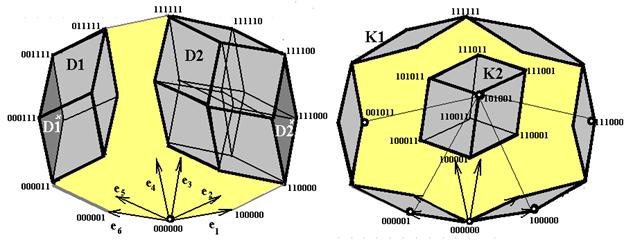
Рис 2. а).К вычислению хаусдорффовой метрики между кубантами D1 и D2 в 6-кубе, б).Взаимное положение комплексов К1 и К2 в 6-кубе; тонкими линиями соединены вершины, где реализуется рН(К1,К2)=2, как максимальное среди кратчайших между К1 и К2.

 

Итак кубанты n-куба образуют метрическое пространство с хаусдорффовой-хэмминговой метрикой. В [9] такие пространства отнесены к так называемым  гиперметрическим пространствам.

 

Кубические комплексы в Rnc. В данной работе мы остановимся только на одном, наиболее прикладном аспекте, подчеркивающем конструктивный характер предложенных методов кодирования. Но прежде вернемся к n-кубу и рассмотрим множество всех подмножеств (булеан) его кубантов, т.е. множество всех комплексов n-куба. Число элементов этого множества равно 2А, где А=3n. Кубант при выборе «машинного» алфавита {0,1,2,3}при замене (Øà0;0à1;1à2;2à3),можно рассматривать как число, записанное в четверичном  виде. Поэтому каждую строку из кубантов, соответствующую некоторому комплексу, можно выстроить в лексикографическом порядке, т.е. на первом месте в строке кубант с наименьшим числом и затем далее в порядке возрастания. С другой стороны каждому комплексу соответствует однозначно двоичный номер в булеане и значит все комплексы n-куба перенумерованы и каждый, как строка слов упорядочен.

Из этого общего построения мы воспользуемся частным случаем. При рассмотрении трехмерного случая ограничимся только двумерными кубантами, т.е. 2-гранями или просто квадратными гранями, число которых в 3-кубе равно 6. Тогда общее число комплексов только из таких граней (кстати гиперграней для 3-куба) равно 26=64 и весь булеан для этого случая представлен ниже вместе с нумерацией, а типы комплексов представлены на рис 3, где показано построение кубической бутылки Клейна из 2-комплексов, как из готовых панелей.

Комплексы, их кубанты и номера:

 

Ø-0;

1 кубант    (022)-1;(122)-2;(202)-3;(212)-4;(220)-5;(221)-6;

2 кубанта   (022,122)-7;(022,202)-8;…(220,221)-21;

3 кубанта   (022,122,202)-22;(022,122,212)-23;…(212,220,221)-41;

4 кубанта   (022,122,202,212)-42;(022,122,202,221)-43;…(202,212,220,221)-56;

5 кубантов (022,122,202,212,220)-57;(022,122,202,212,221)-58;…(122,202,212,220,221)-62;

6 кубантов (022,122,202,212,220,221)-63;

 

Собственно происходит отображение номеров соответствующих комплексов-панелей в трехмерный индексный массив памяти компьютера, где под каждый кубик 1х1х1 в данном случае достаточно одного байта (всего 64 различных номеров комплексов с учетом вращений комплексов вокруг осей симметрии 3-куба). Поскольку массив 5х3х5=75 байтам, можно говорить о бутылке Клейна «емкостью в 75 байт».

я31

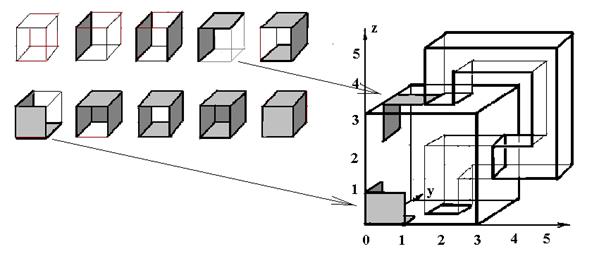
Рис.3.Кубическая бутылка Клейна из 2-комплексов-панелей емкостью 75 байт

 

Этот метод топологического панельного конструирования, показанный на этюдном примере, переносим на более высокие размерности.

 

Обсуждение результатов. Прежде всего отметим полиморфизм введенного кубанта, поскольку его можно рассматривать как:

1.Число в троичном или четверичном виде.

2.Геометрический объект- k-мерная грань в n-мерном кубе.

3.Топологический объект-элемент кубических комплексов.

Наиболее значимым представляется возможность представления многомерных кубических комплексов в троичном алфавите, а  с добавлением пустого множества в четверичном алфавите для образования моноида (алгебраической структуры) с введенной операцией умножения кубантов.

 Этот метод кодирования и единая операция над словами, совмещающими в своих символах существенно различные математические свойства, представляется как пример максимального (поразрядного) параллелизма.   

Рассмотрим некоторые вычислительные аспекты предложенных методов.

1.Релизация поразрядного умножения кубантов потенциально обладает неограниченным параллелизмом (точнее совмещением) при реализации на компьютере, поскольку ее можно рассматривать как логическое перемножение сколь угодно длинных четверичных (два бита) стрингов, которое может выполняться за один такт.

2.Введение хаусдорфова сжатия кубантов вместе с определением минимального пути между кубантами и комплексами переводит вычисление хаусдорфовой метрики из задач сложности 2n в разряд задач полиномиальной сложности. Это требует некоторого пояснения.

Пусть в In заданы два кубанта D1 и D2 размерности n/2. Тогда перечисление всех целых точек каждого кубанта ( для последующего вычисления max min L(D1,D2)) приведет к множествам размерности порядка 2n/2, в то время когда вычисления с хаусдорфовым сжатием требуют порядка n2 операций.

3.Перечисление и нумерация комплексов из гиперграней n-мерного куба могут быть оценены с точки зрения затрат памяти компьютера следующим образом.

 Для In число гиперграней (размерность n-1) равно F(k)= Ckn 2n-k при k=n-1, отсюда число различных комплексов на этих гранях равно 2F(k) и число разрядов под номера комплексов равно F(k). Для оценки емкости памяти в байтах обозначим через Fb(k)=F(k)/8 и размер решетки для отображения комплексов Xn. Таким образом объем памяти можно оценить как XnFb(k) и отсюда при оперативной памяти суперкомпьютера в 1015байт и Х=100 возможна работа для размерностей вплоть до 6d.

Заметим, что размерности 10d-11d, представляющие интерес в теоретической физике, при таких допущениях на емкость памяти допускают обработку решеток с Х=20-30.

4.Для оценки затрат машинного времени при обработке объектов высокой размерности будем исходить из режима одноразового прохода по решетке 1006 (для Z6) и замене в каждом шестимерном кубе номера комплекса в зависимости от содержимого соседних кубов (простейший вариант динамики при ближайшем зацеплении). Число операций такого локального преобразования положим пропорциональным числу соседних кубов-λ12. Отсюда перестройка комплексов при одноразовом проходе по всей решетке потребует примерно λ1013 операций и при   λ<100 оценка дает 1015 операций. Это дает возможность на современных суперкомпьютерах допускать многоразовые проходы на таких решетках для выявления тех или иных асимптотических тенденций перестроения комплексов. А в ряде случаев переходить к марковским моделям для установления эргодических свойств .[11].

 Конечно предположение столь простой линейной зависимости (λ<100) сугубо предварительно только для общей ориентации с ресурсами суперкомпьютера.

Отметим, что в развитие предложенного подхода естественно рассмотреть:

1.Возможность близкого подхода к кодированию симплициальных комплексов.

2.Действия симметрической группы  подстановок (и ее подгрупп) на кубанты.

3.Случайное троичное n-разрядное слово,  как случайный кубант в n-кубе и множество таких слов как случайный кубический комплекс с привлечением аппарата марковских цепей к анализу эргодических свойств случайных комплексов.

Предложенные методы развиваются в рамках инструментальной системы «Топологический процессор»[12], ориентированной на реализацию на суперкомпьютерах кластерного типа, в частности на суперкомпьютер МГУ «Чебышев» и суперкомпьютеры петафлопсного уровня.

Теперь о термине «полуквантовое» кодирование. Каждый разряд кубанта  может выражаться одним из символов 0,1,2. Если символы 0 и 1 соответствуют обычному двоичному алфавиту, то за символом 2 понимаются значения и 0, и 1, и весь отрезок действительных чисел, коллинеарный соответствующему реперному вектору. В этом смысле у символа 2 есть аналогия с q-битом из области квантовых вычислений [1]. Поскольку в кубанте присутствуют и те и другие разряды, то и был применен термин «полуквантовое» кодирование.

В заключение отметим, что в развитии суперкомпьютерного направления вместе с прогрессом в традиционных ресурсах - объеме памяти, числе процессоров, топологии их соединения, повышения тактовой частоты и т.д., заметную роль могут сыграть достижения алгебраической геометрии и топологии, теории категорий, трансформированные в новые формы кодирования и состав нетрадиционных  операций и предварительно отработанных на инструментальных системах.

Автор выражает благодарность за внимание и поддержку работы В.А.Садовничему, Л.Н.Королеву, А.В.Тихонравову.

Литература:

1.     Yu.I.Manin. Classical computing, quantum computing and  Shor,s factoring algorithm.//  arXiv:quant-ph/9903008v1 2Mar 1999.

2.     V.Kaibel, G.Ziegler. Counting Lattice Triangulations.// arXiv:math/0211268v2[math.CO] 13 Dec 2002.

3.     F.Lutz. Triangulated Manifolds with Few Vertices: Geometric 3-Manifolds.// arXiv:math/0311116v1[math GT] 7Nov 2003.

4.     P.Collet, J.Eckmann. Dynamics of Triangulations.// arXiv:math-ph/0412085v1 23Dec 2004

5.     F.Ardila, R.Stanley. Tilings.// arXiv: math/0501170v3[math.CO] 25Jan 2005

6.     V.Desoutter,N.Destainville. Flip dynamics in three dimensional random tilings.// arXiv: cond-mat/0406728v3 [cond-mat.stat-mech] 8Nov 2004

7.     J.Ambjorn, J.Jurkiewicz, R.Loll. The Universe from Scratch.// arXiv: hep-th/0509010v3 14Oct 2006.

8.     М.Деза, М.Штогрин. Вложение графов в гиперкубы и кубические решетки.//УМН.1997. т.52 №6.С.155-156.

9.     М.Деза, М.Штогрин. Мозаики и их изометрические вложения.// Изв.РАН. Сер.матем.2002.т.66№3.С.3-22.

10.             Г.Рябов. О путевом кодировании k-граней в n‑кубе//Вычислительные методы и программирование. 2008. т.9 №1. С.16-18

11.             Г.Рябов. Марковские цепи в динамике примитивной триангуляции в пространствах R3 и R4.//Вычислительные методы и программирование.2009.т.10№1.С.1-8.

12.             Ryabov G.,Serov V. Simplicial-lattice model and metric-topological constructions.// Proc. of the IX Conf. on Pattern Recognition and Information Processing. Minsk. 2007. Vol 2.135-140.