BC/NW 2009; №2 (15):2.3

ФОРМАЛИЗАЦИЯ ЗАДАЧИ МИНИМИЗАЦИИ АППАРАТНЫХ ЗАТРАТ В СИСТЕМАХ ОБРАБОТКИ СИГНАЛЬНОЙ ИНФОРМАЦИИ РЕАЛЬНОГО ВРЕМЕНИ

Овчинников В.А.

(ГОУВПО “Московский энергетический институт (технический университет)”, Россия)

В настоящее время наблюдается тенденция к повышению сложности задач, решаемых вычислительными системами специального назначения, в частности, системами обработки сигнальной информации реального времени. К основным особенностям таких вычислительных систем можно отнести фиксированный, априорно известный набор решаемых задач по обработке информации, а также необходимость их решения в реальном масштабе времени. Этот факт, наряду с повышением сложности решаемых задач, требует эффективной организации параллельных вычислений в системах данного класса.

При выборе той или иной вычислительной системы для решения прикладных задач пользователи неизбежно сталкиваются с вопросом: насколько данная система удовлетворяет классу решаемых задач. Однако, опыт разработки вычислительных систем обработки сигнальной информации свидетельствует о том, что при проектировании их структуры возможность организации параллельных вычислений либо не принимается во внимание, либо рассматривается лишь в самом упрощенном варианте, не учитывающем потенциальный параллелизм отдельных алгоритмов обработки информации. Такой подход не всегда позволяет удовлетворить всем предъявляемым к вычислительной системе требованиям, в частности, требованиям к ее производительности.

При этом, даже первичная оценка алгоритмов обработки информации, применяемых, например, в оптико-электронных приборах астроориентации космических аппаратов по звездам [1], позволяет сделать вывод о возможности наличия в этих алгоритмах значительной степени параллелизма. Об этом свидетельствует хотя бы тот факт, что на различных этапах обработки информации рассматривается некоторое множество (мощностью от нескольких единиц до нескольких десятков) источников излучения, каждый из которых может обрабатываться в той или иной степени независимо от остальных.

Следовательно, для оптимальной организации параллельных вычислений в такого рода системах, необходим метод, позволяющий в полной мере учитывать параллельную структуру применяемых алгоритмов обработки информации на этапе проектирования вычислительной системы. Учитывая специфику рассматриваемых вычислительных систем, вышеупомянутый метод оптимизации должен быть прежде всего направлен на:

- минимизацию времени решения возложенных на вычислительную систему задач;

- повышение эффективности использования (загруженности) аппаратных ресурсов вычислительной системы.

Существующие методы, направленные на решение задачи синтеза структуры вычислительной системы под выбранный класс задач, являются в той или иной степени эвристическими и не гарантируют получения оптимального решения для произвольного класса задач.

В связи с этим актуальность приобретает задача разработки метода синтеза структуры вычислительной системы, ориентированного не на применение различного рода эвристик, а, прежде всего, на формальный анализ параллельной структуры применяемых алгоритмов обработки информации. Такой подход, в отличие от эвристического, позволит получать результаты, применимые не только для задач обработки сигнальной информации, но и для произвольного набора алгоритмов обработки информации, используемых в проектируемой вычислительной системе.

Так как задача синтеза структуры вычислительной системы, на решение которой направлен разрабатываемый метод, является задачей оптимизации, то, прежде всего, необходимо решить вопрос о составе критериев оптимальности (f_i) и ограничений (g_i), накладываемых на получаемые решения.

Для ответа на этот вопрос рассмотрим следующую словесную формулировку задачи: для заданной модели поведения прикладной программы H и максимально-допустимого времени ее выполнения T_max необходимо спроектировать структуру вычислительной системы, характеризующуюся минимальными аппаратными затратами и обеспечивающую выполнение прикладной программы H за время, не превышающее T_max.

Из формулировки задачи непосредственно следует одно из ограничений:

Здесь t есть время выполнения прикладной программы H на ВС выбранной на очередном шаге поиска структуры HW_j. Прочие ограничения могут быть введены впоследствии, исходя из специфики системы обработки сигнальной информации, для которой проектируется структура ВС. В качестве таких ограничений можно рассматривать, например, минимально допустимую загруженность отдельных элементов ВС и ВС в целом, максимально допустимое количество тех или иных элементов ВС (модулей памяти, процессоров, линий связи), допустимые конфигурации коммуникационной среды и др.

Критерием оптимальности, в соответствии с приведенной формулировкой задачи, служит минимизация аппаратных затрат на построение ВС. Очевидно, что термин «аппаратные затраты» нуждается в уточнении. В работе [2] и ряде других публикаций предлагается ограничить термин «аппаратные затраты» лишь количеством процессоров ВС. Это, безусловно, упрощает процесс поиска оптимального решения, но предполагает, в частности, наличие полносвязной структуры коммуникационной среды, что не всегда является достижимым при практическом построении ВС.

Введение в рассмотрение других элементов ВС (памяти, коммуникационной среды) требует, с одной стороны, некоторого способа формального описания структуры ВС, а с другой — введения весовых коэффициентов, определяющих относительную значимость вклада элементов каждого типа в общие аппаратные затраты. Формальное описание структуры ВС может быть выполнено на основе классификации Д. Скилликорна [3] с введением следующего набора характеристик:

- количество процессоров (NP);

- количество модулей памяти с возможностью независимого одновременного доступа со стороны процессоров (NM);

- тип переключателя (коммуникационной среды) между процессорами (CP);

- тип переключателя между процессорами и модулями памяти (CM).

Очевидно, что при таком наборе характеристик, различным структурам вычислительных систем могут соответствовать одинаковые аппаратные затраты. То есть, требуется дополнительный критерий для определения какая же из структур с одинаковыми аппаратными затратами (разумеется, речь идет лишь о структурах, обеспечивающих выполнение ограничения (1)) является оптимальной. Таким критерием может служить оценка времени выполнения прикладной программы H на ВС структуры HW. Эту оценку времени можно либо рассчитывать лишь при нахождении нескольких оптимальных с точки зрения аппаратных затрат структур, либо, как предлагается в работе [4], включить в общий критерий оптимальности. Последний вариант является предпочтительным, так как с одной стороны не приводит к необходимости каких-либо дополнительных вычислений (так как оценку времени в любом случае требуется вычислять для проверки ограничения (1)), а с другой — позволяет учесть относительную значимость времени решения задачи и аппаратных затрат в каждой конкретной системе обработки сигнальной информации.

Один из возможных способов постановки и решения задачи синтеза архитектуры вычислительной системы под определенное приложение представлен в работе [2]: предлагается рассматривать задачу как смешанную многопараметрическую и многокритериальную экстремальную задачу с ограничениями в следующей постановке:

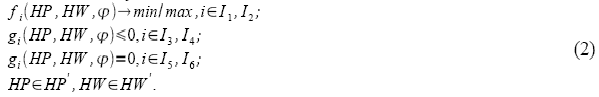
Здесь HP и HW — модели расписания выполнения программы и архитектуры ВС соответственно, j — оператор интерпретации, задающий взаимодействие между компонентами моделей HP и HW, f_i — критерии оценки качества решения, g_i — ограничения на допустимые решения, I₁, I₃, I₅ — множества динамических критериев и ограничений, I₂, I₄, I₆ — множества статических критериев и ограничений, (HP^', HW^') — пространство решений.

При такой постановке задачи оценки значений динамических критериев и ограничений для любого варианта решения (HP_j,HW_j) могут быть получены лишь после выполнения оператора интерпретации j, тогда как оценки значений статических критериев и ограничений можно вычислить непосредственно по моделям HP и HW без применения оператора j.

Так как для выполнения оператора интерпретации (а, следовательно, и вычисления оценок значений динамических критериев и ограничений) необходимо знание модели расписания выполнения программы HP_j на выбранной архитектуре HW_j, то на каждом шаге поиска оптимального с точки зрения архитектуры ВС решения задачи (2) требуется дополнительно решать задачу построения по возможности оптимального расписания организации вычислительного процесса. Этот факт с одной стороны приводит к возможности одновременного поиска ответа на оба вопроса, обозначенные в начале раздела, а с другой стороны обусловливает ряд недостатков предложенного в [2] метода, наиболее существенным из которых является то, что решать задачу построения расписания приходится на каждом шаге поиска оптимальной архитектуры ВС, хотя, в конечном счете, в качестве одного из компонентов решения задачи используется только расписание организации вычислительного процесса, построенное для выбранной на последнем шаге (оптимальной) архитектуры.

Таким образом, задачу (2) можно существенно упростить, исключив зависимость критериев и ограничений от расписания HP и оператора интерпретации j. Этого можно достичь либо отказавшись от применения динамических критериев и ограничений, либо переведя динамические критерии и ограничения в разряд статических, найдя способы вычисления оценок их значений, не связанные с построением расписаний. Последний способ является предпочтительным, так как потенциально не сужает класс решаемых задач и не снижает качество получаемых решений.

Из всего вышесказанного следует, что задачу оптимизации (3) можно сформулировать в следующем виде:

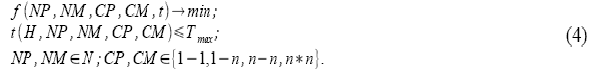
Здесь N — множество натуральных чисел.

Очевидно, что вычисление функции f из (4) при известных аргументах не представляет сложностей, а основная задача заключается в нахождении оценки времени t на каждой итерации поиска, а также в определении «направления движения» для следующей итерации.

При этом для эффективного поиска решения задачи (4) (в частности, вычисления времени t) необходимо выбрать метод описания модели прикладной программы H. Учитывая специфику решаемой задачи оптимизации, наиболее целесообразным представляется применение графовых моделей, позволяющих относительно легко варьировать уровень детализации при описании параллельного алгоритма, а также вводить в модель H сведения о времени выполнения отдельных операций и времени, затрачиваемом на пересылку результатов выполнения каждой операции через коммуникационную среду ВС.

Представление алгоритмов в виде объединения графов зависимостей, его описание с помощью набора покрывающих функций и применение математического аппарата разверток [3] дает возможность эффективного поиска решения задачи (4) непосредственно по записи алгоритмов, без построения расписания вычислительного процесса и без выполнения прикладной программы на реальной ВС

Учитывая такой выбор метода описания, основной задачей, требующей решения для получения оценок времени t из (4), следует считать разработку более эффективного (по сравнению с методами построения оптимальных расписаний) метода оценки времени выполнения алгоритма на вычислительной системе заданной структуры при условии заданного набора покрывающих функций графа параллельного алгоритма и некоторой развертки этого графа.

Литература

1. Абакумов В.М. Изделие 329К. Алгоритм работы изделия 329К. – М.: ОАО НПП «Геофизика-Космос», 2008.

2. Костенко В.А. Задачи синтеза архитектур: формализация, особенности и возможности различных методов для их решения. – Программные системы и инструменты. Тематический сборник. 2000, №1 – М.: МАКС Пресс, с. 31-41.

3. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2004.

4. Костенко В.А., Трекин А.Г. Влияние способа задания целевой функции на качество работы генетического алгоритма. – М.: Изд-во МГУ, 2000.