BC/NW 2009; №2 (15):4.3

 

ТЕНЗОРНЫЙ МЕТОД ПОСТРОЕНИЯ МОДЕЛЕЙ ПРОСТРАНСТВА ИНФОКОММУНИКАЦИОННЫХ СЕТЕЙ.

Кутергин В.А., Шадрин А.С.

(Институт прикладной механики УрО РАН)

 

Модель инфокоммуникационной сети (ИКС)

Сеть можно представить как систему, транспортирующую некий продукт из одной точки в другую. Этим продуктом могут быть люди, электроэнергия, природный газ, нефть и многое другое. Примером может служить система нефтепровода, где нефть течет из одной точки к другим точкам системы [1].

ИКС принято описывать с помощью графов - топология сети Гс задается графом G(N, L) [2]. Каждое ребро (ветвь) имеет длину, которая эквивалентна «стоимости» его использования, например, ее геометрической длине, пропускной способности, общей загрузке узла пакетами, передаваемыми по этой линии и т.п. В случае, когда учитываются направления ребер, задается ориентированный граф.

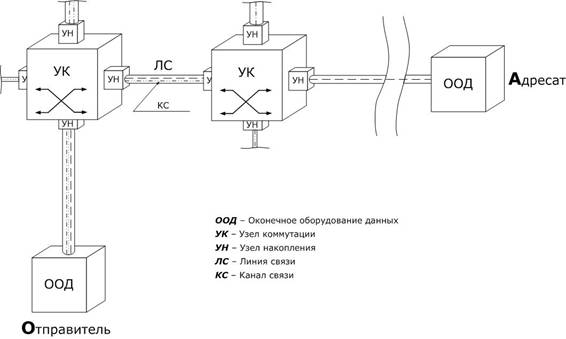
Рисунок 1 - Инфокоммуникационная сеть

 

Ребра графа представляют собой каналы связи, вершины – коммутационное и оконечное оборудование сети, соединяющее два или несколько входящих и исходящих каналов связи в требуемых направлениях. В целом задачу распределения информационных потоков выполняет система коммутации (см. рисунок 1), состоящая из собственно сети (КС), узлов коммутации (УК) и  системы подключения абонентов, реализованной в оконечных пунктах оконечным оборудованием данных (ООД). Наиболее важную роль в ней играют УК, обеспечивающие установление, поддержание и разъединение соединений между абонентскими терминалами (телефонными аппаратами, компьютерами и т.п.), каждому из которых присвоен адрес (номер).

Пусть КС характеризуются пропускными способностями, а УК - состояниями УН (узел накопления). Соотношения между значением информационного потока Λ [пакет/с], накопленным числом информационных пакетов V [пакет] и временной задержкой на передачу сообщений Т [с] описываются формулой Литтла [3]:

                                                                                            (1)

Будем считать, что сеть находится в сопредельном состоянии. В этом случае решение задачи эффективного распределения потоков информации в смысле минимизации времени ее доведения или потерь с ограничением по временной задержке, наряду с алгоритмом маршрутизации, существенно зависит от топологии сети. При этом потоки в сетях и структурное построение самих сетей являются взаимоопределяющими [2].

 

Объединение элементов в сеть, степени свободы и реакция связи

Связи, которые мы задаем между элементами системы — есть некоторые ограничения, которые мы накладываем на состояние или на параметры изменения состояния сети. Поскольку каждое состояние характеризуется определенным числом степеней свободы, то вводимые ограничения - связь, уменьшает это число степеней свободы или редуцирует их на такое число, сколько независимых уравнений относительно параметров состояния вводится для представления связей.

Если число степеней свободы несвязанных элементов сети N, а число уравнений связи равно т, то п = N-т есть число степеней свободы сети. В этой связи п - число независимых


параметров состояния сети; т - число независимых параметров - реакций связи, характеризующих влияние на поведение сети т независимых ограничений.

Введем N - мерное пространство LN с некоторой заданной системой координатных осей, которое можно поставить во взаимнооднозначное соответствие со всеми упорядоченными системами N действительных или комплексных чисел (λ1,...,λN). Каждой произвольной точке А этого пространства соответствует вектор, координаты которого (λ1,...,λN)А определяют пространство переменных состояния некоторой инфокоммуникационной сети.

Пусть на независимые параметры ИКС наложено  склерономных[1] связей, заданных системой независимых алгебраических уравнений:

                                                                                (2)

где ,  – матрица преобразования  

Пусть заданные источники информационных пакетов  определяют движение изображающей точки . В силу уравнений связи (2), траектория движения изображающей точки должна быть такой, что . Поэтому скалярное равенство элементов геометрических объектов  и  будет нарушено. В связанном движении кроме компонент  на изображающую точку будет действовать еще один источник движения -  в механике называемый реакцией связи: .

В ответ на введение связей (ограничения) возникает накопление информационных пакетов из-за свойств сопротивления в терминах времени элементов сети [4]. Поэтому геометрический объект - реакция связи   будет иметь свойства переменной числа информационных пакетов .

Переменная числа информационных пакетов непосредственно не задана, а зависит от характера движения изображающей точки  и свойств ограничивающей связи. Инвариантное уравнение поведения элемента сети, состоящей из однородных потоковых элементов в ковариантной и контравариантной форме, выведенное на основе формулы Литтла:

                                                                                     (3)

                                                                                  (4)

где ;  - матрица проводимости элементов сети.

Уравнения (3) и (4) можно сделать более симметричными, если дополнить их геометрическим объектом, который будет представлять воздействие на элементы сети источников информационного потока ; тогда уравнения (3) и (4) примут следующую инвариантную форму:

                                                                             (5)

                                                                             (6)

Рассмотрим представление полученных уравнений в новой системе координат  связанной со старой системой координат , преобразованием:

                                            (7)

Разобьем скользящий индекс  на два составляющих индекса , так чтобы . Тогда преобразования (7) можно записать в следующем виде:

                                                                   (8)

Данное преобразование не особое, поэтому для него существует обратное преобразование:

                                                                              (9)

где ;

 -  матрица обратного преобразования, .

Так как преобразование (9) произвольное и не особое, то уравнения с индексом  будут означать независимые координаты, а с индексом  будут представлять независимые уравнения преобразования координат таким образом, что в новой системе координат  уравнения связей (2) могут быть заданы в виде:

                                                                                                                                 (10)

и, следовательно, представляют  - мерную координатную плоскость пространства  (где  означает новую систему координат, в которой представлено подпространство ).

Теперь представим модель сети из взаимосвязанных потоковых элементов, подчиненных уравнениям связи (10) в системе координат . Для этого проделаем несколько этапов.

На первом этапе воспользуемся уравнениями (2 и 5), представив их в системе координат , связанной с исходной системой координат  преобразованиями (9). В результате получим:

                                                                    (11)

где  ;  ; ;  .

На втором этапе - воспользуемся разложением уравнений на два не пересекающихся множества, определяемых семантикой вектора , где  - независимые потоковые координаты;  - потоковые координаты, которые в силу уравнения (10) будут равны нулю, тогда уравнение (11) можно переписать следующим образом:

                                       (12)

где ; ; ; .

Введем обозначения:

 

Данные соотношения представляют собой элементы разложения метрического тензора по осям ξ, μ, φ, h. Тогда уравнения (12) примут вид:

                                                      (13)

Уравнения (13) представляют собой ковариантную форму модели ИКС в новой системе координат.

Однако в уравнение (13) не отражены уравнения связи (10), являющиеся дополнительными к уравнениям модели. Введение связей  приводит к тому, что  становится также равным нулю -  , где - множители Лагранжа [4].

Поэтому можно определить:

                                                                   (14)

поскольку  из условия ортогональности.

Уравнение (14) представляет собой аналог второго закона Кирхгофа, который индуцируется введенными уравнениями связей. Аналоги первого и второго законов Кирхгофа не являются независимыми по отношениями к модели ИКС. Введение связей в соответствии с аналогом первого закона Кирхгофа порождает такую структуру пространства ИКСN, в которой действуют оба закона как дополнительные друг к другу [4]. С учетом уравнения (14) модель ИКС из потоковых элементов может быть представлена в следующем виде:

                                                                                                                              (15)

                                                                                                                    (16)

где

Уравнения (15) позволяют определить n независимых контурных потоков , которые с помощью уравнений (16) позволяют рассчитать для  УН  объемов накопленных информационных пакетов . Посредством уравнений обратного преобразования контравариантных и ковариантных векторов можно определить значения и  для каждого элемента ИКС:

                                                                                      (17)

Уравнения (15) и (16) не единственные, которые можно использовать для определения  и . Из контравариантного уравнения представления ИКС (6), используя уравнения связи потоковых переменных (10) и следствия данных связей в виде реакций связей (14) можно получить следующую систему уравнений:

                                                               (18)

                                                                     (19)

Из системы уравнений (19) можно определить компоненты  подставив их в уравнения (18), получить значения компонент потоковых переменных .

Таким образом, введение связей топологически и физически означает появление  замкнутых контуров. Реакцией на введение связей является появление  контурных потоков и  уравнений связи  для контурных переменных.

В данной работе рассмотрен метод анализа параметров сложных сетей - использование методологии инвариантов и преобразований примитивной сети в модель инфокоммуникационной сети, имеющей заданную структуру связей. Данный метод может быть использован для решения задач моделирования сетей связи следующего поколения (NGN), а так же сетей передачи данных, находящихся в предельно нагруженном состоянии.

 

Литература:

1.               Андерсон Д. Дискретная математика и комбинаторика  // пер. с англ. – М.: Вильямс, 2003. 960 с .

2.               Пасечников И.И. Методология анализа и синтеза предельно нагруженных информационных сетей – М.: Издательство Машиностроение-1, 2004. 146 с.

3.               Швартц М. Сети связи: протоколы, моделирование и анализ. Часть I // пер. с англ. – М.: Наука, 1992. 336 с .

4.               Кутергин В.А. Искусственные объекты и конструкционные процессы – Ижевск, Издание УрО РАН ИПМ, 2007 г. 551 с.

 


[1] Склеромные – не содержащие время в явном виде