BC/NW 2009; №2 (15):6.2
ТЕСТИРОВАНИЕ БИБЛИОТЕК ОПРЕДЕЛЕНИЯ СТОЛКНОВЕНИЙ
Орлов Д.А.
(ГОУВПО «Московский энергетический институт (технический университет)», Россия)
Задача определения
столкновений трёхмерных объектов (collision
detection) [1] является неотъемлемой частью алгоритмов визуализации
трёхмерных сцен, как статических (САПР), так и динамических (тренажёрные
системы, системы мониторинга, компьютерные игры). На данный момент существует
множество реализаций алгоритмов решения данной задачи, оформленных в виде
программных библиотек: SOLID
[2], ColDet [3], OPCODE [4], COLLIDE [5]. Во многих библиотеках числа
представляются в формате с плавающей запятой, следовательно, результаты
арифметических операций над ними содержат ошибки округления. Для некоторых
алгоритмов вычислительной геометрии это может привести к получению качественно
неверного результата (например, получение невыпуклого
многоугольника вместо выпуклого, нахождение некоторых точек вне построенной
выпуклой оболочки), возможно
даже зацикливание алгоритма [6 – 8]. Подобные ситуации назовём вычислительными аномалиями. Тем не
менее, практически отсутствуют средства отладки, позволяющие определить
возможность возникновения вычислительных аномалий в программных реализациях
алгоритмов. В данной статье предлагается метод выявления возможности
возникновения вычислительных аномалий в библиотеках определения столкновений.
Введём следующие
определения. Предикатом вычислительной
геометрии назовём функцию, аргументами которой являются геометрические
объекты, а результат принадлежит конечному множеству значений. Примером может
служить предикат, вычисляющий ориентацию трёх точек на плоскости (где xi, yi – координаты точек, ![]() )
)
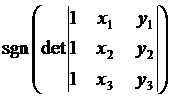
Если его значение
равно 0, то точки 1, 2, 3 лежат на одной прямой, если 1 – то точки
ориентированы против часовой стрелки, если -1 – то по часовой. Практически все
алгоритмы вычислительной геометрии используют предикаты. Так, один из
алгоритмов построения выпуклой оболочки множества точек, лежащих в одной
плоскости, использует описанный выше предикат. При вычислении предиката
вычислительной геометрии как правило формируется величина, исходя из значения
которой формируется выходное значение (путём сравнения с некоторыми константами
или определения знака числа). Если вычисления производятся в формате с
плавающей запятой, то рассматриваемая величина содержит ошибку округления (даже
в предположении, что его входные данные могут быть точно представлены в
соответствующем формате с плавающей запятой), следовательно, предикат может
вернуть неверное значение. Аналогично, если алгоритм содержит вычисление
функции, имеющей разрыв, то ошибки округления могут
привести к недостоверному результату
(график справа на рис. 1). Если f(x) – непрерывна, то ошибки округления
оказывают незначительное влияние на результат (график слева на рис. 1).
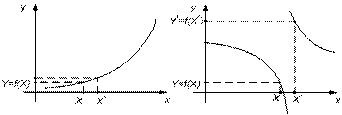
Рис. 1. Влияние ошибок
округления в случае непрерывной функции и функции, имеющей разрыв
Алгоритм
вычислительной геометрии может использовать объекты, построенные с
использованием существующих (например, вычислить точку пересечения двух
прямых). Координаты этих объектов также вычисляются с погрешностью, а значит,
могут нарушиться некоторые отношения между объектами. Топологической целостностью данных [7 – 8] назовём сохранение
использующихся в рассматриваемом алгоритме отношений между геометрическими
объектами. Например, для алгоритма построения выпуклой оболочки (на плоскости)
важно, чтобы для любых трёх точек из входного множества сохранялось отношение
ориентации. Вычислительная аномалия
(для алгоритмов вычислительной геометрии) – получение неверного результата
алгоритма (в случае, если алгоритм реализует предикат) или нарушение
топологической целостности выходных данных или зацикливание алгоритма. Таким
образом, причиной возникновения вычислительной аномалии является ошибка
округления которая, либо изменяет результат предиката, либо приводит к
получению недостоверного результата вычисления функции, имеющей разрыв.
Реализацию алгоритма будем считать подверженной
вычислительным аномалиям, если хотя бы для одного набора данных, точно
представимых во входном формате её аргументов, возникает вычислительная
аномалия.
В настоящее время
существует 2 подхода к определению столкновений: 1) приближённый: объекты
аппроксимируются телами, проверка на пересечение с которыми выполняется
значительно быстрее. В качестве подобных тел выступают сферы, параллелепипеды,
цилиндры, а также их объединения, организованные в деревья ограничивающих
объёмов [1]. Библиотеки, реализующие данный подход, жертвуют точностью в угоду
скорости, при этом они подходят для задач, где возможность возникновения
вычислительной аномалии не является столь критичной (например, для компьютерных
игр); 2) точный: на пересечение проверяются геометрические тела, представляющие
объекты. Однако, приёмы, описанные в предыдущем пункте, могут использоваться
для ускорения вычислений. Подобные библиотеки могут применяться как в графике
реального времени, так и в САПР.
В дальнейшем будем
рассматривать библиотеки реализующие подход 2), т.к. они должны давать точный
ответ на вопрос о наличии столкновения. Как правило, модели трёхмерных объектов
представляются в виде многогранников. Поэтому задача определения столкновений
сводится к задаче пересечения многогранников [1].
Разрабатываемый
метод тестирования состоит в решении модельной задачи для специально
подобранных наборов входных данных и сравнении полученных результатов с
эталонными. Это позволяет исследовать библиотеки без модификации их кода, в том
числе, доступные только в скомпилированном виде. Разработан алгоритм генерации
наборов входных данных для реализаций алгоритма определения столкновений, при
которых возможность возникновения вычислительных аномалий наибольшая. Для
библиотек определения столкновений в качестве модельной выбрана задача
определения взаимного расположения точки и плоскости, так как алгоритм её
решения достаточно прост, кроме того её можно переформулировать как задачу
пересечения двух многогранников: вершиной первого является исследуемая точка, а
грань второго принадлежит исследуемой плоскости. Модельную задачу будем решать
при следующих ограничениях: 1) плоскость задаётся уравнением в отрезках ![]() (где a, b, c – натуральные); 2) Ограничимся точками с
целыми координатами, для которых (0≤x≤2a; 0≤y≤2b). Тогда взаимное
расположение точки и плоскости определяется знаком выражения:
(где a, b, c – натуральные); 2) Ограничимся точками с
целыми координатами, для которых (0≤x≤2a; 0≤y≤2b). Тогда взаимное
расположение точки и плоскости определяется знаком выражения:
bcx+acy+abz-1 (1)
Поскольку данное
выражение может вычисляться в числах с плавающей запятой, его знак может быть
определён неверно только в случае, если его значение меньше (по абсолютной
величине) ошибки округления, с которой оно получено. Следовательно, необходимо
сгенерировать набор точек, для которых будет выполняться неравенство:
![]() (2),
(2),
где ε – оценка
максимальной погрешности, с которой может быть вычислено значение выражения
(1). Таким образом, в данном случае задача генерации подобных наборов данных
сводится к задаче решения семейства Диофантовых уравнений.
Проведён
эксперимент по определению подверженности библиотек определения столкновений (collision detection) вычислительным аномалиям. Проверялись следующие библиотеки: solid-3.5.6; ColDet 1.2. Также проверялись следующие реализации алгоритма
решения модельной задачи: с использованием целых чисел произвольной длины (эталонная реализация);
с представлением чисел в формате float; double. Получены следующие результаты: 1) все
исследованные реализации алгоритма (кроме эталонной) подвержены вычислительным
аномалиям; 2) разработан алгоритм генерации данных, при обработке которых в
реализации алгоритма определения столкновений, использующей вычисления с
плавающей запятой, велика возможность возникновения вычислительных аномалий; 3)
разработан алгоритм проверки библиотек определения столкновений на
подверженность вычислительным аномалиям.
ЛИТЕРАТУРА
1.
Christer
Ericson Real-Time Collision Detection, The Morgan Kaufmann, 2005
2. Сайт библиотеки SOLID http://www.dtecta.com/
3. Сайт библиотеки ColDet http://www.photoneffect.com/coldet/
4. Сайт библиотеки OPCODE http://www.codercorner.com/Opcode.htm
5. Сайт библиотеки COLLIDE http://www.cs.unc.edu/~geom/collide/index.shtml
6. L. Kettner, K. Mehlhorn, S. Pion, S.
Schirra, and C. Yap. Classroom Examples of Robustness Problems in Geometric
Computations // ESA, LNCS. 2004. Vol. 3221. P. 702—713.
7. http://www.mpi-inf.mpg.de/~kettner/pub/nonrobust_cgta_06.pdf.
8.
Орлов Д.А. Применение вычислений с исключением
ошибок округления для реализации алгоритмов вычислительной геометрии Труды XVI международной
научно-технической конференции «Информационные средства и технологии». 21-23
октября
9. Kokichi Sugihara. Robust Geometric
Computation Based on Topological Consistency