BC/NW 2009; №2 (15):8.1

ПРИМЕНЕНИЕ АППРОКСИМАЦИИ В ПРЕДИКТИВНОЙ СХЕМЕ СЖАТИЯ ИЗОБРАЖЕНИЙ

Чернов П.А., Гольцов А.Г.

(ГОУВПО «Московский энергетический институт (технический университет)», Россия)

Данная статья посвящена проблеме сжатия (построения компактного представления) полутоновых изображений в градациях серого. Изображение состоит из точек и представляется матрицей, элементы которой образованы одним числом, кодирующим цвет соответствующей точки. Полутоновое изображение – это изображение, которое удовлетворяет условиям:

а) для кодирования цветов точек используется достаточно много градаций (обычно более 64), что позволяет рассматривать цвет точек как непрерывную величину;

б) числовые представления цветов сравнимы, т.е. численно близкие коды означают близкие цвета, а чем разница больше, тем цвета сильнее различаются (контр пример - палитровые изображения, где численные представления цветов в общем случае сравнимыми не являются).

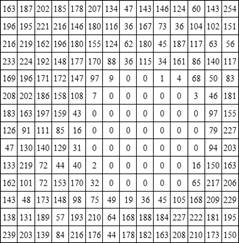
Пример полутонового изображения приведен на рис. 1.

Критерием качества решения проблемы является коэффициент сжатия – отношение размера сжатого представления изображения к размеру исходного представления изображения. Чем меньше коэффициент сжатия, тем лучше.

Известно, что в изображении характеристики близко расположенных точек сильно коррелированны, а модуль корреляции убывает по экспоненциальному закону с увеличением расстояния между точками [1]. Наличие данной корреляции указывает на избыточность исходного представления изображения. Одним из принципов сжатия, позволяющих использовать корреляцию соседних точек, является принцип предиктивного (предсказывающего) кодирования [2]. Задачей предиктора (блок метода сжатия, выполняющий предсказание) является предсказание характеристик точек. Примером простейшего предиктора является дельта-кодирование, когда результатом предсказания характеристик текущей точки является значение характеристик предыдущей точки.

Рис.1. Пример полутонового изображения (слева) и соответствующая ему матрица (справа).

Часто методы реализующие принцип предиктивного кодирования используют корреляцию точки, для которой выполняется предсказание, только с уже кодированными точками (рис. 2 (а)). Более совершенные методы предполагают проведение предварительного анализа сжимаемого изображения с порождением для различных его участков (как правило, прямоугольной формы) служебной информации предиктора (блок метода сжатия, выполняющий предсказание), позволяющей учитывать при выполнении предсказания для текущей точки характеристики точек, которые еще только предстоит кодировать.

Ставится цель улучшить сжатие полутоновых изображений, достигаемое при использовании принципа предиктивного кодирования. В качестве стратегии ее достижения принимается дальнейшее увеличение эффективности использования информации о точках, которые предстоит кодировать (рис. 2 (б)). В качестве источника дополнительной информации предлагается использовать аппроксимацию исходного изображения, полученную путем сжатия исходного изображения с потерями, например, методом SPIHT [3,4], который основан на вейвлет-преобразовании. Данный метод позволяет получать сжатое с потерями изображение очень близкое к исходному изображению даже при высоких степенях сжатия.

На практике улучшить сжатие по принципу предиктивного кодирования можно следующими способами:

а) повысить точность предсказания;

б) повысить точность моделирования ошибки предсказания.

Xi-2,j-2	Xi-2,i-1	Xi-2,j	Xi-2,j+1	Xi-2,j+2
Xi-1,j-2	Xi-1,i-1	Xi-1,j	Xi-1,j+1	Xi-1,j+2
Xi,j-2	Xi,j-1	Xi,j	Xi,j+1	Xi,j+2
Xi+1,j-2	Xi+1,i-1	Xi+1,j	Xi+1,j+1	Xi+1,j+2
Xi+2,j-2	Xi+2,i-1	Xi+2,j	Xi+2,j+1	Xi+2,j+2

(а)

Xi-2,j-2	Xi-2,i-1	Xi-2,j	Xi-2,j+1	Xi-2,j+2
Xi-1,j-2	Xi-1,i-1	Xi-1,j	Xi-1,j+1	Xi-1,j+2
Xi,j-2	Xi,j-1	Xi,j	Xi,j+1	Xi,j+2
Xi+1,j-2	Xi+1,i-1	Xi+1,j	Xi+1,j+1	Xi+1,j+2
Xi+2,j-2	Xi+2,i-1	Xi+2,j	Xi+2,j+1	Xi+2,j+2

(б)

Рис. 2. Качественная зависимость информативности точек из окрестности точки X_i,j, характеристики которой предсказываются, от их удаленности от точки X_i,j: (а) - в рамках предиктивного кодирования используются только уже кодированные точки, (б) – используется и аппроксимация. Более темный цвет соответствует меньшему уровню информативности точки.

Применительно для предсказания аппроксимацию можно рассматривать как результат работы дополнительного предиктора с вытекающими отсюда методами совмещения результатов работы предикторов. Другой подход - можно чередовать использование предикторов (различных типов, с различными параметрами) в зависимости от, например, активности области, на которой выполняется предсказание.

Считается, что линейные предикторы не в состоянии достаточно быстро адаптироваться к резко изменяющимся данным на контурах в изображении. Поэтому для содержащих контуры участков сжимаемого изображения целесообразно применять нелинейные предикторы [5]. Определить наличие контура в ходе процесса предсказания можно, проанализировав аппроксимацию, по которой, несмотря на допущенные потери, как правило, можно определить расположение контуров в исходном изображении. Определив по аппроксимации характер (активность) области исходного изображения, где проводится предсказание, можно чередовать использование линейных и нелинейных предикторов.

Для выделения в аппроксимации участков с различной активностью можно использовать математический аппарат кластерного анализа, и, в частности, метод k-средних [6]. Применение кластерного анализа к аппроксимации позволяет получать кластеры произвольной (не только прямоугольной) формы. Аппроксимация в равной мере доступна на стороне кодера и декодера, а значит, кластеризация на стороне декодера может быть повторена без накладных расходов в виде дополнительной служебной информации.

На этапе моделирования ошибки предсказания с помощью кластерного анализа можно выделить области изображения-ошибки, имеющие сходные статистические характеристики. Последовательное кодирование однородных данных позволяет снизить накладные расходы на адаптацию модели кодируемых данных. Кроме того, на основе данных об активности изображения в различных фрагментах изображения можно назначать качественно различные распределения плотности вероятности.

Открытым остается вопрос определения с каким коэффициентом сжатия лучше сжимать исходное изображение для получения аппроксимации, чтобы получить наименьший (или близкий к таковому) коэффициент сжатия без потерь исходного изображения.

ЛИТЕРАТУРА

1. Воробьев В. П., Грибунин В.Г. Теория и практика вейвлет-преобразования. – С.-Петербург: Военный университет связи, 1999, 203с.

2. Howard P.G. The Design and Analysis of Efficient Lossless Data Compression Systems // Brown University. Department of Computer Science. Technical Report No. CS-93-28 – 1993.

3. Pearlman W. A., Said A. Set Partition Coding: Part I of Set Partition Coding and Image Wavelet Coding Systems // Foundations and Trends in Signal 4. 4. Processing, Vol. 2, no. 2, pp. 95-180, Now Publishers, Delft, The Netherlands, 2008.

4. Pearlman W. A., Said A. Image Wavelet Coding Systems: Part II of Set Partition Coding and Image Wavelet Coding Systems // Foundations and Trends in Signal Processing, Vol. 2, no. 3, pp. 181-246, Now Publishers, Delft, The Netherlands, 2008.

5. Motta G., Storer J., Carpentieri B. Adaptive Linear Prediction Lossless Image Coding // Proceedings Data Compression Conference, IEEE Computer Society Press – 1999 – P.491 – 501.

6. Xu M. K-means Based Clustering and Context Quantization // University of Joensuu, 2005.