BC/NW 2010, №1 (16): 10.2

ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ СЛОЖЕНИЯ ЧИСЕЛ БОЛЬШОЙ РАЗРЯДНОСТИ

Нестеров А.П., Федулов А.С.

(Филиал ГОУ ВПО «МЭИ (ТУ)» в г. Смоленске)

На современном этапе развития компьютерной техники увеличивать производительность последовательных вычислительных машин становится все труднее и труднее. В таких условиях актуальным решением является использование параллельных вычислительных систем. В ряде областей (например, геофизика, обработка сигналов) используются операции над числами большой разрядности (ЧБР).

В данной работе исследуются способы распараллеливания сложения ЧБР.

Основной проблемой, которая затрудняет распараллеливание сложения ЧБР, является перенос, возникающий последовательно от младших разрядов к старшим.

В данной работе предложен метод организации параллельных вычислений при выполнении сложения ЧБР. Он основан на блочной обработке данных [1]. Предложенный метод заключается в следующем.

Предположим, что имеются p процессоров и C целых чисел, в записи наибольшего из которых имеется n цифр. Каждое число разбивается на k блоков (k>>p) по r разрядов. Блоки каждого слагаемого распределяются по процессорам, но все процессоры кроме первого получают дополнительно старший блок предыдущего процессора.

Все процессоры (кроме первого) определяют базовый входной перенос, и вычисляют две суммы блоков слагаемых (из-за использования блочной обработки входной перенос равен базовому или на 1 больше).

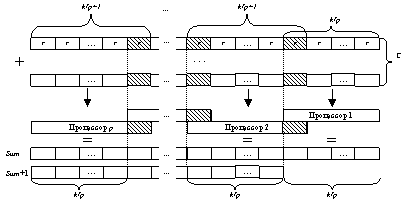
Рис. 1. Параллельная схема вычислений суммы чисел большой разрядности

Теоретические расчеты показали, что коэффициент ускорения алгоритма вычисляется по формуле (1)

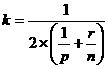. (1)

А общее количество выполняемых операций сложения по отношению к последовательному алгоритму определяется формулой 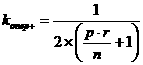(2)

. (2)

При увеличении разрядности слагаемых коэффициент ускорения стремится к p/2, а коэффициент увеличения количества операций сложения стремится к 0,5. Следует отметить, что данные коэффициенты не зависят от количества слагаемых.

Литература

1. Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. Учебное пособие – Нижний Новгород: Изд-во ННГУ им. Н.И. Лобачевского, 2003. 184 с.