BC/NW 2010, №1 (16): 7.5

Недвоичные линейные блоковые коды в цифровых системах связи с многоуровневой модуляцией

Петухова Е.В., Сушенцова Ю.В., Чернышев А.Ю.

МарГТУ, г. Йошкар-Ола

В цифровых системах связи (ЦСС) с целью обнаружения и исправления ошибок широко применяются линейные блоковые коды (ЛБК). Но на практике применяются в основном двоичные ЛБК. В то же время в современных ЦСС доминируют многоуровневые виды модуляции, в частности, N-ФМ и КАМ-N. В связи с этим актуальна задача исследования недвоичных кодов применительно к ЦСС с многоуровневыми видами модуляции.

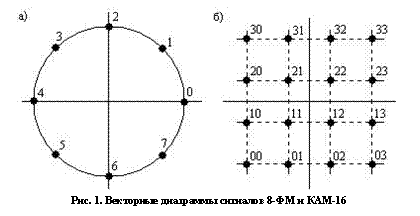
Принципиальная возможность сочетания многоуровневой модуляции и недвоичного кодирования продемонстрирована на рис.1 на примере сигналов 8-ФМ и КАМ-16. В первом случае ЛБК может быть задан в пространстве GF(8), а во втором – в пространстве GF(4). Выбор размерности конечного числового пространства в общем случае зависит от числа дискретных состояний модулированного сигнала и характера их распределения на векторной плоскости.

При анализе недвоичных ЛБК оценка кодовых расстояний производилась по методике, аналогичной оценке расстояний по Хэммингу, с допущением сворачивания векторной плоскости в цилиндры вокруг осей, что вполне согласуется с циклической замкнутостью конечных числовых полей относительно операции сложения по модулю M. Для многопозиционных ЛБК результирующее расстояние определялось как сумма частных.

При описании недвоичного ЛБК порождающей матрицей (ПМ), также определяемой в пространстве GF(M), кодирование выполнялось по правилу

где x_n – символы выходного кодового блока, b_k – символы входного информационного блока, g_kn – коэффициенты ПМ. При использовании в ПМ только единичных ненулевых коэффициентов значения минимального кодового расстояния (МКР) идентичны аналогичным двоичным кодам. В то же время установлено, что новые перспективы открываются при использовании ПМ с произвольными коэффициентами из множества элементов пространства GF(M). Например, ЛБК (4, 2), определенный в пространстве GF(4) и описываемый ПМ вида

,

обладает МКР, равным 4 (что недостижимо для двоичных ЛБК), при любых комбинациях остальных коэффициентов ПМ (g₁₁, g₁₃, g₂₂, g₂₄), составленных только из чисел 1 и 3.