BC/NW 2010, №1 (16): 9.3

ОПТИМИЗАЦИЯ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ И СКОРОСТИ ОБРАБОТКИ ДАННЫХ

(НА ПРИМЕРЕ МЕЖДУНАРОДНОГО КАЗАХСКО-ТУРЕЦКОГО

УНИВЕРСИТЕТА ИМ. А. ЯСАУИ)

Тукубаев З.Б., Умаров А.А.

г. Туркестан, Междунодный Казахско-турецкий

университета им. А. Ясауи, Казахстан

Одной из приоритетных направлений, является автоматизация деятельности  государственного аппарата, учреждений образования и культуры, ускорения реализации проекта "электронного правительства" [1,2]. Стоит подчеркнуть, что в разделе Цели – Показатели Стратегического плана развития вуза МКТУ им. А. Ясауи на 2009-2013 гг. [3, с. 72] определена конкретная цель – разработка информационной системы управления вузом.

Задача разработки и внедрения информационных систем (ИС) корпоративного управления состоит из нескольких этапов [4,5,6]. Как правило, речь идет о внедрении в вуз масштабных систем типа ERP (MRP) или прикладных систем, рассчитанных на большую организационную систему. Среди основных задач при разработке ИС можно выделить [6]:

1) изучение и анализ бизнес-процессов компании, фиксация бизнес-процессов, реинжиниринг процессов, если необходимо [14];

2) определение ключевых пользователей (автоматизированных рабочих мест) [14], их функции, обучение персонала в системе конкретных функции;

3) определение оптимального распределения потоков и оптимальной скорости обработки для настройки конфигурации системы;

4) внесение необходимых изменений в конфигурацию и настройки системы на основании результатов опытной эксплуатации; определение окончательного списка пользователей системы и фиксация ролей; запуск системы в промышленную эксплуатацию.

Задача исследования потоков заявок, поступающих на веб - сервер организации, в частности на центральный сервер МКТУ им. Ясауи описана в [16,17,18]. В работе был определен пуассоновский закон поступления заявок. Результаты, полученные в последних работах дают основу для настоящей задачи.  

Настоящая работа посвящается решению задачи 3 и состоит из двух подзадач:

- оптимизация распределения потоков по группам пользователей;

- оптимизация скорости обработки данных.

Эта задача на языке системного аналитика выглядит так; на основании качественного анализа характера транзакции /связей между ними, их типов и количеств/, которые обрабатываются ИС, определяются типы и параметры аппаратного обеспечения; будут определены используемые модули и основные параметры программного обеспечения, а также необходимое количество  задействуемых специалистов.

Существуют стандартные методы, позволяющие оценить параметры аппаратного обеспечения для достижения требуемого уровня быстродействия и надежности обработки данных. Привлечение экспертов по ИС позволяет определить, какую систему и какие конкретно модули необходимо использовать, каковы должны быть параметры базовой конфигурации. Необходимо отметить, что независимо от уровня компетенции специалистов однозначного ответа на этот вопрос не существует. При этом, возможно несколько альтернативных решений. Один из возможных подходов к выбору базовой конфигурации описан в [6]. Модели исследования производительности технических систем – сети, серверов рассмотрены в [9, 11, 12, 13, 18].

В конечном итоге, когда бизнес-процессы описаны, а также определены  конкретная система и ее модели, возникает задача: как распределить элементарные транзакции между К исполнителями (ключевыми пользователями и/или отдельными подразделениями). Критерием оптимальности  такого распределения обычно является поток информации (нагрузка и сложность операции), приходящие на одного исполнителя (задача 1), а также минимизация общего времени обработки информации (задача 2). В дальнейшем будем использовать максимально допустимый объем информации на одного исполнителя в единицу времени (в сек.)

Постановка задачи 1.

После анализа бизнес-процессов вуза можно определить понятие сложности бизнеса. Пусть всего в бизнес-процессах встречается N операции (элементарных транзакции). На основании накопленной статистики за квартал или год можно каждой операции   сопоставить относительную частоту ее появления , которая при выборке и устойчивых условиях деятельности будет стремиться к вероятности . Распределение потоков по группам пользователей (отделам) для Международного казахско-турецкого университета им. А. Ясауи представлен на рис. 1. Таким образом транзакция каждого типа характеризует частоту появления (статистическую вероятность), количество информации , и общий поток (объем)  информации, которую должна обрабатывать система управления в единицу времени. Задача баланса между и М  -мощностью системы управления – рассмотрена в работе [7].

Пусть определено К исполнителей (подразделений или пользователей). Обозначим через  – множество операций, выполняемых k-м исполнителем; Q={} – распределение операций по исполнителям. Будем называть допустимым такое разбиение, при котором удовдетворяется условие: , которое показывает что, отдел может обработать ограниченный объем информации в единицу времени. Кроме того, учтем что некоторые транзакции априори могут быть привязаны   к конкретным пользователям; т.е.: ,,– это правило определяется вопросами конфиденциальности информации (при этом, только конкретные пользователи авторизованы для работы с конкретными видами информации).

Введем обозначения для матриц. Для удобства изложения привяжем к каждой матрице таблицу:

№	Матрица	Назначение		Номер таблицы		Диапазон значений в Excel	Число элементов
	Входные матрицы
1.		Частота транзакции (вероятность распределения потока в месяц)		1		Лист1!A1:H30	8*30=240 (8 групп по 30)
2.	I	Количество информации в каждой транзакции		2		Лист1!J1:J30	1*30
3.	T TAU	Время выполнения каждой транзакции Время сокращения каждой транзакции		9		Лист2!B1:B30 Лист2!С1:C30	1*30 1*30
4.	E12	Матрица из 12 транзакции		5		Лист2! J1:U12	8*12
5.	Матрицы для промежуточных вычислений
6.			Объем потока информации в месяц	3		Лист3! A1:H30	8*30
7.			Объем потока информации в сек	4		Лист3! A1:H30	8*30
8.			Объем потока информации для выбранных 12 транзакции	12		Лист4! J1:U12	8*12
9.	K		Комбинаторные матрицы (для 12 транзакции)	6		Лист5!J1: J4096 Лист5!K1: KB4096 Лист5!L1: L4096 Лист5!M1: M4096 Лист5!N1: N4096 Лист5!O1: O4096 Лист5!P1: P4096 Лист5!Q1: Q4096 Лист5!R1: R4096 Лист5!S1: S4096 Лист5!T1: T4096 Лист5!U1: U4096	1*4096 (12 штук)
10.			Матрицы произведения для потоков (для 8 групп)	Нет		Лист6!A1: A4096 Лист6!B1: B4096 Лист6!C1: C4096 Лист6!D1: D4096 Лист6!E1: E4096 Лист6!F1: F4096 Лист6!G1: G4096 Лист6!H1: H4096	1*4096 (8 штук)
11.			Суммарная матрица распределения потоков без ограничений (для 8 групп)	7		Лист6!A4097:H4097	1*8
12.			Матрицы произведения для времени выполнения (для 8 групп)	Нет		Лист8!A1: A4096 Лист8!B1: B4096 Лист8!C1: C4096 Лист8!D1: D4096 Лист8!E1: E4096 Лист8!!F1: F4096 Лист8!G1: G4096 Лист8!H1: H4096	1*4096 (8 штук)
13.			Матрицы произведения для времени сокращения (для 8 групп)	Нет		Лист9!A1: A4096 Лист9!B1: B4096 Лист9!C1: C4096 Лист9!D1: D4096 Лист9!E1: E4096 Лист9!F1: F4096 Лист9!G1: G4096 Лист9!H1: H4096	1*4096 (8 штук)
14.			Суммарная матрица времени выполнения	13		Лист8!A4097: H4097	1*8
15.			Суммарная матрица времени сокращений	14		Лист9!A4097: H4097	1*8
16.			Максимум времени сокращений	Нет		Лист9!H4100	1 ячейка
17.	V12		Матрица разности	Нет		Лист10!A1: A4096 Лист10!B1: B4096 Лист10!C1: C4096 Лист10!D1: D4096 Лист10!E1: E4096 Лист10!F1: F4096 Лист10!G1: G4096 Лист10!H1: H4096	1*4096 (8 штук)
18.			Суммарная матрица скорости выполнения без ограничений (для 8 групп)	14		Лист10!A4097: H4097	1*8
19.	Выходные матрицы (результат)
20.	GM		Матрица распределения потоков с ограничением (для 8 групп)	Нет		Лист7!A1: A4096 Лист7!B1: B4096 Лист7!C1: C4096 Лист7!D1: D4096 Лист7!E1: E4096 Лист7!F1: F4096 Лист7!G1: G4096 Лист7!H1: H4096	1*4096 (8 штук)
21.			Суммарная матрица распределения потоков без ограничений (для 8 групп)	8		Лист7! A4097: H4097	1*8
22.	Конечный результат задачи 1 DISP		Дисперсия распределения потоков (Ф)	Нет		Лист7!D4100	1 ячейка
23.	Z12		Матрица ограничений (для 8 групп)	15		Лист10!A1: A4096 Лист10!B1: B4096 Лист10!C1: C4096 Лист10!D1: D4096 Лист10!E1: E4096 Лист10!F1: F4096 Лист10!G1: G4096 Лист10!H1: H4096	1*4096 (8 штук)
24.	Конечный результат задачи 2 SKOR		Суммарная матрица скорости обработки (для 8 групп)	16		Лист10!A4097: H4097	1*8
25.	Ограничения
26.	C=1 000 000		Ограничение на поток (бит)	Нет	Лист7!E4099		1 ячейка
27.	S=1800		Ограничение на время обработки одной группы (сек)	Нет	Лист10!E4099		1 ячейка

Данные

Таблица 1. Частота транзакции (распределение вероятностей) за 1 месяц ()

Тран Закции	Ректо рат	Уч отдел	Метод Отдел	Науч отдел	Библио тека	Дека нат	Препода ватели (10 факульт)	Студенты (10 тыс)	Всего	В %
ПОИСК студента по ФИО	513	1334	409	420	219	2861	4876	40256	50888	8,75
ПОИСК студента по специальности	461	1211	309	313	0	2603	4690	32302	41889	7,20
ПОИСК студента по группе	383	318	285	276	0	2777	3902	38184	46125	7,93
ПОИСК преподавателя по ФИО	525	546	2308	2211	0	2344	7954	38415	54303	9,34
ПОИСК преподавателя по предмету	320	493	1869	1624	0	1990	7112	36068	49476	8,51
ПОИСК преподавателя По фак/каф	363	417	1960	1883	0	2203	6612	34413	47851	8,23
ПОИСК номера приказа	1068	436	389	410	376	566	1003	0	4248	0,73
ПОИСК номера исх/вх. документа	1103	580	406	415	390	572	1022	0	4488	0,77
РАСЧЕТ колич. исх/вх. Документов	501	380	311	295	251	244	0	0	1982	0,34
РАСЧЕТ колич. обработ. документов /завершенных дел	486	566	330	399	283	233	0	0	2297	0,39
РАСЧЕТ колич. студ.  по вузу в разрезе на факультет	0	365	0	0	0	1862	2066	9311	13604	2,33
РАСЧЕТ баллов GPA студ. по группе	0	482	0	0	0	1607	3991	13022	19102	3,28
РАСЧЕТ общей нагрузка часов по факультету __	0	885	0	0	0	2334	2668	0	5887	1,01
РАСЧЕТ нагрузки препод вуза	0	742	0	0	0	3457	3435	0	7634	1,31
РАСЧЕТ общего расписания занятий по факультету	0	611	0	0	0	2360	0	0	2971	0,51
РАСЧЕТ расписания занятий у преподавателя	0	437	0	0	0	2991	3633	0	7061	1,21
ПОИСК Учеб – метод. пособий по автору ___	0	0	336	0	0	0	2010	4081	6427	1,10
РАСЧЕТ колич. опубл. уч. метод пособ препод. ___	0	0	301	0	0	0	1233	0	1534	0,26
РАСЧЕТ колич опубл. книг препод. ___	0	0	298	0	0	0	4077	0	4375	0,75
РАСЧЕТ оплаты студ. за год/семестр____	409	1076	0	0	0	2578	3340	30456	37859	6,51
ПОИСК статей по по направлению исслед. ___	0	0	0	563	886	0	0	3818	5267	0,90
РАСЧЕТ колич. опубл. статей препод. ___	0	0	418	0	0	0	1560	0	1978	0,34
РАСЧЕТ колич. опубл книг препод. ___	0	0	277	0	0	0	4099	0	4376	0,75
ПОИСК книг по автору  ___	0	0	560	528	1684	0	12605	15060	30437	5,23
ПОИСК книг по теме  ___	0	0	435	330	1479	0	13074	18848	34166	5,87
РАСЧЕТ колич. поступ книг	0	0	0	0	566	0	1306	2238	4110	0,70
РАСЧЕТ колич. книг у читателей	0	0	0	0	622	0	0	0	622	0,10
РАСЧЕТ числа читателей по вузу	0	0	0	0	470	0	0	0	470	0,08
РАСЧЕТ успеваемости в группе  ___	0	230	0	0	0	669	4683	39006	44588	7,66
РАСЧЕТ посещаемости в группе  ___	0	314	0	0	0	891	5879	38283	45367	7,80
Всего по группам	6132	11423	11201	9667	7226	35142	106830	393761
Общее									581382	100

Таблица 2 Объем (количество информации) отдельной транзакции (I, бит)

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
I	1060	1080	1070	1060	1080	1070	1010	1040	980	980	1170	1680	2560	2240	2080

№	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
I	2980	2720	1080	1010	1040	1030	1020	1080	1060	1060	1020	1040	1020	1020	1280

Решение задачи 1

Определить такое допустимое распределение транзакции Q={} по исполнителям, что удовлетворяется условие (1) и обеспечивает наиболее равномерную загрузку подразделений; т.е. минимизирует функцию  (2). Так как имеется 8 групп, то К = 8. 

Данная задача относится к задаче комбинаторного программирования [6,7,8,9,10].

А л г о р и т м  р е ш е н и я  с помощью ПО Excel:

1. Нахождение объема информации (потоков)

1.1.Нахождение величины потока в месяц. Умножим каждый столбец матрицы  (табл. 1) на матрицу  I (табл.2), в результате  получится матрица потоков информации по группам за месяц:

Табл. 3. Объем информации (поток) за 1 месяц .

№	Ректорат	Уч отдел	Метод Отдел	Науч отдел	Библио тека	Деканат	Препода ватели (10 факульт)	Студенты (10 тыс)
1	543780	1414040	433540	445200	232140	3032660	5168560	42671360
2	497880	1307880	333720	338040	0	2811240	5065200	34886160
3	409810	340260	304950	295320	0	2971390	4175140	40856880
4	556500	578760	2446480	2343660	0	2484640	8431240	40719900
5	345600	532440	2018520	1753920	0	2149200	7680960	38953440
6	388410	446190	2097200	2014810	0	2357210	7074840	36821910
7	1078680	440360	392890	414100	379760	571660	1013030	0
8	1147120	603200	422240	431600	405600	594880	1062880	0
9	490980	372400	304780	289100	245980	239120	0	0
10	476280	554680	323400	391020	277340	228340	0	0
11	0	427050	0	0	0	2178540	2417220	10893870
12	0	809760	0	0	0	2699760	6704880	21876960
13	0	2265600	0	0	0	5975040	6830080	0
14	0	1662080	0	0	0	7743680	7694400	0
15	0	1270880	0	0	0	4908800	0	0
16	0	1302260	0	0	0	8913180	10826340	0
17	0	0	913920	0	0	0	5467200	11100320
18	0	0	325080	0	0	0	1331640	0
19	0	0	300980	0	0	0	4117770	0
20	425360	1119040	0	0	0	2681120	3473600	31674240
21	0	0	0	579890	912580	0	0	3932540
22	0	0	426360	0	0	0	1591200	0
23	0	0	299160	0	0	0	4426920	0
24	0	0	593600	559680	1785040	0	13361300	15963600
25	0	0	461100	349800	1567740	0	13858440	19978880
26	0	0	0	0	577320	0	1332120	2282760
27	0	0	0	0	646880	0	0	0
28	0	0	0	0	479400	0	0	0
29	0	234600	0	0	0	682380	4776660	39786120
30	0	401920	0	0	0	1140480	7525120	49002240
Всего в гр.	6360400	16083400	12397920	10206140	7509780	54363320	135406740,00	441401180
Общее								683728880

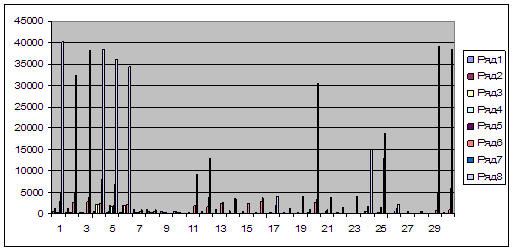
Рис. 1. Гистограмма распределения потоков по узлам за месяц

1.2. Нахождение потока в единицу времени (сек)

Обычно при настройке производительности учитывается загрузка потоков в единицу времени – 1 сек (бит/сек). Поэтому по данным о загрузке транзакции в месяц найдем загрузку сервера за 1 секунду. Так как 1 месяц = 864 000 сек. (60*60*8*30=864 000), это исходя из того, рабочий день равен 8 часам. Разделив каждый элемент матрицы  на 864 000, находим матрицу потоков информации по группам, поступающих за  секунду , в результате табл. 3 преобразуется в табл. 4:

Таблица 4. Объем информации (поток), поступающий за секунду

№	Ректорат	Уч отдел	Метод Отдел	Науч отдел	Библио тека	Деканат	Препода ватели (10 факульт)	Студенты (10 тыс)
1	0,629375	1,63662	0,501782	0,515278	0,268681	3,510023	5,98213	49,38815
2	0,57625	1,51375	0,38625	0,39125	0	3,25375	5,8625	40,3775
3	0,474317	0,393819	0,352951	0,341806	0	3,439109	4,832338	47,28806
4	0,644097	0,669861	2,831574	2,712569	0	2,875741	9,75838	47,12951
5	0,4	0,61625	2,33625	2,03	0	2,4875	8,89	45,085
6	0,449549	0,516424	2,427315	2,331956	0	2,728252	8,188472	42,61795
7	1,248472	0,509676	0,454734	0,479282	0,439537	0,661644	1,172488	0
8	1,327685	0,698148	0,488704	0,499537	0,469444	0,688519	1,230185	0
9	0,568264	0,431019	0,352755	0,334606	0,284699	0,276759	0	0
10	0,55125	0,641991	0,374306	0,452569	0,320995	0,264282	0	0
11	0	0,494271	0	0	0	2,521458	2,797708	12,60865
12	0	0,937222	0	0	0	3,124722	7,760278	25,32056
13	0	2,622222	0	0	0	6,915556	7,905185	0
14	0	1,923704	0	0	0	8,962593	8,905556	0
15	0	1,470926	0	0	0	5,681481	0	0
16	0	1,507245	0	0	0	10,31618	12,53049	0
17	0	0	1,057778	0	0	0	6,327778	12,84759
18	0	0	0,37625	0	0	0	1,54125	0
19	0	0	0,348356	0	0	0	4,765938	0
20	0,492315	1,295185	0	0	0	3,103148	4,02037	36,66
21	0	0	0	0,671169	1,056227	0	0	4,551551
22	0	0	0,493472	0	0	0	1,841667	0
23	0	0	0,34625	0	0	0	5,12375	0
24	0	0	0,687037	0,647778	2,066019	0	15,46447	18,47639
25	0	0	0,533681	0,404861	1,814514	0	16,03986	23,1237
26	0	0	0	0	0,668194	0	1,541806	2,642083
27	0	0	0	0	0,748704	0	0	0
28	0	0	0	0	0,554861	0	0	0
29	0	0,271528	0	0	0	0,789792	5,528542	46,04875
30	0	0,465185	0	0	0	1,32	8,70963	56,71556
Всего в группе	7,361574	18,61505	14,34944	11,81266	8,691875	62,92051	156,7208	510,881
Общее								791,3529

2. Поиск выражения, удовлетворяющего условию (1)

2.1. Расчет выражения (1) без условия

Данная задача комбинаторная, поэтому для каждой операции необходимо провести всевозможные комбинации выборок. Для нашего случая 1073741824 комбинации. Число ячеек в Excel не достигает такого большого размера, поэтому из 30 транзакции выберем 12 самые часто встречающие транзакции (табл. 5). Эти транзакции входят в один бизнес-процесс, который будет рассмотрен ниже. Таким образом,  комбинации.  Число строк комбинаторной матрицы К (табл. 6) составляет 4096, а число столбцов - 12.

Таблица 5. Выбор 12 транзакции (поток информации за секунду) (E12)

0,644097	1,248472	1,327685	0,568264	0,55125	0	0,492315	0	0	0,492315	0	0
0,669861	0,509676	0,698148	0,431019	0,641991	0	0	1,295185	0	0	0,271528	0,465185
2,831574	0,454734	0,488704	0,352755	0,374306	0,37625	0,348356	0	0,493472	0,34625	0	0
2,712569	0,479282	0,499537	0,334606	0,452569	0	0	0	0	0	0	0
0	0,439537	0,469444	0,284699	0,320995	0	0	0	0	0	0	0
2,875741	0,661644	0,688519	0,276759	0,264282	0	0	3,103148	0	0	0,789792	1,32
9,75838	1,172488	1,230185	0	0	1,54125	4,765938	4,02037	1,841667	5,12375	5,528542	8,70963
47,12951	0	0	0	0	0	0	366,5998	0	0	46,04875	56,71556

Таблица 6. Фрагмент комбинаторной матрицы (K)

0	0	0	0	0	0	0	0	0	0	0	1
0	0	0	0	0	0	0	0	0	0	1	0
0	0	0	0	0	0	0	0	0	0	1	1
0	0	0	0	0	0	0	0	0	1	0	0
0	0	0	0	0	0	0	0	0	1	0	1
0	0	0	0	0	0	0	0	0	1	1	0
0	0	0	0	0	0	0	0	0	1	1	1
0	0	0	0	0	0	0	0	1	0	0	0

Для вычисления выражения (1) выполним произведение элементов каждого столбца (8 групп) матрицы E12 на каждый столбец матрицы K, используя формулу ЛИСТ2!$J$1*ЛИСТ5!J1 + ЛИСТ2!$J$2*ЛИСТ5!J2 + ЛИСТ2!$J$3*ЛИСТ5!J3 + ЛИСТ2!$J$4*ЛИСТ5!J4 +  ЛИСТ2!$J$5*ЛИСТ5!J5 +  ЛИСТ2!$J$6*ЛИСТ5!J6 + ЛИСТ2!$J$7*ЛИСТ5!J7 + ЛИСТ2!$J$8*ЛИСТ5!J8 + ЛИСТ2!$J$9*ЛИСТ5!J9 + ЛИСТ2!$J$10*ЛИСТ5!J10 + +ЛИСТ2!$J$11*ЛИСТ5!J11 + ЛИСТ2!$J$12*ЛИСТ5!J12. Получим матрицу , просуммировав ее каждый столбец матрицы, то есть все числа из диапазона ЛИСТ6!A1: A4096 (всевозможные комбинации - 4096), получим матрицу :

Таблица 7. Распределение потоков (равномерная нагрузка) без ограничений (бит в сек) ()

	Ректорат	Уч отдел	Метод Отдел	Науч отдел	Библио Тека	Деканат	Препо даватели (10 факуль тетов)	Студенты
Транзак Ции	10904,37	10204,35	12423,99	3102,056	3102,056	20438,8	78159,17	1057778,96
Сумма	1196114

2.2 Расчет с учетом условия (ограничения на поток)

Действующая загрузка сервера рассчитана на 1 Мбит/сек. Вводя данное ограничение С =1 000 000 для полученного значения находим поток для каждой группы пользователей, используя формулу =ЕСЛИ(СУММ(Лист6!A1:A4096)<= Лист7!E4099; Лист7!A1:A4096).  Для понятности в формуле записан весь диапазон (выделено красным цветом), в самом деле записывается одна ячейка для результата, а потом с помощью мыши перетаскивается по всему диапазону (столбцу). Результат дан в табл. 8:

Таблица 8. Оптимальное распределение потоков по группам пользователей (бит в сек) ()

	Ректорат	Уч отдел	Метод Отдел	Науч отдел	Библио Тека	Деканат	Препо даватели (10 факуль тетов)	Студенты
Транзак ции	10904,37	10204,35	12423,99	3102,056	3102,056	20438,8	78159,17	999841, 6475
Сумма	1138176

3. Оптимизация распределения потоков.

Вычислив формулу (2), получим Ф= 105584481878,27 (ячейка Лист7!D4100). Таким образом, допустимое распределение транзакции по всем исполнителям, то есть 8 равна 105584481878,27.  Выражение (2) выражает дисперсию генеральной совокупности (в нашем случае - 12 чисел) и также определяется формулой ДИСПР() в Excel. Это окончательный итог задачи 1.

Постановка задачи 2.

Еще одним критерием распределения операции по рабочим местам является обеспечение требуемой скорости обработки информации с учетом функциональных или технологических связей между операциями. Если в каждой группе   транзакции, относящиеся к одному и тому же бизнес-процессу будут обрабатываться не дольше чем 60 минут в месяц (60*30=1800 сек); то общее время на обработку будет сК и вся система будет работать в сбалансированном режиме. Пусть время на обработку одной транзакции , а затраты на сокращение этой длительности на величину  составляет ). Тогда  задача состоит в отыскании такого разбиения транзакции по группам и величин , которое бы обеспечивало требуемый такт c  с минимальными затратами.

Как описано в [6,7] -все транзакции относятся к тем или иным бизнес-процессам, которые в свою очередь можно представить в виде графа, вершины которого соответствуют операциям, а дуги - последовательности выполнения. Другими словами, приступить к обработке очередной транзакции после того, как завершена предшествующая. Как и раньше, будем обозначать Q={}  - распределение транзакции по группам , удовлетворящим требуемой последовательности операции.

Определить допустимое распределение транзакции по группам Q={}  и  величины , сокращения продолжительности операции минимизирующее (3) при ограничениях i=1,…N  (4)  k=1,...K.

Данные

Табл. 9. Время обработки и длительности сокращений транзакции (T , TAU)

N	4	7	8	9	10	18	19	20	22	23	29	30
T	8	8	8	10	10	8	8	8	8	8	10	10
TAU	2	2	2	3	3	2	2	2	2	2	3	3

В первой задаче были определены потоки информации из 12 часто встречающимся транзакции, не учитывая сами бизнес-процессы. Вторая задача посвящается определению скорости обработки транзакции, входящих к конкретному бизнес-процессу. Приведем самые большие по загруженности бизнес-процессы, это “Студент” и “Преподаватель” (табл. 10 и 11). Заметим, что в процессе “Преподаватель” задействованы 11 транзакции только в 6 группах. А в процессе “Студент” задействованы 8 транзакции только в 4 группах.

Пользователь	Номера транзакции
Ректорат	4,7,20,8→                                    →9,10
Уч. отдел	→7,20,8→                        →9,10→
Метод. Отдел
Науч. отдел
Библиотека
Деканат	→7,8,20→                →9,10→
Преподаватели	→20,29,30→
Студенты

Пользователь	Номера транзакции
Ректорат	4,7,8→                                          →9,10
Уч. отдел	→7,8→                              →9,10→
Метод. Отдел	→7,8,18,19→
Науч. отдел	→7,8,22,23→
Библиотека
Деканат	→7,8→               →9,10→
Преподаватели	→29,30→
Студенты

Таблица 10. Бизнес-процесс “Преподаватель   Таблица 11. Бизнес-процесс “Студент”

Решение задачи 2

Как известно из первой задачи, мы выбрали 12 наиболее встречающиеся транзакции. Их время выполнения и затраты на сокращение выполнения даны в табл. 9. Решим конкретную задачу для первого случая, то есть для бизнес - процесса “ Преподаватель ”.

А л г о р и т м  р е ш е н и я:

1. Нахождение времени обработки

Нахождение времени, необходимое на обработку транзакции в бизнес-процессе “Студент”, для этого определим матрицу из данных из T (табл. 9, строка 2):

Таблица  12. Время обработки операции бизнес - процесса “ Преподаватель ” ().

8	8	8	10	10	0	0	0	0	0	0	0
0	8	8	10	10	0	0	0	0	0	0	0
0	8	10	0	0	8	8	0	0	0	0	0
0	8	8	0	0	0	0	0	8	8	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	8	8	10	10	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	10	10
0	0	0	0	0	0	0	0	0	0	0	0

Далее выполним произведение каждого столбца матрицы  (табл. 12) на каждый столбец комбинаторной матрицы K (табл. 6.) и находим матрицу общей продолжительности выполнения для одной группы  (запишем результаты в Лист8!A1: A4096 по Лист8!H1: H4096) и просуммируем все комбинации для групп,  участвующих в процессе, используя формулу =СУММ(Лист8!A4097: H4097), тогда для каждой группы имеем:

Таблица 13. Время выполнения операции по группам ()

№	Ректорат	Уч. отдел	Метод. отдел	Науч. отдел	Деканат	Преподаватель
Время обработки	90112	73728	69632	65636	73728	40960
Сумма	413696

2.Нахождение времени сокращении. Аналогично найдем время сокращений затрат:

Таблица 14. Время сокращения операции по группам ()

№	Ректорат	Уч. отдел	Метод. отдел	Науч. отдел	Деканат	Преподаватель
Время обработки	24576	20480	24576	16384	20480	12288
Сумма	118784

Запишем результат в Лист9!A4097: H4097.

3.  Поиск выражения, удовлетворяющего условию (4);

Находим максимум времени сокращений для одной группы, то есть матрицу и запишем в ячейку Лист9!H4100. Он равен 12. Далее просуммируем разности времени обработки и сокращений затрат (матрица V12), результат запишем в Лист10!A1: A4096 по Лист10!H1: H4096. Введем ограничение, то есть оценку сверху – S=1800 сек. по формуле =ЕСЛИ(СУММ(Лист9!A1: $H$4096)<= Лист10!E4099; Лист10!A4097: H4097), и просуммируем по всем комбинациям (матрица ) по формуле СУММ(Лист10!A4097: H4097), найдем решение задачи.

Таблица 15. Фрагмент матрицы ограничений (Z12)

ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	14
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	24	ЛОЖЬ	14
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	12	ЛОЖЬ	0
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	12	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	12	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	12	ЛОЖЬ	14
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	18	ЛОЖЬ	0
ЛОЖЬ	ЛОЖЬ	18	18	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	18	18	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	18	18	ЛОЖЬ	14
ЛОЖЬ	ЛОЖЬ	18	18	ЛОЖЬ	0
ЛОЖЬ	ЛОЖЬ	18	18	ЛОЖЬ	7
ЛОЖЬ	ЛОЖЬ	18	18	ЛОЖЬ	7

Таблица 16. Оптимальное время выполнения по группам (SKOR)

№	Ректорат	Уч. отдел	Метод. отдел	Науч.отдел	Деканат	Преподаватели
Оптимальное время	1772	1778	1800	1784	1800	1798
Среднее	1788,667

Результат (матрица SKOR) запишем  в диапазон ячеек Лист10!A4097: H4097. Это окончательный итог задачи 2. Среднее значение будет равно 1788,667.

Заключение: Администраторам серверов и баз данных наверняка приходится настраивать систему на быструю и эффективную обработку посылаемых приложениями запросов. Выполнить настройку производительности на уровне сервера [4,15,16,17,18] можно различными способами: улучшением организации ввода/вывода данных на диски, увеличением памяти или созданием и модификацией индексов.

При проектировании корпоративной информационной системы учитываются требования к 3 основным параметрам [4,6,11,12]:

- пропускная способность;

- надежность;

- стоимость.

Рассмотреная модель позволяет выполнять анализ производительности системы по первому и второму параметру, например:

1) варьируя значение максимального потока (в данном приемере с=1000 000 Бит/сек) можно определять пропускную способность системы (распределение потоков) для конкретной группы пользователей;

2) варьируя значение максимального времени задержки (в данном приемере с=1800 сек в месяц) для конкретной группы пользователей, можно определять надежность системы.

Учитывая введенное ограничение на задержку для группы (оно составляет 1800/413696=0,004351-ю долю от общего времени обработки), что надежность системы обеспечивается достаточно хорошо.

Таким образом, результаты исследования рассмотренной работы можно использовать при настройке производительности корпоративной информационной системы, в частности, для определения допустимой загрузки потоков по группам пользователей и оптимизации времени обработки.

  Литература

1. Концепция стратегического развития Республики Казахстан «Казахстан – 2030». – Астана, 1998.

2. Государственная программа развития образования в Республике Казахстан на 2005–2010 гг. Утверждена указом президента Республики Казахстан от 11 октября 2004 года №1459.

3. Стратегический план развития Международного Казахско-турецкого университтета им. А. Ясауи на 2009-2013 г. Туркестан, 2010.

4. Oracle. Application implementation method consulting handbook. Oracle corporation, 1994.

5. Новиков Д. А., Цветков А. В., Гламаздин Е. С. Управление корпоративными программами: информационные системы и математическое модели. -М.: Компания Спутник, 2003.-159 с.

6. С. В. Сочнев, Г. С. Хулап. Технологии и системы информационного корпоративного управления. 2002. -200 с.

7. Сочнев С В. Критерии выбора контрольных точек радиоэлектронной аппаратуры для оценки ее работоспособности. Техника средств связи. Выпуск 4, М. 1988.

8. Бурков В. Н, Новиков Д. А., Заложнев А. Ю. Теория графов в управлении организационными системами. М.: Синтег, 2001.

9. Лифшиц А. Л., Мальц Э. А.   Статистическое моделирование систем массового обслуживания// -М.: Сов. Радио, 1978, -248 с.

10. Гмурман в. Е. Руководство к решению задач по теории вероятности и математической статистики// -М.:Высшая школа, 1975.

11. Тукубаев З. Б. и др. Моделирование и исследование алгоритмов распределения нестационарных приоритетных потоков в сети СМО// Сб.“Алгоритмы” АН РУ, Ташкент, вып. 60, 1986.

12. Тукубаев З. Б. и др. Модель эффективной загрузки узлов сети//. Тезисы докладов XI – всесоюзного совещания по проблемам управления, г.Ташкент, 1989.

13. Тукубаев З. Б. Обобщенные модели в системах массового обслуживания//. “Вестник МКТУ”, №2, г. Туркестан, 2006.

14. Тукубаев З. Б., Умаров А. А. Автоматизация деятельности вуза - задача Правительства Республики Казахстан. Журнал “Актуальные проблемы гуманитарных и естественных наук”, М. 2010.

15. Умаров А. А. Проектирование базы данных методом нормализации. www.citforum.ru. 2008.

16. Умаров А. А., и др. Разработка веб-узла фирмы “Абба”. V всероссийская школа-семинар молодых ученых “Управление большими системами”. Сб. Трудов.-Т.2, Липецк, 2008.

17. Тукубаев З. Б., Умаров А. А. Моделирование и исследование алгоритмов динамического управления потоками сообщений в информационно-вычислительных сетях. X-я международная научно-техническая конференция «Кибернетика и высокие технологии XXI века» . Воронеж. 2009.

18. Тукубаев З. Б., Умаров А. А. Анализ потоков сообщений, поступающих на веб-сервер организации // Сб. науных трудов “Вестник МКТУ”, №3, с.42-45, г. Туркестан, 2009