BC/NW 2010; №2 (17):11.3

МЕТОД ПОСТРОЕНИЯ ЦИФРОВОЙ СИСТЕМЫ ЗАЩИЩЕННОЙ ПЕРЕДАЧИ РЕЧЕВОЙ ИНФОРМАЦИИ

Савватин А.И., Новоселов С.А.

(Ярославский государственный университет им. П.Г. Демидова, Россия)

Введение

На данный момент необходимо решать задачи защиты информации в каналах связи наиболее простыми и быстрыми методами. Это касается как сетей передачи данных с коммутацией каналов, так и с пакетной коммутацией. Большинство существующих алгоритмов основаны на математических методах и имеют сложную структуру, не позволяющую реализовать эти алгоритмы защиты на простой элементной базе.

Вейвлет-анализ является перспективным направлением цифровой обработки сигналов, его инструменты находят применение в самых различных сферах интеллектуальной деятельности. В данной работе предлагается использование цифровых вейвлет-фильтров для построения систем защищенной передачи речевой информации. Рассмотрены некоторые теоретические аспекты согласованного вейвлет-преобразования, а также показана возможность применения данного аппарата в задаче защиты речевой информации. Под защитой передачи речевой информации может пониматься как сокрытие самого факта передачи информации по каналам связи, так и передача речевого сигнала по каналам в зашифрованном виде.

На сегодняшний день существует несколько известных методов защиты передачи цифровой информации: наложение защитного шума, временные и частотные преобразования, использование динамического хаоса, криптографические методы. Наряду с методами цифровой обработки применяются аналоговые методы. Как правило, в сигнале, закрытом с помощью аналоговых методов, все-таки сохраняются отдельные признаки открытого речевого сообщения. В целом аналоговые методы защиты информации обеспечивают меньшую степень закрытия речевых сигналов по сравнению с цифровыми [1].

Почему вейвлеты?

Вейвлет-анализ – это исследование сигнала при помощи базисных функций. Применяемые для этой цели базисы были названы вейвлетами – функциями двух аргументов – масштаба и сдвига: . В отличие от традиционного преобразования Фурье, вейвлет-преобразование обеспечивает двумерное представление исследуемого сигнала в области масштаб-положение. Аналогом частоты при этом является масштаб аргумента базисной функции, а положение характеризуется её сдвигом . Это позволяет разделять крупные и мелкие особенности сигналов, одновременно локализуя их на временной шкале. Иными словами, вейвлет-анализ можно охарактеризовать как спектральный анализ локальных возмущений [2, 3].

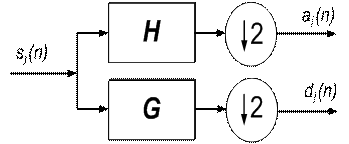
Идея дискретного вейвлет-анализа состоит в представлении сигнала последовательностью образов с разной степенью детализации (кратномасштабный анализ), что позволяет выявить локальные особенности сигнала и классифицировать их по интенсивности. Как показано на схеме (рис. 1), дискретное вейвлет-преобразование (ДВП) осуществляется с использованием цифровых вейвлет-фильтров , и блоков децимации.

Рис.1. Одноуровневое вейвлет-разложение

Таким образом, кратномасштабный вейвлет-анализ сводится к нахождению коэффициентов аппроксимации и детализирующих коэффициентов в разложении сигнала .

Ниже описано, как благодаря уникальным свойствам согласованных вейвлет-фильтров (СВФ) и ортогональному ДВП, можно выделять полезный сигнал и помеху из их аддитивной смеси. Для реализации ортогонального ДВП необходимо, чтобы АЧХ вейвлет-фильтра удовлетворяла следующим условиям:

1. Положительность АЧХ .

2. Ортогональность .

3. Наличие нулевых моментов ЧХ .

Далее опишем, как выполнить расчет вейвлет-фильтра (ВФ), который обеспечивает полное восстановление сигнала после процедуры одноуровневого вейвлет-разложения, используя только низкочастотные компоненты разложения.

Построение согласованных вейвлет-фильтров

Теорию СВФ можно развить из следующей задачи. Пусть имеется некоторая функция . Требуется построить для неё набор ортогональных квадратурно-зеркальных вейвлет-фильтров таким образом, чтобы при разложении (здесь – Фурье образ сигнала , – оператор обратного преобразования Фурье) на вейвлет-коэффициенты на выходе детализирующего фильтра был ноль, т.е. все детализирующие коэффициенты должны быть равны нулю. Оказалось, что данная задача может быть с успехом решена.

Процедура вейвлет-преобразования сигнала в частотной области будет выглядеть следующим образом:

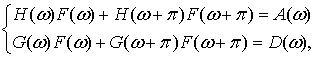(1)

где , – Фурье образы аппроксимирующих и детализирующих коэффициентов вейвлет-преобразования соответственно, а и – частотные характеристики (ЧХ) низкочастотного и высокочастотного фильтров разложения. Учитывая требование наличия как минимум одного нулевого момента ЧХ фильтра , определим . Можно принять, что между фильтрами и установлено соотношение [4]

(2)

Это позволит сразу удовлетворить одно из ограничений, накладываемых на фильтры:

где , - ЧХ соответствующих фильтров восстановления, причем и .

Еще одно важное свойство – свойство ортогональности вейвлет-базиса для фильтров в частотной области, которое записывается в виде

(3)

Решим систему (1) в предположении, что , используя соотношение (2). Получим

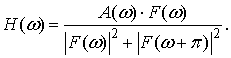(4)

Фильтр почти построен, осталось только найти условие на . Это можно сделать с помощью (3), учитывая, что В результате чего имеем

Пусть - действительная функция, тогда .

Окончательный результат представим в виде

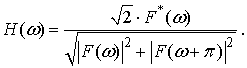(5)

Для проверки того, насколько сильно СВФ повторяют сигнал, который использовался для синтеза фильтров, произведен синтез СВФ для известных ранее вейвлетов (они использовались в качестве исходного сигнала). Выяснилось, что данный метод «ортогонализирует» исходный сигнал, создавая новый вейвлет-базис. Для численной проверки алгоритма синтеза предложено построить фильтры для вейвлетов Добеши. Как и следовало ожидать, получены соответствующие фильтры Добеши [5].

В результате решения задачи найдены цифровые вейвлет-фильтры, согласованные с последовательностью . Согласованные вейвлет-фильтры «обеспечивают предсказание» детализирующих коэффициентов вейвлет-разложения по аппроксимирующим коэффициентам для сигнала, с которым они согласованы. Полное восстановление этого сигнала происходит только по аппроксимирующим коэффициентам [6].

Особенность данных фильтров состоит в том, что их импульсная характеристика формируется с учетом характеристик обрабатываемого сигнала. В нашем случае – это ключевая последовательность. Таким образом, информация о сигнале закладывается в сам фильтр. Это свойство используется для построения защищенной схемы передачи цифровой информации. Необходимо построить банк вейвлет-фильтров, согласованный с «защитной» ключевой последовательностью , и применить следующую схему передачи информации (рис. 2).

Алгоритм защиты передачи информации

Возьмем инверсную схему одноуровневого вейвлет-преобразования. Фильтры можно построить с использованием известных вейвлетов Добеши, Хаара, но это не обеспечит надежной защиты информации. Требуются уникальные квадратурно-зеркальные ортогональные вейвлет-фильтры, характеристики которых зависят от единственной ключевой последовательности.

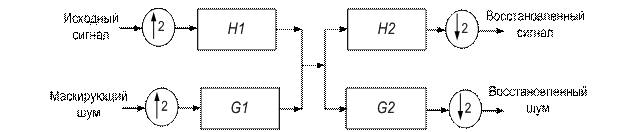
Для защиты передачи информации используется свойство уникальности фильтров восстановления (Н2, G2) для фильтров разложения вейвлет-преобразования (Н1, G1) [7]. На приемном конце должен быть известен уникальный ключ, с помощью которого зашифрована информация на передающей стороне.

Рис. 2. Блок-схема алгоритма

Физически процесс формирования защищенного сигнала можно объяснить следующим образом: полезный сигнал после прохождения через фильтр Н1 представляет собой сумму взвешанных аппроксимирующих функций, где коэффициенты взвешивания есть отсчеты сигнала в определенные моменты времени. Маскирующий шум на выходе фильтра G1 является суммой взвешанных вейвлет-функций, где коэффициенты взвешивания есть отсчеты белого гауссовского шума (БГШ). Аддитивную смесь такой помехи и полезного сигнала легко разделить, основываясь на ортогональности аппроксимирующей и вейвлет-функций. Выбор ключа изначально определяет форму этих функций.

Исследования и выводы

Алгоритм реализован в среде программирования MatLab. Исследования проводились на речевых сигналах. К системе предъявлялись следующие требования качества закрытия речи:

1. Обеспечение разборчивости речи и узнаваемость говорящего.

2. Высокая степень защиты информации. Сигнал в канале по свойствам напоминает БГШ. Выделить полезный сигнал из смеси можно, зная уникальную импульсную характеристику фильтра восстановления H2, которая определяется ключом.

3. Достаточное число ключевых комбинаций и простота их генерации. Исследованная система эффективна для любого размера ключа. Но следует отметить, что при малой длине ключа (порядка десяти отсчётов) незначительное изменение ключевой последовательности на приемной стороне приводит к невозможности восстановления передаваемой информации. Это определяет уникальность ключа и является положительным фактором для защиты информации. Функциональность системы также зависит от соответствия длин ключевых последовательностей на передающей и приемной стороне, при несоответствии длин информацию не восстановить. Установлено, что неэффективно использовать очень длинные ключи, так как уменьшается быстродействие алгоритма в результате длительных сверток.

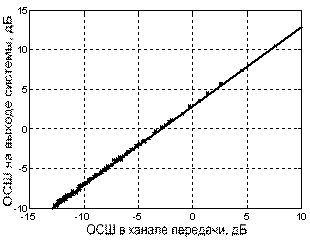
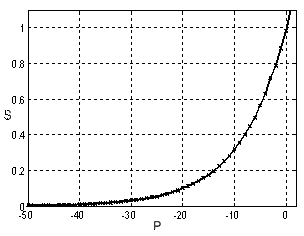
Рис. 3. Соотношение ОСШ в системе для полезного сигнала	Рис. 4. Зависимость СКО сигнала (S) от мощности внешнего шума в канале (P)

4. Помехозащищенность системы. Система устойчива к внешним шумам: ОСШ на выходе системы больше, чем ОСШ в канале на 3 дБ, причем зависимость ОСШ на выходе системы от ОСШ в канале линейна (рис. 3). Следовательно, такая система защиты информации помехоустойчива. Зависимость среднеквадратичного отклонения сигнала на выходе системы от мощности внешнего шума в канале (рис. 4) имеет экспоненциальную зависимость. При увеличении мощности внешнего шума искажение полезного сигнала становится все более заметным.

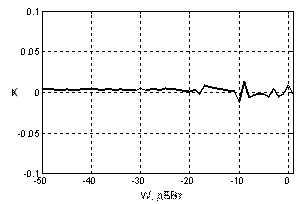
5. Отсутствие корреляции входного сигнала и сигнала в канале. Коэффициент корреляции близок к нулю, что также является положительным фактом для закрытия информации (рис. 5).

Рис. 5. Зависимость коэффициента кореляции (K) от мощности маскирующего шума (W)

6. Простота реализации и быстродействие. В алгоритме применяется только свертка сигналов с импульсной характеристикой фильтров, децимация и интерполяция. Быстрые алгоритмы цифровой обработки сигналов позволяют обрабатывать сигнал в реальном времени.

Заключение

В работе предложен алгоритм защиты речевой информации с использованием инверсной схемы одноуровневого вейвлет-преобразования. Для построения системы существенным являлась уникальность ВФ, согласованных с ключом, и свойство ортогональности квадратурно-зеркальных ВФ. Для построения СВФ использовалась формула (5), которая теоретически обоснована и практически исследована.

Проведена оценка криптостойкости алгоритма. Уникальность ключа для канала передачи информации позволяет говорить об уникальности банка вейвлет-фильтров, использующегося в системе. Общеизвестные вейвлет-фильтры Добеши не позволяют расшифровать сигнал, если он зашифрован с помощью фильтров H1, G1, построенных на основе использования некоторого ключа на передающей стороне. Для шифрования целесообразно использовать БГШ по мощности превышающей уровень мощности полезного сигнала.

Стоит отметить, достоинством алгоритма является скрытие факта передачи информации в работающем канале. Некоторым недостатком алгоритма является то, что для сохранения качества речевой информации нужно увеличить скорость передачи в канале в 2 раза. Но это не так критично для современных систем. Метод не требует синхронизации, устойчив к временным задержкам.

Использование многоуровневого вейвлет-преобразования открывает новые возможности защиты информации, но усложняет алгоритм. Данное направление требует отдельного исследования.

Перспективным является использование алгоритма для защиты от «прослушивания» VoIP трафика в сети Интернет, телефонных переговоров сетей ISDN, маскирования радиосвязи. Алгоритм эффективен для защищенной передачи и других типов данных, что может найти применение при видеоконференцсвязи, передаче мультимедийной информации.

ЛИТЕРАТУРА

1. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. М.:Триумф, 2002.

2. Малла С. Вейвлеты в обработке сигналов. М.:Мир, 2005.

3. Чуи Ч. Введение в вейвлеты. М.:Мир, 2001.

4. Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. ВУС, 1999.

5. Daubechies I. Ten Lectures on Wavelets. SIAM, Philadelphia, PA, 1992.

6. Новоселов С.А. Применение согласованных одномерных вейвлет-фильтров в задаче распознавания речевых сигналов // Докл. 9-й междунар. конф. «Цифровая обработка сигналов и ее применение». М., 2007. Т.1 С.146-149.

7. Новоселов С.А., Савватин А.И. Использование согласованных вейвлет-фильтров в задаче защиты речевой информации // Докл. 12-й междунар. конф. «Цифровая обработка сигналов и ее применение». М., 2010. Т.2. С.209-211.