BC/NW 2010; №2 (17):12.2

ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ КОМПЬЮТЕРНОГО ОБУЧЕНИЯ ПРИ ОСВОЕНИИ ПРОСТЫХ И СЛОЖНЫХ НАВЫКОВ

Лебедев Г.Н., By С.Д.

(Московский авиационный институт (государственный технический университет), Россия)

Введение

Как показал опыт компьютерного обучения, имеет смысл индивидуализировать распределение времени на освоение навыков с учетом способности каждого обучаемого и сложности самих навыков. Эта способность, прежде всего, зависит от качества обучения или «успеваемости» на предыдущих этапах и от степени деградации умения со временем (способности помнить или забывать усвоенное).

Поэтому необходимо изучить эти способности, что означает сформировать математическую модель качества обучения и далее оценить параметры этой модели для каждой индивидуальной группы, для чего предлагается решение обратной задачи оптимизации. Полученные оценки позволят поставить и решить прямую задачу оптимального гибкого планирования обучения, что должно обеспечить положительный эффект, а ее реализация возможна в компьютерном классе.

В зависимости от результатов оптимизатор плана назначает новый тип задания, в том числе время его освоения каждым учеником с учетом заданного общего времени на обучение. Целью данной работы является раскрыть механизм идентификации и последующей оптимизации в расчете на индивидуальное обучение.

Выбор математической модели оценки качества освоения навыков и анализ особенностей оптимизации обучения.

Учтем наиболее важные факторы, влияющие на освоение одного навыка:

• скорость освоения навыков;

• уровень освоения предшествующих навыков, на которых базируется рассматриваемый;

• степень деградации или «забывания» предшествующих навыков к моменту освоения нового.

Для простых навыков наиболее приемлемой освоения навыка моделью является экспоненциальная зависимость вида (рис. 1):

; , (1)

где - нормированная оценка качества обучения, когда максимальный уровень освоения принят за единицу, - отведенное время на обучение, - персональный показатель скорости освоения простого навыка, подлежащий идентификации, - показатель степени, меняющийся в зависимости от индивидуальных особенностей обучаемого.

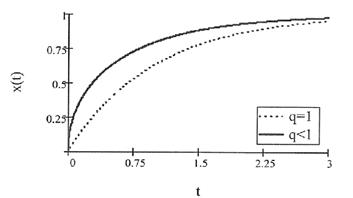
Рис. 1. График функции экспоненциальной зависимости

Из рис. 1 видно, что скорость освоения вначале велика (чем меньше , тем она больше), а потом по мере обучения она падает, и дальнейшая трата времени становится неэффективной.

Для сложного навыка характерны низкая скорость освоения вначале, максимальная скорость в середине и убывание скорости при подходе к максимальному уровню, как показано на рис. 2.

Логистический характер для сложного навыка может быть представлен формулой [2]:

; , (2)

где - нормированная оценка качества обучения, – отведенное время на обучение, - персональный показатель скорости освоения сложного навыка, подлежащий идентификации, - персональный показатель степени, увеличение которого подчеркивает логистический характер обучения.

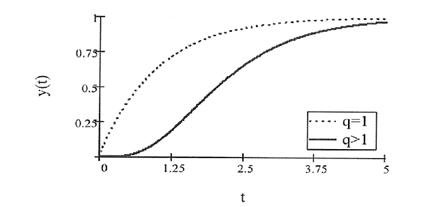
Рис. 2. График функции логистической зависимости

При параллельном освоении простых и сложных навыков суммарное время на очередном этапе обучения ограничено, поэтому при оптимизации приходится жертвовать одними навыками в угоду другим, а это в значительной степени зависит от индивидуальных особенностей обучаемого и требует знания параметров критерия , которые нужно предварительно определить.

Постановка задачи идентификации

Рассмотрим задачу многоэтапного освоения навыков при их параллельном изучении на каждом этапе при следующих допущениях.

· Задано общее число этапов обучения и общее число параллельно осваиваемых навыков, одинаковое на каждом этапе: простых и сложных навыков.

· Качество освоения простого навыка растет по экспоненциальной модели (1), качество сложного навыка - по логистической модели (2), параметры которых подлежат идентификации по результатам тестирования на очередном этапе обучения.

· Показатели скорости обучения и в свою очередь линейно зависят от результатов обучения на предыдущем этапе (ν - 1):

, (3)

где или - скорости освоения простого или сложного навыка в «отсутствии» обучения на предыдущих этапах, назначаемые экспертом-преподавателем априорно, и - искомые коэффициенты корреляции новых навыков с предыдущими; и - средняя успеваемость при интегральной оценке освоения соответственно простых и сложных навыков на предыдущем этапе.

· Контингент обучаемых делится на три группы: сильные , средние и слабые , которые получают соответствующие оценки и при тестировании на каждом этапе обучения.

· В общем виде критерий оптимальности обучения представлен формулой

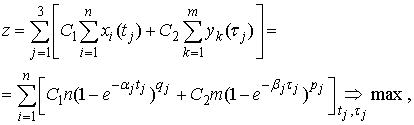(4)

если за оптимум принять максимальную суммарную (или среднюю) успеваемость всего контингента при учете линейных ограничений:

, (5)

, . (6)

При этих допущениях требуется:

§ провести оценку параметров скорости освоения простых и сложных навыков и коэффициентов взаимосвязи и по результатам тестирования;

§ осуществить оптимальное планирование индивидуального обучения на новом этапе для каждой из трех учебных групп [3, 4].

Идентификация параметров критерия по результатам тестирования и имеющимся учебным планам

Проведем необходимую оценку параметров при решении обратной задачи параметрической оптимизации в следующем виде - по данным тестирования определим показатели скорости освоения навыков на каждом этапе обучения.

Результаты тестирования по имеющимся учебным планам представлены в табл. 1, 2 (в табл. 1 для первого этапа и табл. 2 для второго этапа).

Таблица 1. Данные тестирования и результаты идентификации на этапе при ч

№ п/п	Имя
1		76	4,1	3,8	1,2	0,8	0,7	0,2	0,022	0,016	0,008
2		72	3,9	3,2	0,8
3		40	4,99	4,2	2,6	0,997	0,8	0,5	0,117	0,042	0,018
4		36	4,98	3,8	2,4
5		40	4,99	4,2	2,6
б		36	4,98	3,8	2,4

Таблица 2. Данные тестирования и результаты идентификации на этапе

№ п/п	имя
1		80	4,4	3,9	1,3	0,84	0,74	0,22	0,024	0,017	0,008
2		76	4	3,5	0,9
3		38	4,92	4	2,45	0,98	0,76	0,47	0,076	0,039	0,018
4		34	4,88	3,6	2,25
5		38	4,92	4	2,45
6		34	4,88	3,6	2,25

В этих таблицах после строки-заголовка две верхние строки соответствуют сложным навыкам, четыре нижних - простым. Третий столбец соответствует плановому распределению в часах времен и рассчитанных на «средние» способности обучаемых при заданном общем времени обучения - 300 ч. В столбцах 4-6 даны оценки качества обучения в пятибалльной системе, в столбцах 7-9 - им соответствующие пересчитанные нормированные оценки и .

Сначала найдем степени и . Их можно вычислить с помощью формул (1) и (2), пользуясь их обратимостью. В частности, рассмотрим обучение слабой группы сложному навыку в двух вариантах: при времени обучения и времени . Например, в качестве = 74 ч было взято значение из первого этапа обучения, а = 78 ч взято из второго этапа. Тогда согласно формуле (2) можно дважды записать

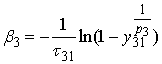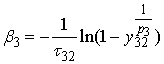; . (7)

Для слабой группы нормированные оценки и малы. Поэтому, приравнивая друг другу выражения для , получаем приближенную оценку:

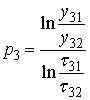. (8)

При перечисленных конкретных значениях , ,, значение

Аналогичным образом можно определять и другие значения и , но точность приближения при этом падает, что указывает на необходимость привлечения большего числа данных тестирования.

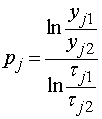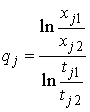; . (9)

В результате использования данных табл. 1 и 2 и формул (9) получили значения

При определении значений и при известных параметрах и можно воспользоваться обратимостью формул (1) и (2):

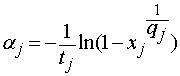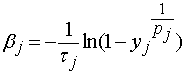; . (10)

Результаты вычислений показателей и при известных степенях представлены в столбцах 10-12 табл. 1 и 2. Они указывают, во-первых, на незначительное различие этих показателей на разных этапах обучения, во-вторых, чем сильнее группа, тем выше скорость обучения, т.е. и и, в-третьих, скорость освоения сложного навыка в любой группе ниже, чем простого, т.е. .

При оценке взаимосвязи между этапами обучения по формулам (3) необходимо предварительно решить вопрос назначения скоростей и , когда приходится «наверстывать упущенное». В этом гипотетическом случае можно рассуждать так.

Если обучение на этапе не было, то для слабой и средней групп дальнейшее освоение сложного навыка невозможно, т.е. , и лишь сильная группа, потеряв дополнительное время предыдущего этапа, может ликвидировать отставание. Поэтому примем оценку

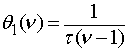. (11)

При обучении простым навыкам в отсутствии этапа невозможно обучение лишь для слабой группы, т.е. , а для средней и сильной групп допустимы оценки

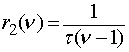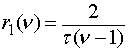; . (12)

Теперь с помощью формул (3), (11), (12) и найденных и , представленных в табл. 2, можно определить коэффициенты корреляции и , если воспользоваться из табл. 1 результатом обучения и на предшествующем этапе:

; ;

;

; ;

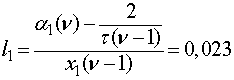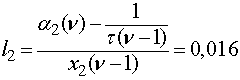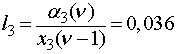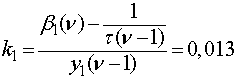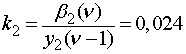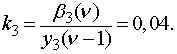(13)

Из формул (13) видно, что коэффициенты и для разных учебных групп подобны друг другу, и их можно усреднить:

Оценка эффективности индивидуального обучения, рассчитанного при решении прямой задачи параметрической оптимизации.

Составление плана индивидуального обучения является завершающей операцией после того, как найдены все параметра критерия, используемого при решении прямой задачи оптимизации для нахождения времени и освоения простого и сложного навыков. Будем исходить из того, что значения и для средней группы, представленные в плане обучения в табл. 1 и 2, уже являются оптимальными.

Таблица 3. Эффективность планирования

Эффективность, %	Сильная группа	слабая группа
сложный навык	9,5	-50,5
простой навык	-1,3	26,2
Суммарная	1,9	11,6
	4,8

Непосредственные расчеты суммарной успеваемости показывают, что в результате оптимизации у сильной группы уровень освоения сложного навыка возрос на 9%, у слабой группы уровень освоения простого навыка возрос на 26,2%.

В целом общая средняя успеваемость может быть повышена за счет индивидуального обучения по максимуму на 10-12%, а это эквивалентно снижению общего времени обучения для достижения заданного уровня обученности и соответственно сокращению стоимости обучения.

Заключение

На основании проведенных исследований можно сделать следующие выводы.

· Предложенные степенные экспоненциальные модели оценки качества обучения позволяют в силу своей обратимости идентифицировать ее параметры по результатам тестирования, т.е. аналитически решить обратную задачу параметрической оптимизации.

· Показана возможность повышения уровня параллельного освоения простых и сложных навыков путем оптимизации планов индивидуального обучения, что приводит к снижению стоимости времени достижения нужного уровня подготовки специалистов.

Литература

1. Глазов Б.И. Параметрический поиск и особенности практического применения шумоподобных сигналов. М.: ВА им. П. Великого, 1974.

2. Горькова В.И. и др. Закономерности роста и старения научно-технической информации и их использование в работе информационных органов. Наука, информация, производство. М.: ВИНИТИ, 1978.

3. Гаас С. Линейное программирование. М.: Физматгиз, 1961.

4. Теория оптимальных систем / Г.Н. Лебедев и др. М.: МАИ, 1999.