BC/NW 2011; №2 (19):10.3

СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ В КОМПЬЮТЕРНЫХ МЕТОДАХ МНОГОМЕРНОЙ КОМБИНАТОРИКИ

Рябов Г.Г.

(Московский государственный университет, Россия)

В предлагаемой работе методы кодирования кубических структур, рассмотренные в [10-12] для n-куба и кубической n-окрестности, развиваются с более общих позиций языкового формализма. Решается вопрос выбора алфавита и его связь с перечислительными задачами на кубических структурах для кубической n-окрестности радиуса r (r-целое) в целях компьютерного конструирования кубических комплексов и многообразий с заданными свойствами. Обсуждается вопрос отображения подмножеств Z на конечные хаусдорфовы метрические пространства, точками которого являются все k-мерные грани n-куба. В заключение обсуждаются вопросы эффективности символьных вычислений при компьютерной реализации. Работа поддержана грантом РФФИ 09-07-12135 офи_м.

Ключевые слова: представления k-граней в n-кубе, метрика Хаусдорфа-Хэмминга, многообразие S³, посимвольные операции.

Введение.

Область задач синтеза геометрико-топологических структур с заданными свойствами постоянно расширяется. Достаточно указать несколько важнейших научно-технических направлений. Триангуляция трехмерного пространства со сложными метрическими и топологическими ограничениями, связанными с условиями задачи и выбранными методами расчета на соответствующих сетках [1], построение многообразия, как общей структуры, в которую отображаются решения частных численных методов. Характерный пример- конформная кубоидная сфера в проекте глобальной циркуляции атмосфера-океан МТИ [2]. Метрико-топологическое размещение электронных элементов и их межсоединений с учетом множества факторов электрического, теплового, конструктивного характера при переходе на трехмерные схемы.

Чем компьютер и его математическое обеспечение может помочь в решении подобных задач? Очевидно, что область структур должна быть хорошо формализована и должен быть создан богатый алгоритмический инструментарий для операций над такими структурами и их составляющими [9].

Последние годы характеризует интерес к так называемой пространственной логике, которая формализует геометрическое взаимное положение объектов в пространстве с помощью языковых конструкций и модальных алгебр. В работе [8] авторы высказывают положение, которое во многом совпадает с целью разработки методов, которым посвящена данная статья: «Надежда состоит в том, что использование языкового формализма, как удобного основания для представления определенного уровня геометрических объектов, позволит устранить трудоемкие машинные действия по их реконструкции в терминах множества точек.»

Основной строительный материал для синтеза – симплициальные и кубические комплексы в течение последних полутора веков прочно рассматривается как самый надежный научный фундамент [3-7]. В дальнейшем изложении основное внимание будет сосредоточено на кубических комплексах, при этом будет рассматриваться решеточное евклидово пространство R_cⁿ, состоящее из стандартных n-кубов с вершинами в целых точках, используя обозначение из [3].

Определения и представления. В пространстве R_cⁿ задан репер 0,е1,е2,…еn. Относительно 0 рассматривается множество всех k-граней, координаты вершин которых удовлетворяют |x_i|<r (в кубической окрестности радиуса r):

F(k,r)={f(k,x): f(k,x)ÎR_cⁿ; |x|£r }.

n

Общее множество всех граней: Ф(n,r)=U F(k,r);

k=0

0-остов R_cⁿ –множество всех целых точек, 1-остов-множество всех единичных ребер с вершинами в целых точках, и т.д. до n-кубов со всеми их гранями.

В [10] показано, что каждая k-грань в n-кубе может быть взаимно однозначно (биективно) представлена в виде n-символьного (разрядного) слова с символами(буквами) из алфавита {0;1;2}. Каждому i-му разряду (а_i) этого слова поставлен в соответствие базисный вектор ei. Cимвол «2» в i-м разряде означает, что единичный интервал I, колинеарный ei, входит как сомножитель в декартово произведение, вместе с еще k-1 единичным интервалом («2» в других k-1 разрядах), образуя грань размерности k. Символы «0» и «1» в остальных разрядах слова отражают сдвиг (трансляцию) вдоль соответствующих базисных векторов. Грубо говоря, такое троичное слово – генетический код создания k-мерной грани и ее места (локальных координат) в n-кубе. Поэтому формально для n-куба:

f(k,x)=ПI(ei) + TS(ej);

i:а_i=2 j:а_j=0;1

|i|=k |j|=n-k.

Отсюда число всех граней в n-кубе равно 3ⁿ, а число k-граней равно С(n,k)2^n-k. Здесь и в дальнейшем C(n,k)-число сочетаний из n по k ( n!/(n-k)!k!)

Троичное слово над этим алфавитом названо кубантом (кубическим квантом).

Эта конструкция в [12] была развита для кубической окрестности радиуса r=1. Для этого был расширен алфавит до пятеричного {-2;-1;0;1;2} и показано, что число всех граней и граней размерности k:

| Ф(n,1)|=5ⁿ; |F(k,1)|=C(n,k)2^k3^n-k.

Пятеричное слово над этим алфавитом названо кросскубантом. На кубантах и кросс-кубантах [10,12] определена бинарная операция посимвольного умножения, которая позволяет вычислить кубант общей грани ( если соответствующие грани имеют непустое пересечение) или длину минимального пути (по ребрам) между гранями, если их пересечение пусто. Для кубантов правила посимвольного умножения (коммутативны):

0Ä0=0;0Ä2=2Ä0=0; 0Ä1=1Ä0=Ø; 1Ä1=1; 1Ä2=2Ä1=1;2Ä2=2, где Ø-пустое множество.

Так, например для 3-куба:

Квадратные грани, кубанты которых (2,2,1) и (2,0,2) в пересечении имеют грань с кубантом (2,0,1), т.е. общее ребро: (2,2,1)Ä(2,0,2)=(2,0,1);

Для квадратной грани (2,2,1) и ребра (2,1,0): (2,2,1)Ä(2,1,0)=(2,1,Ø)-пересечение пусто и длина минимального пути между этими гранями равна 1.

На гранях n-куба определена хаусдорфова метрика, которая является обобщением хэмминговой метрики для двоичных кодов (rНН) и приведен алгоритм ее вычисления, используя посимвольные операции над кубантами (сложность О(n)). [10,11] Аналогичным образом можно рассматривать грани из Ф(n,1) как точки конечного метрического НН-пространства.

Таким образом, ответ на вопрос о связности граней и расстоянии между ними заключается в вычислениях над соответствующими кубантами (как генетическими кодами этих граней). Рассмотрены и другие операции, сводящиеся к вычислениям на кубантах, так что можно условно говорить об алгебре кубантов.

Дальнейшим развитием подхода является формализация представления граней в множестве Ф(n,r) при r>1.

На вещественной прямой R рассматривается два множества : множество целых точек

{-r;-r+1;…-1;0;1;…r} и множество единичных интервалов между ними

{[-r;-r+1],[-r+1;-r+2],…[-1;0],[0;1],…[r-1;r]}.

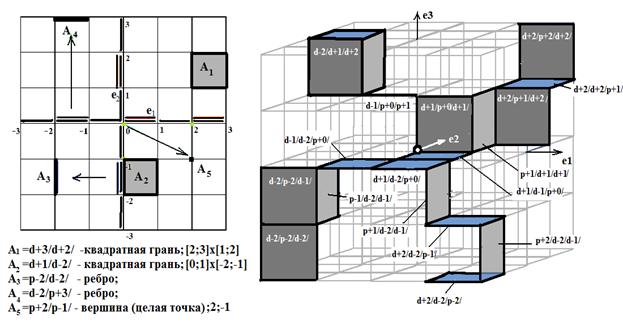
Рис.1. Кубическая 2-окрестность радиуса 3 и примеры представления граней (а); 3-комплекс в 3-окрестности радиуса 2 и представления его граней (б).

Будем считать, что каждой точке соответствует некоторая 2r+1 буква из алфавита, а каждому интервалу 2r других букв, так что общий алфавит содержит 4r+1 букв. Для прозрачности излагаемых построений будем оперировать с условными буквами, состоящими из нескольких символов, которые однозначно соответствуют точкам и единичным отрезкам, считая их за буквы для слов фиксированной длины n. В таких словах номер буквы в слове, считая слева направо и начиная с 1, будем иногда называть номером разряда n-разрядного (4r+1)-ичного слова.

Примем для наглядности следующую, наиболее прозрачную форму нотации. Каждая такая буква имеет следующий однородный вид- признак, целое число, разделитель; здесь признаком р обозначается целая точка, d-единичный отрезок и m-длина пути (в единичных отрезках) между парой точек, точкой и отрезком, двумя отрезками. Целое число, следующее за признаком р равно координате точки на прямой, при признаке d максимальной по модулю координате интервала и числу единичных интервалов при признаке m (рис.1). Таким образом, буквы могут иметь вид:

р-3 ; d+2 ; d-1 ; m5 ; что соответствует точке -3; интервалам[1;2] и [0;-1]; длине минимального пути, равного 5 (например, между р-3 и р+2). Между буквами в слове применяется разделитель /.

Все n-разрядные слова с буквами из 4r+1-ичного алфавита биективны всем граням размерностей от 0 (целые точки) до n (n-мерный единичный куб)

n

в области: П 2rI(ei), где П-декартово произведение, 2rI(ei) –интервал

i=1

[-r;r] вдоль ei .

Отсюда непосредственно следует, что общее число граней для кубической n-окрестности радиуса r равно |Ф(n,r)|=(4r+1)ⁿ, а число граней размерности k равно |F(n,r,k)|= C(n,k) (2r)^k (2r+1)^n-k .

Поскольку в данном случае рассматривается обобщение, то целесообразно в дальнейшем ограничиться для рассматриваемого множества слов общим названием кубанты. Кубант для Rcn это слово из n букв из конечного алфавита (при рассмотрении компьютерных реализаций можно говорить не о «букве», а о «разряде», разумеется не двоичном, код которого представляет букву). Поскольку излагаемые вопросы находятся на стыке формальных языков, кодирования и компьютерных реализаций оправдано некоторое терминологическое смешение. Так буква алфавита и символ, номер буквы в слове и номер разряда в слове.

По аналогии с [10,12] вводится операция умножения. Ниже приведена таблица (в связи с коммутативностью умножения показана ее половина) поразрядного(посимвольного) умножения (Ä) для кубической окрестности радиуса 3, которая по сути представляет фрагмент интервальной арифметики.

р-3

d-3

p-2

d-2

p-1

d-1

p0

d+1

p+1

d+2

p+2

d+3

p+3

р-3

р-3

р-3

m1

m1

m2

m2

m3

m3

m4

m4

m5

m5

m6

d-3

d-3

p-2

p-2

m1

m1

m2

m2

m3

m3

m4

m4

m5

p-2

p-2

p-2

m1

m1

m2

m2

m3

m3

m4

m4

m5

d-2

d-2

p-1

p-1

m1

m1

m2

m2

m3

m3

m4

p-1

p-1

p-1

m1

m1

m2

m2

m3

m3

m4

d-1

d-1

p0

p0

m1

m1

m2

m2

m3

p0

p0

p0

m1

m1

m2

m2

m3

d+1

сим

мет

рия

d+1

p+1

p+1

m1

m1

m2

p+1

p+1

p+1

m1

m1

m2

d+2

d+2

p+2

p+2

m1

p+2

p+2

p+2

m1

d+3

d+3

d+3

p+3

p+3

Основные свойства произведения двух кубантов А и В:

1. Если грани, соответствующие А и В имеют общую грань, то АÄВ равно кубанту С и соответствует общей грани.

2. Если нет общей грани, то С содержит буквы с признаком m. Сумма чисел в буквах с признаком m равна длине минимального пути (по ребрам) Lmin(A;B) между гранями, соответствующим кубантам А и В.

В дальнейшем комплекс из кубантов в n-окрестности радиуса r будем обозначать Q(n,r). Размерность комплекса будем считать равной максимальной размерности грани (кубанта), включенного в комплекс. Так комплекс Q(3;2)={A₁,A₂,…A₁₇} есть 3-комплекс в 3-окрестности радиуса 2. (рис.1, б). Для этого комплекса:

А₁= d+2/p+2/d+2/; А₂=d+2/d+2/p+1/; … А₁₇=d-2/p-2/d-2/;

А₁ÄА₂= d+2/p+2/p+1/; (общая грань-ребро);

А₁ÄА₁₇= m2/m4/m2/; à Lmin(A₁;A₁₇)=8.

Вычисление хаусдорфовой-хэмминговой (НН) метрики. Обобщая алгоритмы вычисления r_НН, изложенные в [11], рассмотрим произведение двух произвольных кубантов А и В и поразрядные действия для вычисления р_НН. Итак рассматриваются AÄВ* и A*ÄВ, где * означает, что в разрядах помеченного кубанта перед самим действием умножения могут происходить изменения в зависимости от значений соответствующих разрядов другого кубанта. Пусть х,у- положительные целые и х£r;y£r; тогда эти изменения в разрядах (для АÄB*) проводятся по следующим правилам:

1. a_i=p+x; b_i=d+y; x³y;àa_i*=p+(y-1);

x<y;à a_i*=p+y;

2. a_i=d+x; b_i=d+y; x>y; à a_i*=p+(y-1);

x<y;à a_i*=p+y;

3. a_i=p+x; bi=d-y;àa_i*=p-y;

4. a_i=p-x; b_i=d-y; x>y;àa_i*=p-(y-1);

x<y;àa_i*=p-y;

5. a_i=p-x; b_i=d+y;àa_i*=p+y;

6. a_i=d-x; b_i=d-y; x>y;àa_i*=p-(y-1);

x<y;àa_i*=p-y.

В остальных случаях изменений не происходит.

Затем следует операция АхВ* и вычисляется Lmin(AxB*). Аналогично вычисляется Lmin(A*xB) и окончательно: r_HH(A,B)=max{Lmin(AxB*),Lmin(A*xB)}.

Cледуя этим правилам для кубантов из вышеприведенного примера, получим:

r_НН(А₁,А₂)=1; r_HH(A₁,A₁₇)=10; r_HH(A₂,A₁₇)=9.

Отметим, что комплексу Q cоответствует частично упорядоченное множество r_НН для всех пар A_i,A_jÎ Q, которое инвариантно относительно движений, сохраняющих структуру Q в R_cn.

Вычисление r_НН(Q₁,Q₂) между комплексами реализуется через вычисления всех r_НН(A_1i,A_2j); A_1iÎQ₁,A_2jÎQ₂; и последующими действиями в соответствии с определением хаусдорфовой метрики:

r_HH(Q₁,Q₂)=max{max {Lmin (A_1i*,A_2j)},max{L min (A_1i,A_2j*)}}.

Q₂ Q₁

О направлениях развития вычислений на кубантах.

Одним из направлений развития в предлагаемой тематике является общий конструктивный подход к генерации многообразий на основе кубических структур, который можно представить в последовательности следующих этапов.

1. Выбор размерности и радиуса кубической окрестности для конструирования исходного кубического комплекса, в котором атлас карт строящегося многообразия будет соответствовать исходным требованиям. Отсюда однозначно следует размер алфавита и кодирование граней.

2. Формальное (языковое) описание кубического комплекса (как множества кубантов) на k-мерных гранях с использованием метрико-топологических зависимостей НН-метрики).

3. Применение к комплексу оператора границы и получение кубического многообразия (кубильяжа) с атласом карт заданного типа.

4. Проецирование кубического многообразия на гладкие тела, заданные аналитическими выражениями или кусочно-гладкими представлениями (составляющими). Представление псевдокубических граней многообразия.

5. Проведение дополнительной дискретизации составляющих многообразие.

Такой подход изложен в [12] на примере построения многообразия трехмерной сферы S³ единичного радиуса. Приведем сравнительную «анатомию» кубической 4-окрестности при r=1 и созданной на ее основе такой сферы.

Вершины Ребра 2-грани 3-грани 4-грани

Кубическая 4-окрестность 81 216 216 96 16

3-мерная сфера 80 208 192 64 0

Другим направлением развития может стать отображение целых чисел на кубические n-окрестности радиуса r. Для пояснения рассмотрим 3-окрестность радиуса r=1. Все грани такой окрестности однозначно кодируются 3-разрядными пятеричными числами. В предложенной нотации алфавит выглядит как {p-1,d-1,p0,d+1,p+1}. Поставим этому алфавиту в однозначное соответствие следующий алфавит {0;1;2;3;4}, т.е. значения разрядов в обычной пятеричной системе представления чисел. Тогда каждому кубанту (грани) будет однозначно соответствовать целое число из интервала [ 0; 5³-1], т.е. числа от 0 до 124. Значительная часть такого отображения показана на рис. 3, а). Поскольку на гранях определена НН-метрика, то ее можно отнести к соответствующим этим граням целым числам. И вообще рассматривать эти целые числа как номера граней. Так на рис. 2 показан лист мебиуса на квадратных гранях, для которого этот комплекс закодирован как множество чисел в десятичной записи {44;38;32;56;80;90;116;118;94}.

При десятичной записи обратный перевод осуществим через запись числа в пятеричном виде. Разумеется, что такое отображение возможно для произвольных n,r .

Несколько элементарных свойств таких отображений при любых n и r:

1. Четные числа соответствуют граням четной размерности (включая 0), нечетные числа-граням нечетной размерности.

2. Число, соответствующее k-грани, равно полусумме чисел параллельных любых двух

k-1-граней на границе этой грани. Отсюда сумма чисел всех граней границы, деленная на число граней в границе, также равна числу этой k-грани.

3. При заданном r обозначим множества чисел, относящихся к интервалам [0;(4r+1)ⁿ-1]при n=1,2…N и однозначно отображаемых в n-окрестности через Z_n(r). Тогда Z₁(r)ÌZ₂(r)Ì…

Z_n-1(r)ÌZ_n(r)Ì… , т.е. НН-метрика на отображенных числах инвариантна относительно размерности n. Или грубо говоря, увеличивая диапазон чисел и переходя к отображению в следующую размерность отображение в предшествующую размерность сохраняется.

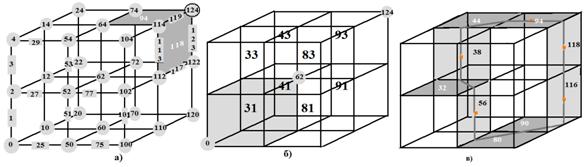
Рис. 2. Отображение множества натуральных чисел [0;124] на k-грани 3-окрестности радиуса r=1 (а, б); лист Мебиуса на квадратных гранях с отображенными числами (в)

О компьютерной реализации. Вычисления на кубантах можно отнести к разряду символьных, которые обладают следующими свойствами:

1. При увеличении размерности пространства кубических структур алфавит остается без изменений.

2. Увеличение объема алфавита связано только с увеличением радиуса кубической n-окрестности.

3. Введение составных букв (признак + целое число) позволяет не ограничивать объем алфавита и иметь точные числа при перечислении граней любой размерности при произвольном r для кубической n-окрестности (4r+1-ичное кодирование).

4. Основная операция умножения является посимвольной и поэтому имеет сложность О(n), где n-число символов (букв) в кубанте.

5. Алгоритм вычисления НН-метрики для кубантов (граней) в основе своей также имеет посимвольные операции и поэтому имеет сложность О(n).

6. Для машинного представления букв кубантов может быть выбран вариант чисел, отображенных на грани n-окрестности радиуса r в 4r+1-ичном виде.

Следует подчеркнуть, что посимвольный характер операций дает возможность использовать групповые операции над множеством символов одновременно при хранении кубантов в памяти в виде байтовых стрингов. При этом каждый такой стринг может иметь кольцевой сдвиговый (на целое число байтов) механизм, который позволит производить вычисление произведений всех пар кубантов, принадлежащих двум разным комплексам следующим образом.

Пусть Q₁={ A₁,A₂,…A_s}; Q₂={B₁,B₂,…B_s}; и необходимо вычислить матрицу:

| A₁ÄB₁ A₂ÄB₂ … A_s-1ÄB_s-1 A_sÄB_s |

| A₁ÄB₂ A₂ÄB₃ … A_s-1ÄB_s A_sÄB₁ |

Q₁ÄQ₂ = | … |

| A₁ÄB_s A₂ÄB₁ … A_s-1ÄB_s-2 A_sÄB_s-1 |

Каждая строка матрицы вычисляется как одна посимвольная операция умножения двух стрингов. Затем сдвиг на число байтов, соответствующих одному кубанту и новое умножение. Таким образом матрица вычисляется за 2s операций. Число кубантов в матрице (без букв, соответствующих m из табл. 1)  ‑ это множество общих граней у комплексов Q₁ и Q₂. В случае если это множество пусто, то минимальное число положительное число (не может быть 0, т.к. тогда пересечение не пусто) есть Lmin(Q₁,Q₂)

Для определения р_НН(Q1,Q2) вычисляются аналогичным образом две матрицы Q₁*ÄQ₂ c элементами A_i*ÄB_j и Q₁ÄQ₂* с элементами A_iÄB_j*. В этом случае каждая строка вычисляется за 3 операции и вся матрица за 3s операций. Из каждой матрицы выбирается наибольший элемент из s2 элементов и затем наибольший из этих двух. Если иметь операцию определения максимального элемента в строке, то общее число операций составит 2(3s +s)=8s.

Эти оценки позволяют сделать вывод об эффективности вычислений, в которых алгебраическое представление и посимвольная обработка практически реализует параллельные вычисления над множествами кубических структур, не разлагая их до множеств точек. Так с ростом размерности пространства сложность операций растет линейно, в то время как число элементов в рассматриваемых структурах растет экспоненциально. Это открывает путь к решению прикладных комбинаторных задач большой размерности. Применяя такие методы посимвольной обработки на суперкомпьютере МГУ «Чебышев» рассчитаны матрицы всех парных НН-расстояний для граней кубических окрестностей для размерностей n =2-10 [11].

Более детальная информация и графическая интерпретация рассматриваемых методов приведена на сайте http://www.vizcom.srcc.msu.ru

Литература

1. Четверушкин Б.Н., Шильников Е.В. Вычислительный и программный инструментарий для моделирования трехмерных течений вязкого газа на многопроцессорных системах // Ж. вычисл. матем. и матем. физики.48:2(2008), 309-320.

2. Marshall J., Adcroft A., Campin J-M., Hill C. Atmosphere-Ocean modeling exploiting fluid isomorphisms // Boston.MIT.2002.

3. Долбилин Н.П., Штанько М.А., Штрогин М.И. Кубические многообразия в решетках // Изв. РАН. Сер. матем. 1994. 58. Вып. 2. С. 93-107.

4. Деза М.А., Штрогин М.И. Вложение графов в гиперкубы и кубические решетки // Успехи матем.наук.1997. 52. №6.155-156.

5. Бухштабер В.М., Панов Т.Е. Торические действия в топологии и комбинаторике. МЦНМО. 2008.

6. Gaifullin A.A. Construction of combinatorial manifolds with the prescribed sets of links of vertices // arXiv:0801.4741v1 [math.GT] 30 Jan 2008.

7. Stanley R. Combinatoric and Commutative Algebra.//Birkhauser.1996.

8. Kontchakov R., Pratt-Hartmann J., Wolter F., Zakharyaschev M. Spatial Logics and Connectedness Predicates // Log. Methods in Comp.Science. Vol.6(3:5)2010.1-43.

9. Manin Yu.I. Classical computing, quantum computing and Shor’s factoring algorithm.// arXiv: quant-ph/99 05008v1/2 March 1999.

10. Рябов Г.Г. О четверичном кодировании кубических структур // Вычислительные методы и программирование. 2009. Т.10.
340-347.

11. Рябов Г.Г. Хаусдорфова метрика на гранях n-мерного куба // Фундаментальная и прикладная математика.16:1(2010), 151-155.

12. Рябов Г.Г., Серов В.А. О метрико-топологических вычислениях в конструктивном мире кубических структур // Вычислительные методы и программирование. 2010. Т.11. 326-335.