BC/NW 2011; №2 (19):4.1

АЛГОРИТМЫ ПЛАНИРОВАНИЯ ВЫПОЛНЕНИЯ ПАКЕТА ЗАДАНИЙ В РАСПРЕДЕЛЕННЫХ ВЫЧИСЛИТЕЛЬНЫХ СРЕДАХ

Топорков В.В., Бобченков А.В., Емельянов Д.М.

(Национальный исследовательский университет «МЭИ», Россия)

Введение

Экономические модели выделения ресурсов и планирования являются весьма эффективными в распределенных вычислениях с неотчуждаемыми ресурсами, включая грид, мультиагентные системы и облачные вычисления [1; 2].

В [4] рассматриваются эвристические алгоритмы поиска наборов слотов на основе задаваемых пользователем функций полезности.

Среди различных подходов к организации вычислений в распределенных системах и средах можно выявить две устойчивые тенденции.

Одна из них основывается на использовании брокеров ресурсов [3; 4], которые, как правило, позволяют оптимизировать выполнение конкретного приложения [5].

Другая тенденция связана с образованием виртуальных организаций и ориентирована прежде всего на грид-системы. При образовании виртуальных организаций [6] осуществляется оптимизация планирования на уровне потоков заданий. В рамках предложенной модели планирования потоков заданий [7], важным этапом является предварительный поиск альтернативных вариантов назначения выполнения каждого из заданий.

Новизна подхода состоит в применении экономических механизмов как на этапе отбора альтернативных наборов слотов, так и на этапе планирования выполнения пакета заданий.

Схема планирования

В рамках рассматриваемой модели, в основу которой заложена иерархическая схема управления потоками заданий [5; 6], фигурируют пользователи, запускающие задания, и собственники вычислительных ресурсов. Планирование выполнения совокупности (пакета) независимых заданий осуществляется циклично, на основе динамично обновляемых расписаний выполнения заданий в локальных процессорных узлах (рис. 1).

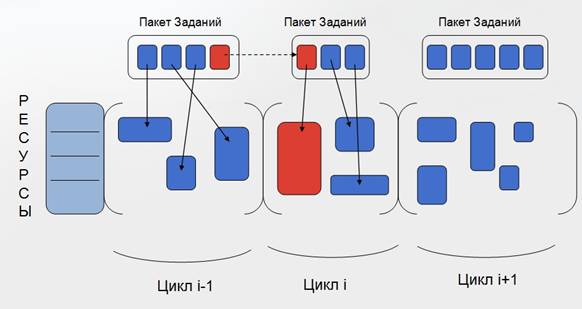
Рис. 1. Планирования потока заданий на основе циклов

В каждом цикле планирования запуска пакета заданий требуется решение двух задач. Во-первых, отбор подходящих (по ресурсу, времени, цене) слотов для каждого задания пакета [4] (в общем случае у каждого задания может оказаться несколько альтернативных наборов слотов для выполнения - альтернатив). Во-вторых, необходим выбор комбинации альтернатив, являющейся эффективной или оптимальной с точки зрения прохождения всего пакета заданий в текущем цикле планирования.

В данной работе мы рассматриваем два типа критериев и две задачи однокритериальной оптимизации выполнения пакета заданий. Это минимизация стоимости выполнения пакета заданий при ограничении на суммарное время занятия слотов, либо минимизация времени прохождения пакета заданий при фиксированном бюджете виртуальной организации.

Алгоритмы отбора слотов

В начале каждого цикла динамично обновляются наборы доступных слотов на основе информации, поступающей от локальных менеджеров ресурсов. Каждый из слотов соответствует временному отрезку, который может быть использован для выполнения задачи, входящей в состав многопроцессорного задания, на том или ином типе ресурса. Требования задания к ресурсам оформляются в виде ресурсного запроса, содержащего тип, количество и характеристики узлов (тактовую частоту процессора, емкость оперативной памяти, дисковое пространство, операционную систему и т.д.), а также оценку времени их использования. Кроме того, пользователь указывает максимальную удельную стоимость за использование отдельного узла, которую он готов заплатить. В рассматриваемой нами модели пользователь также указывает минимальную допустимую производительность P узлов, подходящих для выполнения его задания. Для запуска многопроцессорного задания необходимо согласованное выделение требуемого для его выполнения слотов. В случае однородных узлов совокупность слотов для выполнения задания представляет собой прямоугольное «окно» размером , а для процессоров с разной производительностью это – «окно» с неровным правым краем, где – время выполнения составной части задания на наименее производительном процессоре (рис. 2).

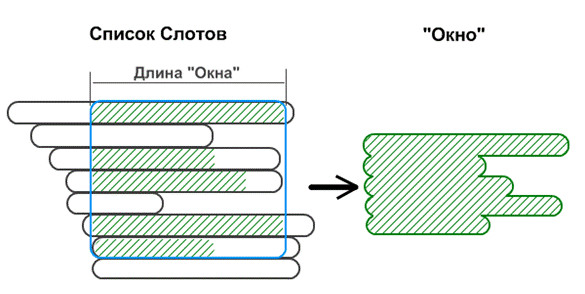
Рис. 2. Формирование окна с неровным правым краем

Нами рассматриваются два алгоритма поиска альтернативных наборов слотов.

Первый из них ALP, производит поиск окна на упорядоченном по неубыванию времени старта списке слотов системы. Его особенность состоит в том, что он учитывает ограничение на максимальную удельную стоимость каждого отдельного слота. Приведем описание алгоритма ALP:

1°. Доступные слоты системы упорядочиваются по неубыванию времени старта.

2°. Из полученного списка выбирается следующий подходящий слот . Слот считается подходящим, если удовлетворяет следующим требованиям:

a) производительность узла, на котором выделен слот ;

b) длины слота достаточно, чтобы выполнить часть многопроцессорного задания (с учетом актуальной производительности узла) ;

c) удельная стоимость использования слота не выше ограничения .

Если условия a), b) и c) выполняются, то слот добавляется в список слотов окна.

3°. Время старта всего окна полагается равным времени старта последнего добавленного слота. Далее происходит проверка всех текущих слотов списка окна. Если с учетом нового общего времени старта длины слота уже не хвататет, чтобы выполнить часть задания (пункт 2°b), этот слот удаляется из списка слотов окна и в дальнейшем не рассматривается.

4°. Если число оставшихся слотов в списке окна меньше , то переход на шаг 2°.

5°. Конец алгоритма.

В случае, если до конца списка слотов системы мы не смогли найтиподходящих слотов, то считается, что окно найти не удалось и задание переносится в следующий цикл планирования.

Стоит отметить, что данный подход с ограничением на удельную стоимость отдельных слотов сужает область поиска и не позволяет использовать для составления окна более дорогие слоты. Отличие следующего алгоритма AMP состоит в том, что он оперирует с ограничением на максимальный бюджет выполнения задания. Максимальный бюджет формируется как , где - необходимое время резервирования; - запрашиваемое количество слотов, а - указанное в ресурсном запросе ограничение на удельную стоимость отдельного слота. Таким образом, алгоритм AMP производит поиск окна, суммарная стоимость слотов которого не превышает максимальный бюджет.

При описании алгоритма AMP мы воспользуемся дополнительными обозначениями: – текущее количество слотов в списке окна; – суммарная стоимость первых слотов окна.

Рассмотрим алгоритм AMP для поиска отдельного окна:

1°. Находится самое ранне окно из слотов, используя алгоритм ALP без учета условия 2°c.

2°. Слоты внути списка окна упорядочиваются по возрастанию их стоимости.

Далее вычисляется суммарная стоимость первых слотов окна. Если , то к шагу 4°, в этом случае результирующее окно формируетсся из первых слотов, а остальные возвращаются в список слотов системы. Иначе к шагу 3°.

3°. Добавляется следующий подходящий слот из списка с учетом ограничений 2°a и 2°b алгоритма ALP. Время старта формируемого окна полагается равным времени старта этого слота. Далее проверяется, все ли слоты успевают выполнить задание с учетом нового времени старта, а те, которые не успевают, удаляются (шаг 3° алгоритма ALP).

Если , то повтор шага 3°. Если , то к шагу 2°.

Если список слотов системы закончен и, то найти окно не удалось.

4°. Конец алгоритма.

Следует отметить следующие три особенности предлагаемых алгоритмов. Во-первых, оба алгоритма учитывают производительность и разнородность вычислительных узлов. Это позволяет формировать окна с неровным правым краем. Во-вторых, оба алгоритма учитывают экономические ограничения пользователя: ограничение на максимальную допустимую удельную стоимость использования ресурсов. В-третьих, оба алгоритма обладают линейной сложностьюотносительно общего количества слотов системы , алгоритмы двигаются по списку слотов в направлении неубывания времени старта, без возвращения назад и пересмотра предыдущих шагов.

Результаты моделирования

Эксперимент состоит в сравнении результатов планирования пакета заданий на одинаковом наборе ресурсов, но с использованием различных алгоритмов поиска альтернативных наборов слотов ALP и AMP. На каждом цикле планирования происходит генерация исходных данных: списка доступных слотов системы и пакета пользовательских заданий. Рассмотрим задачу поиска альтернативынх наборов слотов при минимизации суммарного времени выполнения пакета заданий с ограничением на общий бюджет .

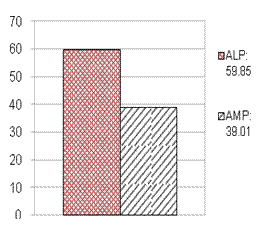
(а) (б)

Рис. 3. Минимизация времени выполнения пакета заданий: среднее время выполнения задания (a); средняя стоимость выполнения задания (б)

В общей сложности было промоделировано 25000 циклов планирования. Для подсчета результатов использовались только те из них, в которых все задачи пакета имели хотя бы одну альтернативу выполнения. По результатам моделирования алгоритм AMP превзошел ALP по целевому критерию минимизации суммарного времени выполнения пакета заданий на 35%. Среднее время выполнения одного задания при использовании ALP составиоло 59.85, а при использовании AMP - 39.01 (рис. 3, a).

При этом средняя стоимость выполнения задания с использованием ALP составила 313.56, а для AMP на 15% больше - 369.69 (рис. 3, б).

При решении минимизации суммарной стоимости выполнения пакета заданий: с ограничением на суммарное время выполнения _, были собраны результаты 8571 отдельных циклов планирования, в каждом из которых все задания имели хотя бы по одной альтернативе выполнения.

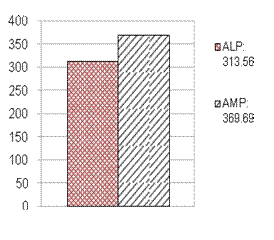
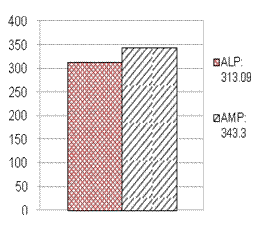
Средняя стоимость выполнения задания в схеме с использованием алгоритма ALP составила 313.09, а при использовании AMP - 343.3, что демонстрирует преимущество алгоритма ALP в 9% (рис. 4, a). Более высокая стоимость объясняется тем, что алгоритм AMP стремится использовать весь доступный бюджет задания и в среднем находит более дорогие по сравнению с алгоритмом ALP альтернативы.

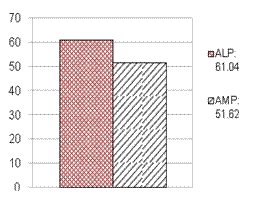
Среднее же время выполнния задания для ALP составило 61.04, а с использованием AMP - 51.62, что на 15% меньше (рис. 4, б).

(а) (б)

Рис. 4. Минимизация стоимости выполнения пакета заадний: средняя стоимость выполнения задания (a); среднее время выполнения задания (б)

При этом среднее количество слотов в отдельном эксперименте составило 135.2. Это число совпадает со средним количеством слотов по всем 25000 экспериментам, что говорит об отсутствии решающего влияния общего количества слотов на результаты поиска альтернатив. Общее количество найденных альтернатив алгоритмом ALP равно 253855 или в среднем 7.28 на задание. Алгоритм AMP при этом нашел 1154116 альтернативы или 34.23 на задание.

Стоит отдельно отметить, что в ходе проведения эксперимента, алгоритм AMP позволял находить в среднем в 4-5 раз больше альтернатив выполнения для каждого задания, чем ALP, на одном и том же наборе ресурсов. Отчасти этим и объясняется его преимущество: на этапе планирования большее количество альтернатив позволяет выбрать более эффективную их комбинацию.

Заключение

Предложены и рассмотрены алгоритмы поиска альтернативных наборов слотов в контексте модели управления потоками заданий на основе иерархической структуры виртуальной организации распределенной вычислительной среды. Алгоритмы учитывают разнородность среды и действующие экономические механизмы. С помощью проведенного моделирования, были рассмотрены преимущества и недостатки использования этих алгоритмов на этапе поиска подходящих наборов слотов.

Литература

1. Garg S.K., Buyya R., Siegel H.J. Scheduling parallel applications on utility Grids: time and cost trade-off management, Proceedings of the 32nd Australasian computer science conference (ACSC 2009), Wellington, New Zealand.

2. Bredin J., Kotz D., Rus D. Economic markets as a means of open mobile-agent systems, Proceedings of the workshop “Mobile agents in the context of competition and cooperation (mac3)”, 1999.

3. Buyya R., Abramson D., Giddy J. Economic models for resource management and scheduling in grid computing // J. of concurrency and computation: practice and experience. Vol. 14, no. 5, 2002.

4. Ernemann C., Hamscher V., Yahyapour R. Economic scheduling in grid computing. In: Proceedings of the 8th job scheduling strategies for parallel processing, D.G. Feitelson, L. Rudolph, U. Schwiegelshohn (eds.), Springer, Heidelberg, LNCS. Vol. 2537, 2002.

5. Toporkov V. Application-level and job-flow scheduling: an approach for achieving quality of service in distributed computing, Proceedings of the 10th international conference on parallel computing technologies, Springer, Heidelberg, LNCS. Vol. 5698. 2009.

6. Kurowski K., Nabrzyski J., Oleksiak A. et al. Multicriteria Aspects of Grid Resource Management // In: J. Nabrzyski, J.M. Schopf, and J. Weglarz (eds.), Grid resource management. State of the art and future trends. - Boston: Kluwer Academic Publishers, 2003.

7. Топорков В.В, Топоркова А.С., Целищев А.С., Бобченков А.В., Емельянов Д.М. Масштабируемые модели планирования и управления потоками заданий в распределенных вычислениях // Научный сервис в сети Интернет: масштабируемость, параллельность, эффективность: Труды Всероссийской суперкомпьютерной конференции. - М.: Изд-во МГУ, 2009.