BC/NW 2011; №2 (19):5.2

ОПРЕДЕЛЕНИЕ КОНФИГУРАЦИИ ВЫЧИСЛИТЕЛЬНЫХ КОМПЛЕКСОВ ВЫСОКОПРОИЗВОДИТЕЛЬНОЙ ОБРАБОТКИ БОЛЬШИХ ОБЪЕМОВ ДАННЫХ

Ю.Н. Домаров, В.О. Рыбинцев

(НИУ «Московский энергетический институт»)

Высокопроизводительные вычислительные комплексы активно проникают сегодня во все сферы человеческой деятельности, позволяя успешно решать все более трудные научные и производственные задачи, сопряженные со сложнейшими вычислениями. Такие задачи относят к классу высокопроизводительных вычислений (high-performance computing, HPC), а для их решения используются специализированные суперкомпьютерные системы [1, 2], построенные на базе сотен процессоров. Из всего множества задач HPC особо выделяются такие, решение которых помимо выполнения трудоемких вычислений связано с переработкой огромных объемов данных, исчисляемых терабайтами. Типичными примерами таких задач являются задачи геофизики (обработка данных сейсморазведки, моделирование климатических процессов). Специфика данного класса задач заключается в том, что для их решения необходим не только высокопроизводительный вычислительный кластер (ВК), но и высокоскоростная система хранения данных (СХД). При выборе конфигурации вычислительной системы, состоящей из ВК и СХД, возникает задача комплексной оценки ее производительности для определения согласованных между собой технических характеристик кластера и системы хранения. Причем практическое применение таких систем показало, что увеличение вычислительной мощности кластера часто не только не приводит к росту общей производительности, но и дает обратный эффект [3, 4].

В данной статье приводится математическая модель вычислительного комплекса (как сети массового обслуживания), а также описывается метод определения оптимальной (по критерию производительности) конфигурации комплекса на основе результатов стандартных промышленных тестов производительности ВК и СХД.

Комплекс для решения задач высокопроизводительной обработки больших объемов данных включает в себя вычислительный кластер и систему хранения данных, подключаемую посредством высокоскоростной коммутационной среды (FibreChannel или InfiniBand). Кластер представляет собой набор стандартных многопроцессорных (многоядерных) параллельных вычислительных узлов, объединенных высокоскоростной коммуникационной сетью. Система хранения – RAID массив дисковых устройств, разбитый на определенное число виртуальных томов. Предполагается, что узлы ВК и тома СХД в процессе работы загружаются равномерно.

Отметим также важные особенности рассматриваемого класса задач. Во-первых, объем обрабатываемых данных существенно превышает объем памяти вычислительных узлов, поэтому все данные разбиваются на равные блоки фиксированного размера, распределяемые по томам СХД, а процесс решения задачи разделяется на циклы таким образом, что один узел ВК обрабатывает один блок данных за один цикл. Количество циклов при этом много больше, чем число узлов кластера. В каждом цикле информация проходит в системе по замкнутому контуру: сначала исходные данные считываются с дисков системы хранения и загружаются в узлы кластера, затем они обрабатываются вычислительным узлом, после чего результаты записываются на диск. Процесс решения задачи показан на временной диаграмме (рис. 1). Во-вторых, все блоки данных идентичны (любой узел ВК может обрабатывать любой блок данных) и независимы, что исключает необходимость обмена информацией между вычислительными узлами. В-третьих, время инициализации задачи (распределения заданий по узлам ВК и блоков данных по томам СХД) пренебрежимо мало по сравнению с общим временем решения задачи. Задержками, связанными с образованием очередей в коммутаторе также можно пренебречь, так как в качестве коммутационной среды используются высокоскоростные интерфейсы, пропускная способность которых на порядок больше чем пропускная способность узлов ВК и контроллера СХД.

Рис. 1. Временная диаграмма решения задачи

RD –время чтения одного блока данных;

WR –время записи одного блока данных;

CALC – время счета одного блока данных.

Предлагаемая математическая модель комплекса представлена на рис. 2.

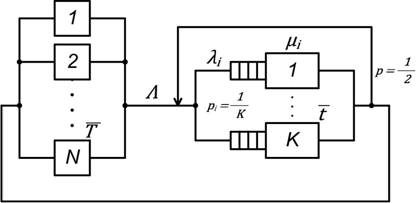
Рис. 2. Математическая модель вычислительного комплекса

Математическая модель представляет собой замкнутую стохастическую сеть массового обслуживания (СеМО). Источником заявок в сети являются N узлов (ядер) ВК. Все заявки поступают в СХД, представленную как K независимых томов, причем каждая заявка проходит ее дважды (что моделируется петлей обратной связи с вероятностью 0.5).

Важно отметить, что распределение времени обслуживания заявок в системе хранения является существенно не экспоненциальным. Поток заявок на входе и соответственно распределение интервалов времени поступления заявок в систему хранения также не является экспоненциальным. Система хранения представляется набором независимых томов, каждый из которых имеет собственную неограниченную очередь. Исходя из всех перечисленных особенностей рассматриваемой системы, для расчета математической модели необходимо использовать формулы для системы массового обслуживания общего вида GI/G/1. Однако точных соотношений, описывающих параметры систем такого рода нет, поэтому при аналитических расчетах обычно используются приближенные соотношения, предложенные в [5].

Используя метод контуров [6, 7] можно составить нелинейное уравнение баланса заявок в сети. Рассматриваемый в модели контур замкнутый, а источниками заявок являются только вычислительные узлы (причем новая заявка от каждого узла генерируется только после обработки предыдущей заявки того же узла). Уравнение баланса:

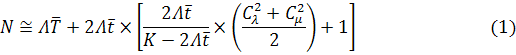
Решение уравнения (1) относительно Λ позволит определить значения Λ и другие средние характеристики функционирования СеМО.

Для нахождения оптимальной конфигурации комплекса (числа ядер ВК и томов СХД), при котором время решения задачи будет минимально, нужно сформировать целевую функцию и решить задачу оптимизации. Целевой функцией будет являться зависимость общего времени решения задачи от параметров СеМО.

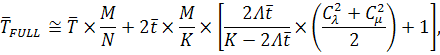
где M – количество циклов.

В данном случае минимизация времени решения всей задачи равносильна минимизации среднего времени одного цикла, а целевая функция принимает вид:

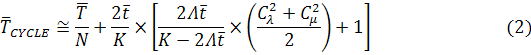
Для нахождения экстремума целевой функции необходимо найти первую производную по переменной N, а затем приравнять выражение для производной к нулю и найти решение полученного уравнения. Для вычисления дифференциала целевой функции по N нужно подставить в нее выражение Λ(N), которое определяется из нелинейного уравнения баланса заявок в системе (1). Подстановка этого выражения в функцию (2) с последующим дифференцированием приводит к алгебраическому уравнению высшей степени относительно N, которое не имеет аналитического решения, а потому прямое решение оптимизационной задачи невозможно. Однако целевую функцию можно существенно упростить, с учетом особенностей рассматриваемого класса задач.

Сначала рассмотрим зависимость Λ(N). Как видно из уравнения (1) Λ зависит от N, а также от T,t и К. Построим качественно график функции f=Λ(N). Он представлен на рис. 3.

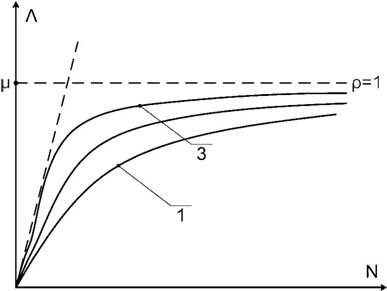
Рис. 3. График функции f=Λ(N)

Для графика 1 соотношение меньше чем для графика 3.

Вид графика зависит от соотношения величин T и t. Чем больше отношение времен T/t, тем более крутой график, и что самое главное тем ближе график приближается к своим асимптотам, одной из которых является прямая ρ=1 соответствующая максимальной загрузке СМО. Второй асимптотой является прямая: . Поскольку при решении задач HPC время расчета существенно превосходит время ввода-вывода, то загрузка СХД далека от единицы, а для приближенных вычислений можно использовать асимптотическое значение:

Кроме того, в выражении (2) можно упростить слагаемое, содержащее коэффициенты вариации. Во-первых, как показано в работе [8] коэффициент вариации для дискового массива (RAID-5 с включенной балансировкой нагрузки) равен примерно 0.15. Во-вторых, входящий поток запросов системы хранения представляет собой сумму большого числа потоков, и на основании предельной теоремы о сумме потоков, он сходится к простейшему. Важно, что время вычисления в кластере является случайной величиной, с функцией распределения отличной от экспоненты. Поскольку время обсчета одного блока исходных данных представляет собой сумму времен обсчета большого числа случайных данных (трасс), то по предельной теореме о распределении суммы независимых случайных величин, распределение этой случайно величины стремится к нормальному, квадратичный коэффициент вариации которого меньше единицы. Таким образом, суммарный поток представляет собой сумму случайных потоков с коэффициентами вариации меньше единицы, то есть сходится к простейшему потоку снизу, следовательно, , оставаясь меньше единицы. Обобщив два этих утверждения, получим: .

С учетом вышеописанных допущений целевая функция (2) примет вид:

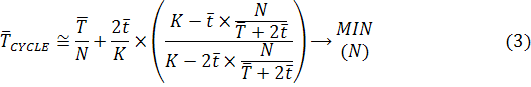
Вычислив производную функции (3) составим уравнение: , решив которое относительно N получим выражение для оптимального числа вычислительных узлов:

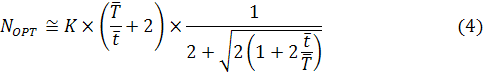
Если учесть, что для рассматриваемого класса задач T много больше t и имеет достаточно большой порядок, то выражение (4) можно упростить: .

Полученное соотношение позволяет легко определить оптимальное число вычислительных узлов кластера при заданных параметрах системы хранения и известных временных характеристиках оборудования комплекса. Покажем теперь, как можно определить оптимальную конфигурацию комплекса не имея в наличии данных временных характеристик.

В формуле (4) присутствуют параметры (средние значения времени обслуживания T и t), для нахождения которых необходимо связать параметры математической модели с характеристиками кластера и дисковой системы. Характеристики оборудования могут быть получены по результатам стандартных промышленных тестов производительности. Для вычислительных кластеров – это тест HPL из набора тестов HPC Challenge benchmark [9], для систем хранения данных – тест LFP из тестового пакета Storage Performance Council 2 benchmark [10]. Стандартные тесты применяются для оценки параметров производительности множества промышленных систем (их результаты доступны и постоянно публикуются); выбор этого способа получения исходных данных оправдан и хорош тем, что позволяет в дальнейшем проводить исследования любых систем.

Тест HPL – highly parallel linpack. Именно по его результатам дважды в год формируется список из 500 самых производительных суперкомпьютеров в мире [11]. В тесте HPL оценивается средняя (рабочая) и максимальная (пиковая) производительность системы при выполнении вычислений с плавающей точкой. Ее величина измеряется во FLOP/s (floating point operations by second – операциях с плавающей точкой в секунду). Обычно производительность оценивается в расчете на одно ядро, что связано с особенностью масштабирования кластерных систем.

Тест LFP – large file processing. Оценивает параметры производительности системы хранения данных при работе с большими файлами. В процессе тестирования отдельно измеряется скорость чтения данных, скорость записи данных и скорость случайных операций чтения-записи. Результаты определяются для случаев работы с блоками данных различной длины. Скорость чтения (записи) измеряется в MB/s. Помимо собственно результатов теста в отчете всегда указывается число виртуальных томов, задействованных в процессе тестирования, что дает возможность представить результат в расчете на один том.

Покажем теперь, как связаны параметры модели с характеристиками оборудования:

Среднее время обслуживания заявки в ВК:

где L – производительность ВК (по тесту HPCC HPL, FLOP/s),

V – объем обрабатываемых данных.

Параметр Q – удельная трудоемкость решения задачи, определяющая, какое количество операций с плавающей точкой приходится на один байт обрабатываемой информации. Именно параметр Q определяет специфику решаемой задачи (специфику алгоритма решаемой задачи), то есть каждому классу задач (и каждому методу их решения) будет соответствовать свое значение удельной трудоемкости.

Среднее время обслуживания заявки в СХД:

где S – пропускная способность СХД (по тесту SPC-2 LFP, MB/s),

V – объем обрабатываемых данных.

Если подставить в формулу (4) соотношения (5) и (6), то можно получить выражение для зависимости оптимального числа процессорных ядер кластера от количества томов системы хранения и результатов стандартных тестов производительности:

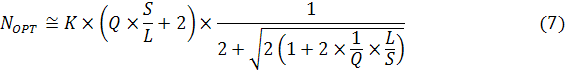
Или в упрошенном варианте:

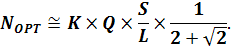
Формула (7) позволяет легко определять оптимальную конфигурацию вычислительного комплекса по характеристикам, полученным из результатов стандартных промышленных тестов производительности для вычислительных кластеров и систем хранения данных.

Литература

1. Суперкомпьютерные технологии в науке, образовании и промышленности (первый выпуск) / под редакцией: академика В.А.Садовничего, академика Г.И.Савина, чл.-корр. РАН Вл.В.Воеводина. – М.: Издательство Московского университета, 2009. – 232с.

2. Суперкомпьютерные технологии в науке, образовании и промышленности (второй выпуск) / под редакцией: академика В.А.Садовничего, академика Г.И.Савина, чл.-корр. РАН Вл.В.Воеводина. – М.: Издательство Московского университета, 2010. – 208с.

3. M.McDade. Sun C48 & Lustre fast for Seismic Reverse Time Migration using Sun X6275, 2009.

4. R.T.Mills, V.Sripathi, G.Mahinthakumar, G.E.Hammond, P.C.Lichtner, B.F.Smith. Engineering for Scalable Performance on Cray XT and IBM BlueGene Architectures, 2010.

5. М.А.Файнберг. Об одной приближенной формуле в теории массового обслуживания. Известия АН СССР. Техническая кибернетика. 1974, №5.

6. В.А.Мясников, Ю.Н.Мельников, Л.И.Абросимов. Методы автоматизированного проектирования систем телеобработки данных. Учебное пособие для вузов. – М.: Энергоатомиздат, 1992. – 299с.

7. Л.И.Абросимов. Анализ и проектирование вычислительных сетей. Учебное пособие. – М.: Издательство МЭИ, 2000. – 52с.

8. Edward Kihyen Lee. Performance Modeling and Analysis of Disk Arrays. University of California at Berkeley, 1993.

9. HPC Challenge Benchmark. [25.05.2011]

http://icl.cs.utk.edu/hpcc/

10. SPC Benchmark. [25.05.2011]

http://www.storageperformance.org/home/

11. TOP500 Supercomputer Sites. [25.05.2011]

http://www.top500.org/