Расчет структуры вычислительной

сети иерархической древовидной конфигурации

Абросимов Л.И.

6

1

7

2 5

9

4

3 8

Рис. 1

Даны узлы, расположенные как показано выше на рис. 1 , заданы взвешенные расстояния, представленные в матрице М на рис. 2.

	1	2	3	4	5	6	7	8	9
1	0	10	24	21	45	65	60	55	100
2	10	0	15	11	35	55	50	48	90
3	24	15	0	25	50	70	75	60	100
4	21	11	25	0	25	45	40	35	60
5	45	35	50	25	0	40	30	26	70
6	65	55	70	45	40	0	12	30	40
7	60	50	75	40	30	12	0	18	28
8	55	48	60	35	26	30	18	0	40
9	100	90	100	60	70	40	28	40	0

Рис. 2

Задано, что вес каждого узла равен 1.

Суммарный вес центра группы уровня h=2 равен 3, следовательно, каждая группа должна состоять из 3-х узлов нижнего уровня. Суммарный вес центра группы уровня h=3 равен 9.

Требуется построить древовидную иерархическую сеть минимальной длины, обеспечивающую многоуровневое покрытие исходных узлов. Например, так, как показано на рис.3.

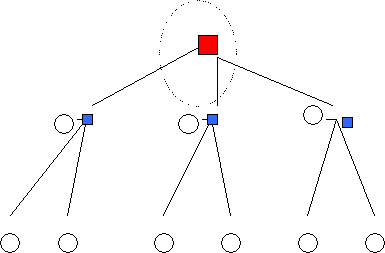
Уровень h=3

Уровень h=2

Уровень h=1

Рис. 3

На рис. 3 показано, что при некоторых узлах, являющихся центрами групп, располагаются местные вычислительные центры (это могут быть и концентраторы) – квадраты синего цвета. Красный квадрат – это главный информационно – вычислительный центр.

Итак, исходные данные для расчета следующие:

N=9; количество узлов

z_i=1; веса узлов, которые равны количеству информации, передаваемой узлом за единицу времени

П_h=1=3; пропускные способности центров групп h=1

П_h=2=9, пропускные способности центров групп h=2.

Алгоритм решения состоит из двух этапов:

· определение группы (центр, состав, число элементов)

· улучшение группы путём обмена наиболее удалённых её элементов с элементами соседних групп

Решение:

Определение группы

1) Производим преобразование исходной матрицы М и из исходной матрицы получаем три: _, M^K, M^C.

Упорядоченная матрица (каждый столбец исходной матрицы упорядочивается по возрастанию) представлена на рис. 4

	1	2	3	4	5	6	7	8	9
1	0	0	0	0	0	0	0	0	0
2	10	10	15	11	25	12	12	18	28
3	21	11	24	21	26	30	18	26	40
4	24	15	25	25	30	40	28	30	40
5	45	35	50	25	35	40	30	35	60
6	55	48	60	35	40	45	40	40	70
7	60	50	70	40	45	55	50	48	90
8	65	55	75	45	50	65	60	55	100
9	100	90	100	60	70	70	75	60	100

Рис. 4

Матрица номеров M^K, в нее записываются порядковые номера переставленных элементов, представлена на рис. 5

	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	1	2	2	4	7	6	7	7
3	4	4	1	1	8	8	8	5	6
4	3	3	4	3	7	5	9	6	8
5	5	5	5	5	2	9	5	4	4
6	8	8	8	8	6	4	4	9	5
7	7	7	6	7	1	2	2	2	2
8	6	6	7	6	3	1	1	1	1
9	9	9	9	9	9	3	3	3	3

Рис. 5

Матрица суммарная M^C, получается путем последовательного суммирования элементов столбца упорядоченной матрицы, представлена на рис 6

Матрица суммарная M^C

	1	2	3	4	5	6	7	8	9
1	0	0	0	0	0	0	0	0	0
2	10	10	15	11	25	12	12	18	28
3	31	21	39	32	51	42	30	44	68
4	55	36	64	57	81	82	58	74	108
5	100	71	114	82	116	122	88	109	168
6	155	119	174	117	156	167	128	149	238
7	215	169	244	157	201	222	178	197	328
8	280	224	319	202	251	287	238	252	428
9	380	314	419	262	321	357	313	312	528

Рис. 6

2. Находим состав группы.

Просматриваем очередную строку i суммарной матрицы М^С и ищем минимальный элемент j. Принимаем, что при этом элементе j располагается центр группы, состоящей (разумеется) из i узлов.

Проверяем ограничение по пропускной способности: åz_i £ П_{h=1 или 2} (для соответствующего уровня h). Если ограничение выполняется, то увеличиваем номер строки i=i+1 и всё повторяем сначала. В противном случае оставляем состав группы с предыдущего шага(i-1).

В нашем примере задано найти три узла, входящие в группу. Поэтому дойдем до 3-й строки матрицы М^С (z_i=1, а П_h=1=3), в этой строке минимальным является элемент m₃₂=21.

Центр группы располагается при 2-м узле (j=2). Всего в группе три узла (i=3). По столбцу 2 матрицы номеров М^К определяем номера узлов, входящих в группу Г₁=2,1,4.

Корректировка для первой группы не производится

3. Вычёркиваем строки и столбцы из исходной матрицы М с номерами элементов, входящих в группу. В данном случае это строки 1,2,4 и столбцы 1,2,4. Получаем матрицу М⁽¹⁾, представленную на рис 7

	3	5	6	7	8	9
3	0	50	70	75	60	100
5	50	0	40	30	26	70
6	70	40	0	12	30	40
7	75	30	12	0	18	28
8	60	26	30	18	0	40
9	100	70	40	28	40	0

Рис. 7

4. Если число групп > 1, переходим к следующему этапу (улучшение группы), иначе к шагу 1.

В рассматриваемом примере имеем одну группу и опять из исходной матрицы М⁽¹⁾ формируем три: , М^К(1), М^С(1)

Матрица упорядоченная Матрица М^С(1) суммарная

	3	5	6	7	8	9		3	5	6	7	8	9
3	0	0	0	0	0	0	3	0	0	0	0	0	0
5	50	26	12	12	18	28	5	50	26	12	12	18	28
6	60	30	30	18	26	40	6	110	56	42	30	44	68
7	70	40	40	28	30	40	7	180	96	82	58	74	108
8	75	50	40	30	40	70	8	255	146	122	88	114	178
9	100	70	70	75	60	100	9	355	216	192	163	174	278

Рис. 8 Рис. 9

Матрица М^К(1) номеров

	3	5	6	7	8	9
3	3	5	6	7	8	9
5	5	8	7	6	7	7
6	8	7	8	8	5	6
7	6	6	5	9	6	8
8	7	3	9	5	9	5
9	9	9	3	3	3	3

Рис. 10

Далее согласно п. 2 определяем группу. Минимальный элемент m₆₇=30. Следовательно, центр группы при 7-м узле, а состав группы Г₂=7,6,8.

5. Проверяем необходимость корректировки группы Г₂=7,6,8

Центр улучшаемой группы Г_у = Г₂ расположен при узле 7. Узлы 6,8 должны корректироваться, если расстояние от корректируемого узла до центра улучшаемой группы Г_у больше расстояния от корректируемого узла до центра группы Г₁ при узле 2, из которой может выделяться узел, который участвует в корректировке, т.е. в рассматриваемом примере для корректируемых узлов 6 и 8 должны соответственно выполняться условия: m₈₇ > m₈₂ либо m₆₇ > m₆₂

По матрице номеров М^К, представленной на рис. 5, анализируем соответственно столбцы 8 и 6, как представлено на рис 11.

	6	8
1	6	8
2	7	7
3	8	5
4	5	6
5	9	4
6	4	9
7	2	2
8	1	1
9	3	3

Рис. 11

В каждом из этих столбцов узлы 6 и 8находятся выше узла 2. Это означает, что центр Г₂ при узле 7 расположен к рассматриваемым узлам 6 и 8 ближе, чем центр Г₁ , расположенный при узле 2.

Поэтому корректировку Г₂ производить не следует.

6. Находим следующую группу.

После вычёркивания из матрицы М⁽¹⁾ строк и столбцов, номера которых соответствуют номерам узлов, входящих в Г₂, получаем матрицу М⁽²⁾, представленную на рис.12.

	3	5	9
3	0	50	100
5	50	0	70
9	100	70	0

Рис. 12

Как обычно, формируем три матрицы , М^К(2), М^С(2)

Упорядоченная Номеров М^К(2), Суммарная М^С(2)

	3	5	9		3	5	9		3	5	9
3	0	0	0	3	3	5	9	3	0	0	0
5	50	50	70	5	5	3	5	5	50	50	70
9	100	70	100	9	9	9	3	9	150	120	170

. Рис. 13 Рис. 14 Рис. 15

Минимальный элемент m₉₅=120. Центр группы при 5-м узле, состав группы Г₃=5,3,9.

7. Улучшение группы Г₃

Центр улучшаемой группы Г_у = Г₃ расположен при узле 5. Узлы 3,9 могут корректироваться, если расстояние m₃₅ > m₃₂ либо m₉₅ > m₉₇ .

По матрице номеров М^К, представленной на рис. 5, анализируем соответственно столбцы 3 и 9, которые приведены на рис.16.

В 3-м столбце узел 2 находятся выше узла 5. Это означает, что центр Г₁ при узле 2 расположен к улучшаемому узлу 3 ближе, чем центр Г₃, расположенный при узле 5. Поэтому корректировку узла 3 следует производить.

В 9-м столбце узел 7 находятся выше узла 5. Это означает, что центр Г₂ при узле 7 расположен к улучшаемому узлу 9 ближе, чем центр Г₃, расположенный при узле 5. Поэтому корректировку узла 9 также следует производить.

	3	9
1	3	9
2	2	7
3	1	6
4	4	8
5	5	4
6	8	5
7	6	2
8	7	1
9	9	3

Рис. 16

В процессе корректировки узел 3 из группы Г₃ необходимо передать в группу Г₁ (с центром

в узле 2), а из группы Г₁ необходимо узел, ближайший к группе Г₃ (с центром в узле 5), включить в состав группы Г₃.

Группа Г₁ имеет для корректировки два узла –1 и 4. Чтобы найти, который из этих узлов расположен ближе к центру 5 группы Г₃, рассмотрим матрицу номеров М^К, представленную на рис. 5, точнее ее 5-й столбец, приведенный на рис. 17. В этом столбце узел 4 расположен выше узла 2, следовательно, необходимо узел 3 включить в состав Г₁, а узел 4 – в состав Г₃.

	5
1	5
2	4
3	8
4	7
5	2
6	6
7	1
8	3
9	9

Рис. 17

Кроме того, в процессе корректировки узел 9 из группы Г₃ необходимо передать в группу Г₂ (с центром в узле 7), а из группы Г₂ необходимо узел, ближайший к группе Г₃ (с центром в узле 5), включить в состав группы Г₃.

Группа Г₂ имеет для корректировки два узла –6 и 8. Чтобы найти, который из этих узлов расположен ближе к центру 5 группы Г₃, рассмотрим 5-й столбец матрицы номеров М^К, приведенный на рис. 17. В этом столбце узел 8 расположен выше узла 7, следовательно, необходимо узел 8 включить в состав Г₃, а узел 4 – в состав Г₃.

Таким образом, получаем скорректированные группы первого уровня:

Г₁ = 2,1,3; Г₂ = 7,6,9; Г₃ = 5,4,8.

8. В рассматриваемом примере вес каждого узла равен 1, а пропускные способности центров групп П_h=1=3. Для каждой из полученных групп выполняется условие равенства пропускных способностей, поэтому корректировка завершена.

Определение групп следующего уровня

9. Все узлы уровня h =1 сгруппированы, переходим к определению групп уровня h = 2.

Исходными узлами для уровня h = 2 являются центры групп уровня h =1, которые расположены при узлах 2,7,5.

1. Корректируем исходную матрицу М так, что в ней остаются только центры групп

	2	5	7
2	0	35	50
5	35	0	30
7	50	30	0

Рис. 18

2. Как обычно формируются три матрицы

Упорядоченная Номеров Суммарная

	2	5	7		2	5	7		2	5	7
2	0	0	0	2	2	5	7	2	0	0	0
5	35	30	30	5	5	7	5	5	35	30	30
7	50	35	50	7	7	2	2	7	85	65	80

Рис. 19 Рис. 20 Рис. 21

Минимальный элемент m₇₅=65. Центр группы при 5-м узле, состав группы Г₁=5,7,2.

Так как сформирована только одна группа, то процедура расчёта заканчивается.

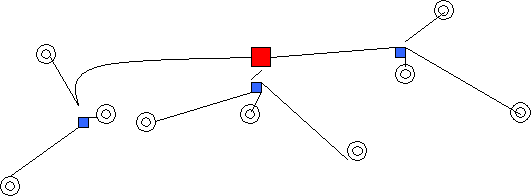Результат расчета структуры представлен на рис. 22

6

1

7

2 5

9

4

8

3

Рис. 22