оценка параметров вычислительных комплексов для решения задач обработки больших объемов данных по результатам стандартных тестов производительности
Ю.Н. Домаров, В.О. Рыбинцев
В работе [1] была
предложена математическая модель вычислительного комплекса для решения задач
высокопроизводительной обработки больших объемов информации,приведено
соотношение, описывающее зависимость оптимального числа вычислительных ядер от
времени обслуживания заявки в кластере (
) и дисковой системе (
):
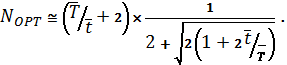(1)
Однако, в формуле (1)
присутствуют параметры (средние значения времени обслуживания
и 
), для нахождения которых необходимо связать параметры
математической модели с характеристиками кластера и дисковой системы, которые
могут быть получены по результатам стандартных промышленных тестов: для
вычислительных кластеров – это набор тестов HPCC [2], для систем
хранения данных – SPC-2[3]. Покажем, как связаны параметры
модели с характеристиками оборудования:
(2)
где V – объем данных;L – производительность
кластера по тесту HPCCHPL (на ядро, FLOP/s);S – пропускная
способность системы хранения по тесту SPC-2 LFP
(на том, MB/s);Q
– удельная трудоемкость решения задачи, определяет специфику решаемой задачи
(алгоритма).
Подставив соотношения
(2) в выражение (1) получим:
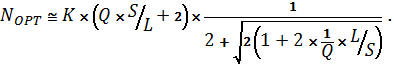(3)
Формула (3) позволяет определять
оптимальную конфигурацию вычислительного комплексапо характеристикам,
полученным из результатов стандартных промышленных тестов производительности
для вычислительных кластеров и систем хранения данных.
Литература
1.В.О. Рыбинцев, Ю.Н. ДомаровМатематическая
модель вычислительного комплекса для решения задач высокопроизводительной
обработки больших объемов информации: тр. XIX МНТК «Информационные средства и технологии» М.: МЭИ,
2011.
2.HPCCChallengeBenchmark. [15.10.2011]
3. SPC Benchmark. [15.10.2011]