СТРУКТУРНАЯ ИНФОРМАТИКА: ТРАНСГРАФЫ ПОЛУПУТЕЙ ДЛЯ ОРДЕРЕВЬЕВ
И ИХ СВОЙСТВА
В.В. Кохов, В.Н.Фальк
Разработка эффективных
алгоритмов определения сложности и сходства графовых моделей систем (ГМС)
актуальна для создания новых поколений: (1) информационно-поисковых систем
структурной информации (семантический web-поиск документов); (2) систем искусственного
интеллекта с правдоподобными рассуждениями.
В докладе предложена
система эффективных методов для построения нового класса моделей – трансграфов полупутей. Методы
предназначены для более точного анализа сложности и сходства ордеревьев. Предложенные модели расширяют функциональные
возможности ПСУН, используемого при обучении студентов АВТИ [1,2].
Применение трансграфов
полупутей позволило создать два более точных подхода к анализу сходства
ордеревьев на основе: (1) вычисления и учета вклада каждого полупути в общую
сложность ордерева; (2) расширения возможностей поструктурно-метрического
подхода, учитывающего не только расположение путей, но и полупутей в ордереве.
Кроме того, построение трансграфов полупутей позволяет: (1) визуализировать
каждый полупуть вершиной трансграфа полупутей ghp(dt) ордерева dt; (2) исследовать все
группы автоморфного расположения полупутейhpвсех типов как одну группу автоморфизмов вершин ghp(dt); (3) для каждого
ордерева dt на основе единой
методики решать задачи построения семейств неизоморфных орграфов с изоморфными
группами; (4) внедрять новые информационные технологии в обучение студентов
университетов при изучении графовых моделей систем, их сходства и сложности
[1].
На рис. 1 приведены
три ордерева (dt1=(V1,E1), dt2=(V2,E2), dt3=(V3,E3)) и их трансграфы
полупутей (ghp(dt1),ghp(dt2),ghp(dt3)).
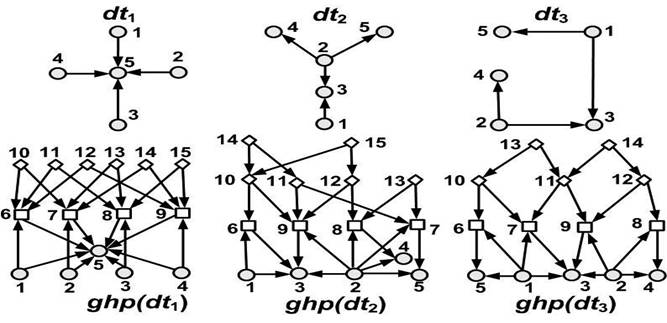
Рис. 1. Примеры трансграфов полупутей для ордеревьев
Вершины, соответствующие
путям ордерева длиной больше нуля обозначены квадратами, а полупутям –
ромбами.В докладе выделены три основных свойства трансграфов полупутей для
ордеревьев: (1) каждому полупути взаимнооднозначно соответствует вершина в
трансграфе полупутей; (2) для любого ордерева группа автоморфизмов вершин
ордерева изоморфна группе автоморфизмов вершин трансграфа полупутей; (3)
группа, характеризующая расположение полупутей в ордереве, изоморфна группе
автоморфизмов вершин в трансграфе полупутей. Заметим, что в общем случае пути
ордерева являются частным случаем его полупутей.
Пусть gp(dt) обозначает трансграф путей ордерева dt, а MCS(dti,dtj) - максимальный общий
подграф ордеревьв dti
и dtj. В таблице приведены
результаты определения попарных расстояний (D1, D2, D3), полученные при
анализе сходства трех анализируемых ордеревьев на основе
структурно-метрического подхода, где
D1(dti,dtj)=÷V(dti)ç+÷V(dtj)ç-2÷V(MCS(dti,dtj))ç;
D2(gp(dti,dtj))=÷V(gp(dti))ç+÷V(gp(dtj))ç-2÷V(MCS(gp(dti),gp(dtj))ç;
D3(dti,dtj)=÷V(ghp(dti))ç+÷V(ghp(dtj))ç-2÷V(MCS(ghp(dti),ghp(dtj))ç.
Таблица
|
|
dt1 |
dt2 |
dt3 |
gp(dt1) |
gp(dt2) |
gp(dt3) |
ghp(dt1) |
ghp(dt2) |
ghp(dt3) |
|
dt1 |
0 |
4 |
4 |
4 |
8 |
8 |
4 |
14 |
13 |
|
dt2 |
4 |
0 |
2 |
8 |
4 |
6 |
8 |
10 |
11 |
|
dt3 |
4 |
2 |
0 |
8 |
6 |
4 |
8 |
12 |
9 |
|
gp(dt1) |
4 |
8 |
8 |
0 |
8 |
8 |
0 |
14 |
13 |
|
gp(dt2) |
8 |
4 |
6 |
8 |
0 |
4 |
8 |
6 |
9 |
|
gp(dt3) |
8 |
6 |
4 |
8 |
4 |
0 |
8 |
10 |
5 |
|
ghp(dt1) |
4 |
8 |
8 |
0 |
8 |
8 |
0 |
14 |
13 |
|
ghp(dt2) |
14 |
10 |
12 |
14 |
6 |
10 |
14 |
0 |
7 |
|
ghp(dt3) |
13 |
11 |
9 |
13 |
9 |
5 |
13 |
7 |
0 |
Анализ результатов,
приведенных в таблице, показывает, что на основе трансграфов полупутей получаем
более точную информацию о сходстве ордеревьев, чем на основе трансграфов путей.
В докладе подробно
рассмотрен новый метод анализа сходства ордеревьев на основе вычисления
значений вкладов полупутей в общую сложность ордеревьев.
Литература
1. Кохов В.А., Джасим М.Р.,
Кохов В.В. Интегрированная среда визуального и алгоритмического решения
задач поиска, сравнительного анализа и определения сложности ациклических
графовых моделей систем. // ПСУН. Паспорт от 18.06.2009 г. – М., МЭИ,
2009.
2. Кохов В.В., Фальк В.Н.
Структурная информатика: трансграфы деревьев, ордеревьев и их свойства : Тр.
17-ой международной НТК. М.: МЭИ, 2011. Т1. С. 372-373.