BC/NW 2012; №2 (21):.10.3

ОПТИМИЗАЦИЯ КОНФИГУРАЦИИ ОКНА СКАНИРОВАНИЯ В ФРАГМЕНТАРНОМ МЕТОДЕ СЖАТИЯ ВИДЕОПОТОКА БЕЗ ПОТЕРЬ

Огнев И.В., Огнев А.И., Горьков А.Г.

В статье "Алгоритм формирования базы данных для фрагментарного метода сжатия видеопотока без потерь" был предложен метод сжатия видеопотока без потерь, основанный на получении т.н. базы данных элементов. Но в статье был описан только алгоритм формирования базы данных, в то время, как важнейший вопрос оптимизации окна сканирования рассмотрен не был.

Коэффициент сжатия

Напомним основные шаги алгоритма сжатия видеопотока без потерь:

1. Создание базы элементов. На этом этапе для всех окон вычисляются элементы, реально встречающихся в видеопотоке.

2. Построение коротких кодов для элементов. Для получения кодов строится кодовое дерево;

3. Кодирование фильма. Для каждого окна соответствующий элемент кодируется полученным на 2 шаге коротким кодом.

Чтобы понять, от чего зависит эффективность сжатия, необходимо рассмотреть структуру сжатого фильма. Она приведена на Рис. 1

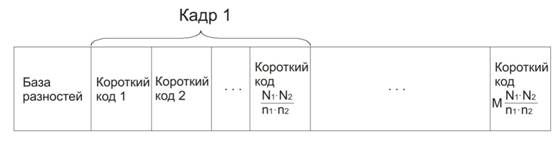
Рис. 1. Структура сжатого фильма

Эффективностью (коэффициентом) сжатия () будем называть отношения объёмов исходного фильма к сжатому фильму.

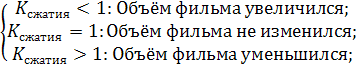
Чтобы сжатие было эффективным, необходимо, чтобы , причём, чем больше, тем эффективнее сжатие.

Объём исходного фильма фиксирован и равен , где - высота кадра, - ширина кадра, - количество кадров в фильме, - количество бит на пиксель.

Объём сжатого фильма оценить немного сложнее. Этот объём складывается из двух составляющих:

· База данных элементов;

· Короткие коды.

Кодовое дерево базы данных

В статье " Алгоритм формирования базы данных для фрагментарного метода сжатия видеопотока без потерь" было предложено для передачи базы передавать элемент и его частоту (или количество появлений). Т.е. для передачи базы нам бы потребовалось передать бит, где - количество реально встретившихся элементов. Получается, что на каждый элемент мы бы передавали лишние 64 бита.

Объём передачи можно значительно уменьшить, если передавать не саму базу, а построенное на её основе кодовое дерево. Кодовое дерево - это несбалансированное двоичное дерево. Листья этого дерева хранят элементы базы данных.

Т.к. дерево не сбалансировано, то мы не можем передавать его в виде классической двоичной кучи[1][2], но мы можем прибегнуть к другому способу. Договоримся о порядке обхода дерева, например, будем использовать обход в ширину. Если мы встречаем узел дерева, то передаём бит , если в процессе обхода мы дошли до листа, то передаём бит и соответствующий элемент базы. Т.к. размер элемента в битах нам известен (он зависит от ), то никакой вспомогательный заголовок нам не нужен. В итоге на каждый элемент базы мы передаём всего 2 лишних бита. На Рис. 2 показано представление двоичного дерева в виде двоичной строки с помощью описанного метода:

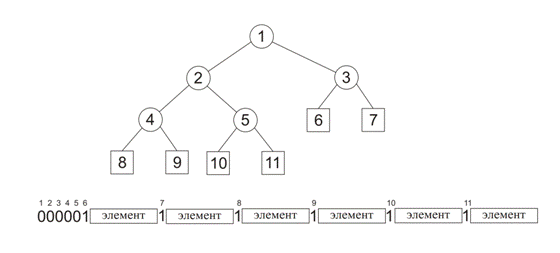
Рис. 2. Эффективное кодирование двоичного дерева

Указанное представление обратимо: т.е. для каждой строки, построенной описанной способом, можно построить исходное кодовое дерево.

При описанном способе кодирования объём передачи значительно сокращается. На Графике 1 показано отношение объёмов передач при :

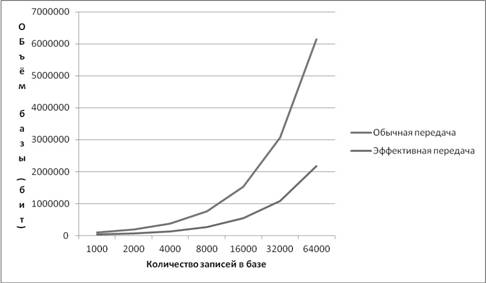
График 1. Объёмы базы при различных способах передачи

Помимо очевидной экономии памяти, описанный способ передачи избавляет от необходимости строить кодовое дерево при декодировании. Т.е. кодовое дерево строится только один раз во время сжатия.

Вычисление коэффициента сжатия

При передаче закодированного фильма вместо реальных элементов базы передаются их короткие коды. Для полного восстановления фильма в передаче должны содержаться короткие коды всех элементов базы, т.е. их количество известно и равно , но длина коротких кодов нам заранее не известна.

Хоть нам и не известна реальная длина коротких кодов, но мы можем весьма точно её оценить. В качестве оценки воспользуемся энтропией базы элементов: . Хоть энтропия и является оценкой "снизу", но эксперименты показывают, что такая оценка весьма точна, и разница появляется только в 3 знаке после запятой.

Учитывая всё вышеописанное, можно привести окончательную формулу для коэффициента сжатия:

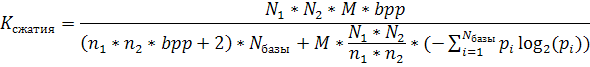
Оптимизация конфигурации окна сканирования

Основная цель, которой мы хотим достигнуть, - максимизация . В формуле, приведённой выше, - константы, на которые мы влиять не можем. - величины, зависящие от . На самом деле, единственные вариабельные параметры - это , но их влияние на остальные элементы формулы практически невозможно выразить аналитически.

Для начала мы рассмотрим влияние величины на коэффициент сжатия. Для любого размера окна существует максимально возможный объём базы, равный , и эта величина растёт чрезвычайно быстро (см. таблицу 1):

Таблица 1 Максимальный размер базы данных

	Мак.
1	16
2	256
3	4096
4	65536
5	1048576
6	16777216
7	268435456
8	4294967296
9	68719476736
10	1099511627776

Конечно, в реальных фильмах встречаются далеко не все возможные элементы, но с увеличением размера окна, растёт и количество бит, необходимое для представления соответствующего элемента базы. Кроме того, появляется огромное количество (более 70% от общего числа) элементов, которые встречаются в видеопотоке 1 раз. В конечном итоге всё это приводит к уменьшению коэффициента сжатия.

С другой стороны слишком маленький размер окна приведёт к тому, что увеличится количество элементов, которые необходимо передать, элементы будут повторяться более равномерно и "перекос" частот сгладится. Чем равномернее повторяются элементы базы, тем ближе энтропия к . Это в свою очередь тоже приводит к уменьшению коэффициента сжатия.

Рассмотрим два крайних случая окно и окно . В первом и во втором случае . В процессе исследований было установлено, что график функции ) имеет примерно следующий вид (см. График 2):

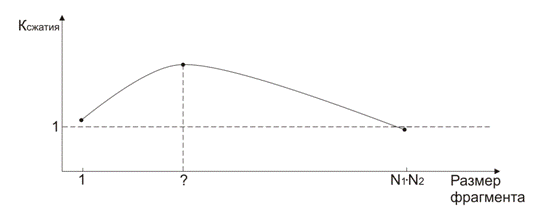
График 2. Зависимость коэффициента сжатия от размера окна сканирования

Задача заключается в том, чтобы найти точку, где уровень сжатия максимальный. Т.к. уровень сжатия во многом зависит и от характеристик фильма, понятно, что не существует "идеальной" конфигурации, которая будет давать оптимальное сжатие для всех фильмов. Но эксперименты позволили найти небольшую область, где сжатие оптимально.

В ходе экспериментов было обработано несколько типов видеофильмов:

· Студийные съёмки (однородный фон);

· Видовые съёмки (разнообразный часто меняющийся фон);

· Мультфильмы.

Каждый из фильмов был обработан всеми возможными конфигурациями окна размером от 2 до 10 пикселов.

На графиках 3,4,5 приведены результаты экспериментов с базой данных, где элементами являются разности фрагментов. Заливкой выделены наилучшие конфигурации в пределах заданного размера:

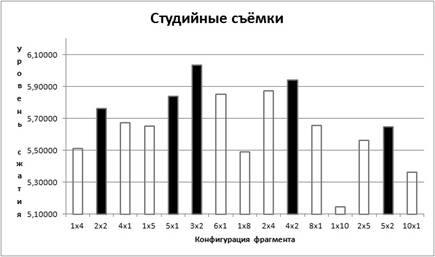
График 3. Уровень сжатия (студийные съёмки)

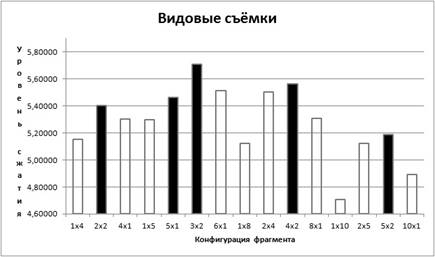
График 4. Уровень сжатия (съёмки на природе)

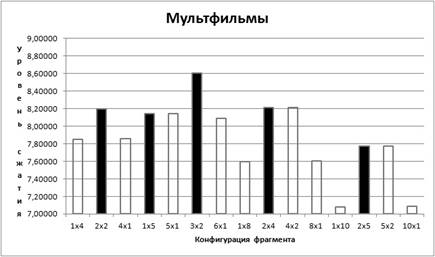
График 5. Уровень сжатия (мультфильмы)

Из графиков видно, что лучше всего сжимаются мультфильмы (8,6 раз), на втором месте студийные съёмки (6 раз), и на третьем месте видовые съёмки (5,7 раз).

Для всех трёх типов видеопотока максимум сжатия наблюдается для конфигурации окна . Кроме того, наблюдается интересный эффект. Если размер окна фиксирован, то эффективность сжатия падает (для мультфилтмов эффективность сжатия практически не меняется) при смене конфигураций в следующем порядке:

· Прямоугольник (вытянутый по высоте)

· Прямоугольник (вытянутый по ширине)

· Столбец

· Строка

Это можно объяснить особенностями реального видео: многие объекты (люди, деревья, дома) вытянуты по высоте и поэтому лучше укладываются в окна подобной формы.

Заключение

В статье предложены и проанализированы методики оценки уровня сжатия и оптимизации конфигурация окна сканирования. Выбран оптимальный размер окна и оптимальная конфигурация окна. Всё это позволяет значительно улучшить общую эффективность предлагаемого алгоритма.

Литература

1. Ахо А.В., Хопкрофт Д.Э., Ульман Д.Д., Структуры данных и алгоритмы, -М.: Издательский дом "Вильямс", 2010. -400с: ил.

2. Скиена С., Алгоритмы. Руководство по разработке., -СПб.: БХВ-Петербург, 2011. - 720 с.: ил.

3. Вирт Н., Алгоритмы и структуры данных. Новая версия для Оберона +CD. -М.: ДМК Пресс, 2010. -272 с.: ил.