BC/NW 2012; №2 (21):5.1

РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ ОПРЕДЕЛЕНИЯ ПРОИЗВОДИТЕЛЬНОСТИ ПРОКСИ-СЕРВЕРА

Абросимов Л.И., Крамаренко М.Д.

В современном мире сетевые технологии находят применение в практически каждой сфере науки и техники. Сетевые технологии постоянно развиваются, появляются все новые технологии и сервисы и для повышения качества обслуживания пользователей требуется решение задачи определения производительности серверов по обработке сетевого трафика.

В настоящее время основные методы определения производительности серверов по обработке сетевого трафика рассматривают серверы как «черный ящик», что не позволяет учесть особенности задач, которые решает сервер при обработке сетевого трафика, а так же вариативность аппаратного и программного обеспечения. Отсутствие дифференцированного подхода к решению сетевых задач влияет на точность оценки при проектировании производительности сервера по обработке сетевого трафика. Для повышения точности расчета производительности серверов необходимо использование математической модели сервера, основанной на теории СМО и устраняющей недостатки модели «черного ящика».

В данной статье излагаются результаты разработки математической модели сервера, позволяющей определить производительность сервера, учитывающую специфику обработки сетевого трафика и особенности программного и аппаратного обеспечение сервера.

Для создания математической модели сервера, для определения производительности обработки сетевого трафика необходимо:

o конкретизировать объект исследования;

o исследовать особенности функционирования объекта;

o определить исходные данные;

o рассмотреть существующие модели;

o составить математическое описание модели.

Исследуемым объектом является сервер, который рассматривается как однопроцессорная ЭВМ, функционирующая под управлением ОС, например, Linux, c установленным программным обеспечением, которое позволяет однопроцессорной ЭВМ работать в качестве прокси-сервера IP-телефонии. Однопроцессорная ЭВМ удобна для проведения исследований, поскольку гарантированно весь алгоритм функционирования прокси-сервера и все алгоритмы ОС, необходимые для этого функционирования, будут исполнены на данном процессоре.

В качестве операционной системы прокси-сервера была выбрана ОС Linux, поскольку:

o ОС Linux широко применяется и является типичной ОС, обладающей всеми типичными механизмами ОС;

o ОС Linux предлагает широкий спектр прикладного и системного ПО;

o ОС Linux обладает открытым исходным кодом, что делает её чрезвычайно удобной для исследований ОС.

Прокси-сервер IP-телефонии обладает рядом особенностей функционирования:

o использование прокси-серверов в IP-телефонии является базовым решением, что в свою очередь дает возможность проводить эксперименты на реальном трафике сети;

o прокси-сервер выполняет как прием, так и отправку требований, что дает возможность исследовать механизмы обработки, как входящих, так и исходящих требований ОС прокси-сервера;

Для устранения недостатков модели «черного ящика» рассмотрим механизм функционирования прокси-сервера. Поскольку, прокси-сервер является ЭВМ, управляемой ОС Linux, то обработка сетевых требований происходит в соответствии с моделью ЭМВОС.

В данной статье исследуются оценки производительности прокси-сервера на сетевом и транспортном уровнях модели ЭМВОС. С таким подходом солидарен и Э. Таненбаум, который в [1] утверждает, что основные задержки при функционировании компьютерных сетей возникают именно на транспортном уровне, при этом сетевой уровень так же вносит свою задержку.

Следует подчеркнуть, что сетевой и транспортный уровни модели ЭМВОС в ОС Linux реализованы в виде программных функций ядра ОС Linux, поэтому производительность обработки сетевого трафика будет определяться временем выполнения данных функций. В связи с тем, что программные функции ядра ОС могут содержать операции ветвления, а также циклы, [2] то времена выполнения одной и той же функции могут различаться. Для учета отмеченных особенностей функционирования прокси-сервера применяется аппарат теории вероятностей и в качестве оценок используется математическое ожидание времени выполнения функции, которое определяет вероятностно-временные характеристики прокси-сервера.

Для измерения вероятностно-временных характеристик прокси-сервера по обработке сетевого трафика можно воспользоваться программой-трассировщиком, поскольку использование данного типа программ позволяет зафиксировать вызовы программных функций. Для измерений была выбрана программа SystemTap, которая имеет ряд преимуществ и позволяет:

o установить измерительные зонды непосредственно в ядро ОС;

o задавать набор функций, на которые будут устанавливаться зонды;

o задавать логику алгоритм работы зонда;

o измерять время выполнения функций в тактах процессора, что дает возможность учесть аппаратную реализацию однопроцессорной ЭВМ.

Указанные преимущества играют большую роль для оценки методической погрешности, вносимой измерительными зондами, однако, широкие возможности по установке и выбору алгоритма работы зондов предполагают решение ряда вопросов, таких как: что и где замерять?

Рассмотрим схему стенда исследований, представленную на рис. 1.

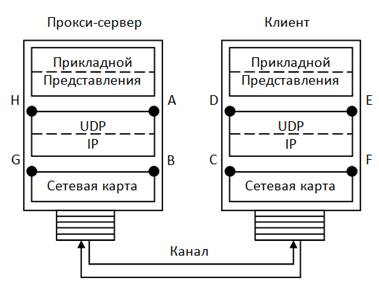
Рис. 1. Схема стенда исследований

На рис. 1 отмечены ключевые точки A,B,C,D,E,F,G,H задействованные в ОС при обработке сетевого трафика. Времена обработки функций, расположенных внутри каждого промежутка между двумя соседними точками, представляют собой временные интервалы, которые затрачены для обработки сетевого трафика, определяющие вероятностно-временные характеристики прокси-сервера по обработке сетевого трафика. Отметим наиболее интересные промежутка AB, EF, DC и HG, которые представляют временные интервалы обработки принимаемых (, ) и отправляемых (, ) требований сети.

Следует подчеркнуть что, нахождение отмеченных точек внутри ОС и разработка алгоритма зонда представляются не тривиальными задачами, которые не рассматриваются в настоящей статье.

В дальнейшем изложении принимаем, что местоположение точек определено и поставлено в соответствие с функциями алгоритма ОС.

Также в данной статье будем считать, что алгоритм зонда линейный и одинаковый для всех зондов.

Работу ЭВМ по обработки сетевого трафика можно разбить на две фазы:

o фазу приема требования;

o фазу отправки требования.

Очевидно, что эти две фазы кардинально отличаются друг от друга алгоритмами работы, а, следовательно, и набором программных функций, выполняемых ОС.

Установка измерительных зондов в указанных точках позволяет найти требуемые вероятностно-временные характеристики.

Однако, результаты измерений интервалов времени между точками: AB, CD, EF и GH, - позволяют получить данные, схожие по точности с данными «черного ящика». Причина низкой точности в том, что алгоритм приема и отправки требований сети весьма сложен и подразумевает операции ветвления и циклов, при этом входящие требования могут отличаться по типу сетевого протокола. В результате при переходе от одного эксперимента к другому эксперименту, получаем неоднородные данные с большой дисперсией.

Для решением данной проблемы требуется установка зондов на каждую из программных функций ОС, выполняющих прием и отправку требований.

На основании изложенного исходными данными для предлагаемой модели являются:

– доля трафика, доставленная по определенному протоколу (i), относительно общего трафика, обрабатываемого прокси-сервером;

– вероятность появления j-той функции при обработке требований протокола типа i, определяется как количество экспериментов, в которых зафиксировано выполнение j-той программной функции к общему количеству экспериментов;

– частота выполнения j-той функции при обработке требований протокола типа i.

M() – математическое ожидание времени выполнения j-той функции при обработке требований протокола типа i.

За основу модели прокси-сервера выбирается модель предложенная Абросимовым Л.И, которая представлена в [3]. Предложенная модель прокси-сервера представлена в графическом виде на рис. 2:

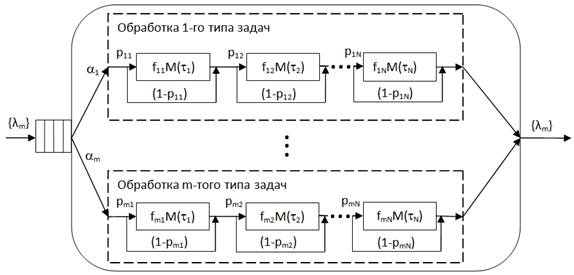
Рис. 2. Графическое представление предложенной модели прокси-сервера

Предложенная модель отличается от известной тем, что вместо абстрактных «элементов алгоритма» рассматриваются конкретный набор сетевых функций протоколов, входящих в состав ядра ОС Linux, вместо абстрактных цепочек элементов алгоритма рассматриваются цепочки, описывающие фазы сетевых протоколов, выполняют функции приема и обработки требований; предложенная модель использует измеряемые параметры частоты {} использования m-тым сетевым протоколом i-той сетевой функции

Для математического описания модели необходимо знать закон распределения потока входящих сообщений, а так же закон распределения времен обслуживания. Принимаем, что законы распределения экспоненциальными, тогда для модели СМО M|M|1∞ можно определить количество n сообщений в моделируемом узле по формуле (1)

где ρ – коэффициент загрузки моделируемого узла.

Однако, формула (1) не учитывает разделения входящих требований по типам протоколов и не учитывает разбиения обработки на фазы. Для разбиения требований по типам воспользуемся методом контуров и будем считать, что для одного контура (q) потока требований приходят требования протоколов только одного типа.

Учитывая, что фазы обслуживания следуют непосредственно одна за другой, в предложенной модели математическое ожидание времени обслуживания каждой фазы определяется как сумма математических ожиданий времени выполнения каждой функции умноженных на частоту и вероятность выполнения сетевой функции протокола

Если же принять во внимание, что прием и обработка происходят в разное время, то необходимо будет учесть время нахождения сгенерированного ответа в очереди. Отметим, что, так как мы приняли законы распределения экспоненциальными, а времена выполнения функций считаем независимыми событиями, то по теореме сложения математических ожиданий:

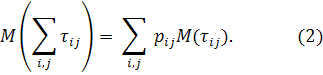
Для каждого контура q формула, определяющая количество требований в системе (в узле и очереди) определяется по соотношению (2):

где q – контур, R – общая интенсивность обслуживания равная ,

- интенсивность поступления требований q-го контура.

Тогда формула модели прокси-сервера для определения количества n требований в системе будет выглядеть следующим образом:

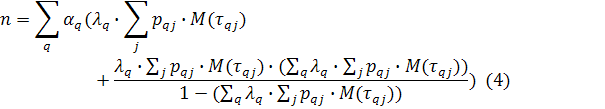
В результате получена формула (4) для расчета количества n требований в системе, учитывающая разбиение входящих требований на типы по используемому для их передачи протоколу, который определяется контуром q и фазой обслуживания.

Отметим, по найденному количеству n требований можно определить среднее время пребывания требования в прокси-сервере (в очереди и на обслуживании), применяя формулу Литтла:

Литература

1. Таненбаум Э., Уэзеролл Д. Компьютерные сети. 5-е изд. – СПб.: Питер, 2012. – 960 с.: ил.

2. Chrisian Benvenuti Understanding Linux Network Internals. – O`Reilly, 2005. – 1062 c.

3. Абросимов Л. И. Методология анализа вероятностно-временных характеристик вычислительных сетей на основе аналитического моделирования. Диссертация на соискание ученой степени