BC/NW 2012; №2 (21):6.1

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЫЧИСЛИТЕЛЬНОГО КОМПЛЕКСА ОБРАБОТКИ ГЕОФИЗИЧЕСКИХ ДАННЫХ

Рыбинцев В.О., Домаров Ю.Н.

Обработка и интерпретация данных геофизических исследований (геофизической разведки) – задача сложная и трудоемкая, однако имеющая важнейшее практическое значение. Процесс обработки, например, результатов сейсморазведки, сопряжен с проведением серьезных вычислений, относящихся к категории high-performance computing (HPC) [1]. Успешное решение таких задач возможно только при использовании специализированных высокопроизводительных вычислительных систем. Непосредственно результаты разведки представляют собой огромные массивы информации – терабайты данных, для работы с которыми необходимо использование мощных систем хранения (задачи обработки геофизических данных относятся к категории data-intensive computing) [2]. Вычислительный комплекс для решения геофизических задач включает в себя: высокопроизводительную вычислительную систему, а именно вычислительный кластер (ВК), систему хранения данных (СХД) – дисковый массив большого объема, а также высокоскоростной коммутатор, соединяющий между собой ВК и СХД. При построении и модернизации подобных вычислительных комплексов встает проблема выбора конфигурации их компонент и оценки общей производительности комплекса для определения согласованных между собой характеристик ВК и СХД. В данном случае необходимо рассматривать всю систему как единое целое, в тоже время большинство существующих моделей и методов определения производительности касаются либо только вычислительных кластеров, либо только систем хранения.

В настоящей статье приводится математическая модель вычислительного комплекса обработки данных, а также основные расчетные соотношения для определения ее параметров.

Итак, в состав рассматриваемого вычислительного комплекса входят кластер, дисковая система и коммутатор. Все компоненты системы соединяются между собой посредством высокоскоростной коммуникационной среды (10 Gigabit Ethernet, Fibre Channel, InfiniBand). Вычислительный кластер строится из набора стандартных многопроцессорных многоядерных вычислительных узлов (node), объединенных между собой внутренней коммутационной сетью. Система хранения данных – дисковый массив, разбитый на виртуальные тома (volume). В отличие от математической модели, разработанной в [3], предлагаемая модель учитывает коммуникационную среду, связывающую узлы ВК и тома СХД. Для построения математической модели рассматриваемого комплекса используется метод контуров [4], позволяющий естественным образом отобразить в модели процесс продвижения информации: исходные данные считываются из СХД, передаются на вычислительный узел ВК, а после обработки записываются обратно на диск.

Вычислительный комплекс рассматривается как замкнутая стохастическая сеть массового обслуживания (СеМО). Источником заявок в сети являются C вычислительных ядер в каждом из N узлов ВК. Все заявки через коммутатор поступают в СХД, представленную как V независимых томов. Предполагается, что все узлы ВК и тома СХД одинаковы по своим характеристикам и в процессе решения задачи загружаются равномерно, соответственно равновероятно попадание заявки в любой из узлов кластера и на любой том системы хранения. Любая заявка проходит каждый из элементов сети дважды, что также отражено в модели. Модель комплекса представлена на рис. 1.

Распределение времени обслуживания заявок в кластере, системе хранения и коммутаторе является существенно не экспоненциальным. Поток заявок на входе и соответственно распределение интервалов времени поступления заявок также не является экспоненциальным. Исходя из этого, для расчета математической модели необходимо использовать формулы для систем массового обслуживания общего вида GI/G/1. Однако точных соотношений, описывающих параметры систем такого рода нет, поэтому при аналитических расчетах обычно используются приближенные соотношения [5].

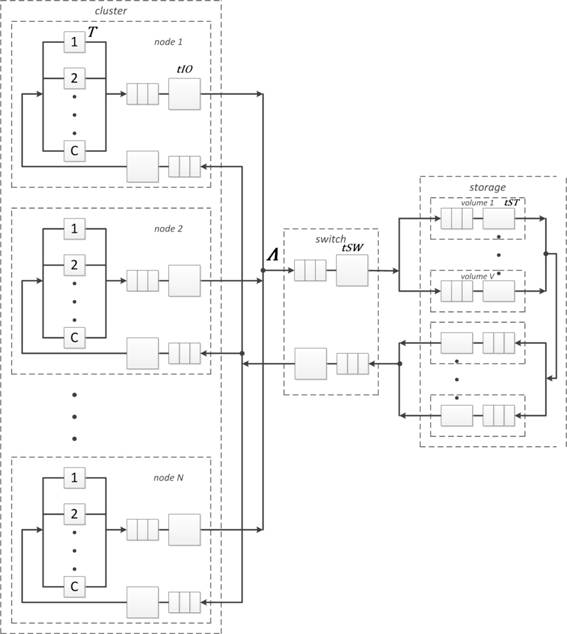
Рис. 1. Математическая модель вычислительного комплекса

Для расчета параметров математической модели необходимо сначала составить нелинейное уравнение баланса заявок в системе. Общее число заявок в системе равно сумме среднего числа заявок в кластере, коммутаторе и дисковой системе. В тоже время число заявок ограничено и равно произведению числа ядер в узле на количество узлов кластера:

Среднее число заявок в коммутаторе равно:

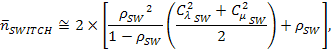
среднее число заявок в системе хранения есть сумма средних для каждого тома:

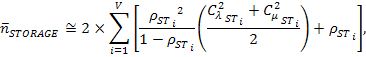
а среднее число заявок в кластере также можно получить как сумму средних для каждого узла:

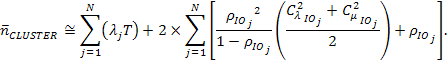
Приняв во внимание то, что все узлы кластера и все тома системы хранения однотипные, получим итоговое выражение для уравнения баланса заявок в системе:

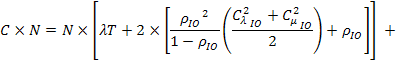
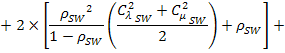
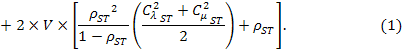
Численное решение уравнения (1) при заданных временных и вероятностных характеристиках СеМО позволит вычислить значение интенсивности поступления заявок в систему, а следовательно и значения всех параметров модели. Времена и значения вероятностных коэффициентов в свою очередь можно найти по результатам эксперимента либо моделирования работы комплекса.

Зная значения среднего числа заявок в каждом из узлов системы можно воспользовавшись формулой Литтла определить среднее время пребывания заявки в каждом из этих узлов. Это даст возможность получить выражение для общего времени решения задачи (или времени цикла решения задачи), а затем составить по нему целевую функцию, минимизации, которая необходима для решения задачи оптимизации для определения характеристик ВК и СХД.

По формуле Литтла имеем (M – количество циклов решения задачи):

Так как в данном случае минимизация общего времени решения эквивалентна минимизации времени одного цикла, то целевую функцию можно записать в следующем виде:

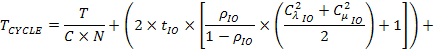
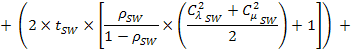
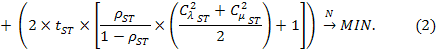
Полученное уравнение баланса (1) позволяют определять параметры математической модели комплекса по известным характеристикам его компонентов, которые могут быть получены, например, по результатам тестирования или моделирования работы оборудования. Целевая функция (2) может быть использована в дальнейшем для решения прямой (известны параметры СХД) или обратной (известны параметры ВК) задачи оптимизации и определения оптимальной по критерию производительности конфигурации вычислительного комплекса.

Литература

1. Суперкомпьютерные технологии в науке, образовании и промышленности (первый выпуск) / под редакцией: Садовничего В.А., Савина Г.И., Воеводина Вл.В. – М.: Издательство Московского университета, 2009. – 232с.

2. Курин Е.А. Сейсморазведка и суперкомпьютеры / Вычислительные методы и программирование. Том 12. с.34-39.

3. Рыбинцев В.О., Домаров Ю.Н. Математическая модель вычислительного комплекса для решения задач высокопроизводительной обработки больших объемов информации / Труды XIX МНТК «Информационные средства и технологии». В 3-х томах. Том 1. – М.: Издательский дом МЭИ, с.297-301.

4. Абросимов Л.И. Анализ и проектирование вычислительных сетей. – М.. Издательство МЭИ, 2000. – 52с.

5. Рыбинцев В.О. Разработка декомпозиционного метода расчета характеристик эффективности функционирования диалоговых локальных вычислительных сетей. Диссертация на соискание ученой степени кандидата технических наук. Москва, 1985.