BC/NW 2012; №2 (21):8.1

ИСПОЛЬЗОВАНИЕ МЕТОДА БРОКЕРА ПРИ ОЦЕНКЕ И РЕЗЕРВИРОВАНИИ ПРОПУСКНОЙ СПОСОБНОСТИ КАНАЛОВ

Широков В.Л.

Введение

Важными особенностями современных телекоммуникаций являются:

· распределённость функций управления,

· передача мультисервисной информации,

· недетерминированный характер связей между элементами системы.

При этом трафик становится все более мультимедийным, а сеть превращается в мультисервисную систему обмена информацией (МСОИ) [1], приобретая свойства сложного динамического объекта. Поэтому, для обеспечения надежности соединений, необходимо оценивать загрузку каналов, резервировать пропускную способность (сетевые ресурсы). Иначе, из-за возникновения локальных перегрузок, будут происходить разрывы соединений.

Модель МСОИ – это динамическая высокоскоростная, причём замкнуто-разомкнутая сеть очередей. Методология анализа [2] ресурсно-временных параметров МСОИ при проектировании таких систем включает в себя необходимые математические модели и методики:

· модель нагрузки;

· модель производительности;

· модель функционирования сети;

· методики расчета, оценки, балансировки нагрузки на МСОИ.

Целевой функцией при балансировке нагрузки является соотношение между числом абонентов передачи данных, видео и услуг телефонии.

Методология [2] позволяет рассчитывать параметры МСОИ по заданной проектной нагрузке, модернизировать сеть, выбирать сценарии развертывания оборудования с учетом выделенного бюджета, роста числа абонентов на этапе проектирования или модернизации сети.

Однако для рабочего режима функционирования МСОИ необходимо также оперативно оценивать нагрузку, распределять сетевые ресурсы, резервировать пропускную способность в реальном времени.

В качестве одного из методов оценки и прогнозирования нагрузки предлагается использовать метод брокера с фильтрацией Калмана.

1. Оценка и прогнозирование трафика

Рассмотрим, как показано на рис.1, автономные сегменты AS1, AS2, принадлежащие возможно разным доменам (регионам сети), между a и b хостами которых существует виртуальный канал, линк (линия) l(1,2).

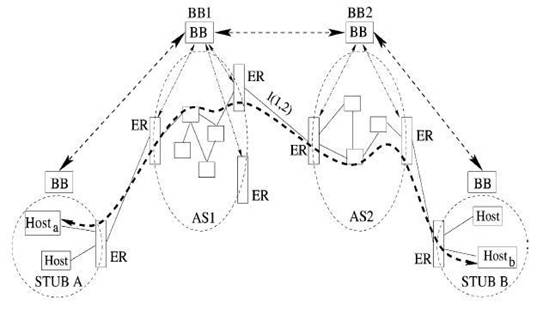
Рис. 1. Топология сети

Обозначения:

BB – брокер полосы пропусканя (Bandwidth Broker, БП),

ER – пограничный роутер (Edge Router, маршрутизатор).

Каждый сегмент (регион сети) имеет своего брокера полосы пропускания (BB1, BB2 соответственно), ассоциированный с ним.

Оценим уровень трафика между этими доменами для заданного класса трафика, основываясь на измерениях агрегированного трафика в линии l(1,2). Предполагается, что измерения трафика выполняются в дискретных временных точках mT, m=1,2,…,M с периодом дискретизации T. Значение T – это заданная величина, означающая периодичность измерений. Большие значения T дают более редкие оценки, которые могут стать результатом больших ошибок.

В момент времени m (соответственно до mT) агрегированный трафик заданного класса в линии l(1,2) от AS1 к AS2 обозначим как y(m). Так же принимается, что в течение всего интервала (0,MT] количество установленных сессий, которые используют l(1,2), равно N. Сервисные потоки в каждой сессии – это активные периоды. Каждая сессия состоит из множества потоков, разделенных периодами бездействия.

Без ограничения общности сконцентрируемся на одном классе трафика и прогнозировании ресурса пропускной способности для него.

Для рассмотрения сценария с различными классами трафика, то есть с разными требованиями к пропускной способности, аналогичный анализ может быть расширен и применён к каждому классу. Речь идет о распределении ресурсов для разных классов сервиса DiffServ, для которых допускается предположение о фиксированной потребности в ресурсах.

Для описания потоков за основу принимается модель Пуассона с экспоненциально распределёнными интервалами времени между прибытиями (параметр λ) и длительностями обслуживания пакетов (параметр µ). Общеизвестно, что IP-трафик на пакетном уровне является сложным. Это вытекает из характеристик потокового уровня, когда популяция пользователей большая. Каждый пользователь вкладывает небольшую порцию в полный трафик, а независимость естественно приводит к процессу Пуассона [3]. Приводимый ниже анализ проводился с учетом этого ограничения, а эксперименты показали, что прогнозируемая емкость очень близка реальному трафику.

Схема резервирования ресурсов по методу брокера делится на два этапа:

на первом этапе выполняется грубое измерение агрегированного трафика y(m), и оно используется для оценки количества потоков через фильтр Калмана.

на втором этапе резервируются ресурсы R(m) в линии l(1,2) для времени t∈(mT,(m+1)T] на базе прогнозной оценки x(m).

Далее приведем краткую теорию дискретной фильтрации Калмана.

2.1. Дискретный фильтр Калмана

Фильтр Калмана [4] – это система уравнений, которые обеспечивают вычислительное (рекурсивное) решение методом наименьших квадратов. В нем реализуется оценка по методу предиктор-корректор, что является оптимальным в том смысле, что сводится к минимуму разброс (ковариация) ошибочных оценок. Процесс оценивается с помощью обратной связи. Обеспечивается оценка прошлого, настоящего и будущего состояний, даже если знание точного характера моделируемой системы недостаточно. Фильтр Калмана пытается оценивать состояние x управляемого процесса в дискретном времени.

Пусть система описывается вектором состояния x, наблюдается во времени m=0,1,… и описывается линейными стохастическими разностными уравнениями

x(m+1) = Ax(m) + Bu(m) + w(m). (1)

Каждое наблюдение, однако, искажается шумами и, таким образом, фактическое измерение ỹ в моменты времени m = 0,1,… задается как

ỹ(m) = Cx(m) + v(m). (2)

Случайные переменные w(m) и v(m) представляют собой соответственно процесс и измеренный шум. Они считаются независимыми процессами, а шум белым Гауссовским с нулевым средним [5].

E[w(m)w(k)] = , при k = m; = 0, в противном случае,

E[v(m)v(k)] = , при k = m; = 0, в противном случае,

E[v(m)w(k)] = 0. (3)

Параметр A в уравнении (1) относится к состояниям на предыдущем и текущем временных шагах при отсутствии или самой функции, или шума. Предполагается, что A остается константой при анализе. Параметр B относится к дополнительному влиянию по входу u на состояние x, в то время как параметр C в уравнении (2) определяет отношение к измеренному значению. Объективно фильтр Калмана должен обеспечивать «наилучшую» оценку, при некоторой подходящей чувствительности на базе наблюдаемых значений ỹ(m) и знании статистических свойств измеренного шума. В соответствии с механизмом фильтрации Калмана, наилучшая оценка для x(m) может быть получена рекурсивно из предыдущей наилучшей оценки и её ковариационной матрицы. Таким образом, фильтр Калмана можно разделить на два шага: предсказание и коррекция.

Представим далее дискретный фильтр Калмана.

Уравнение состояния: x(m) = A(m-1)x(m-1)+Bu(m-1)+w(m-1).

Уравнение наблюдения: y(m) = C(m)x(m)+v(m).

Шаг 1: инициализация (0|0) = E[x(0)],

P(0|0) = E[x(0)x(0)^T] = .

Шаг 2: вычисления для m=1, 2, … ;

шаг предсказания:

(m|m-1) = A(m-1) (m-1|m-1) + Bu(m),

P(m|m-1) = A(m-1)P(m-1|m-1) (m-1) +

шаг коррекции:

k(m)= P(m|m-1) (m)[C(m)P(m|m-1) (m) + ]-1

(m|m) = (m|m-1) + k(m)[y(m) - C(m) (m|m-1)

P(m|m) = {I - k(m)C(m)}P(m|m-1).

Первый шаг отвечает за предварительное предсказание текущего состояния во времени для получения априорных оценок состояния и вычисления ковариации для следующего временного шага. Второй шаг отвечает за обратную связь для получения улучшенной апостериорной оценки.

2.2. Оценка трафика

Измеримая переменная в системе ỹ(m) является измерением агрегированного трафика в канале на фоне шума. Номинально x(m) = y(m)/b, но у нас нет доступа к правильному измерению y(m), даже если это известная величина для определенного класса трафика. Таким образом, предлагается использовать настройки фильтра Калмана для оценки (m), чтобы оценить действительное значение x(m), используя измерения ỹ(m) с шумами. Реальное измерение уровня шума дает ỹ(m) с шумом. Другими словами, измерения, полученные из сети для мгновенного трафика в канале, могут быть с шумами из-за просчетов, смещения во времени и т.д. Чтобы использовать настройки фильтра Калмана, нужно найти связь между x(m) и y(m), и x(m) и x(m+1). С этой целью мы определяем (t), t∈(mT,(m+1)T] вероятность того, что количество активных потоков в момент времени t есть k, т.е. для t∈(mT,(m+1)T]

(t) = prob{x(t)=k} . (4)

Диаграмма перехода между соседними состояниями системы показана на рис.2.

Рис. 2. Диаграмма перехода состояний

Из этой диаграммы, используя теорию очередей [3], можно записать дифференциальные уравнения (5)–(7) для вероятности (t):

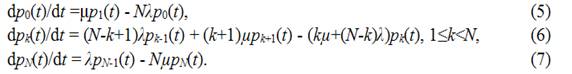
Производящая функция G(z,t) определяется как преобразование функции распределения вероятностей. Это помогает при вычислении среднего и дисперсии распределения вероятностей. Далее вычисляется G(z,t) с помощью формул (5)–(7)

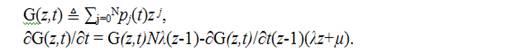
Используя начальное условие G(z,mT) = , т.е. количество активных потоков в момент mT есть x(m), получаем следующее решение для G(z,t) для t∈(mT,(m+1)T],

где

По определению производящей функции и свойств z-преобразования получим

Сравнивая это уравнение с фильтром Калмана (уравнения (2) и (3)), получаем

Таким образом, из начальных установок фильтра Калмана, получим

где k(m) – усиление фильтра Калмана по определению (см. выше).

Уравнение (10) дает текущую оценку трафика в канале. Эта оценка используется, чтобы прогнозировать трафик с целью резервирования ресурсов. Однако это требует отдельного рассмотрения.

Литература

1. Широков В.Л. Разработка моделей и методов для оценки и выбора параметров МСОИ. Диссертация. к.т.н. – МЭИ (ТУ). – 2006.

2. Широков В.Л. Методология создания беспроводных мультисервисных сетей класса WiMAX. Ч. 1-3 // Технологии и средства связи. - № 1, 3, 5. - 2010. - С.32-33, 24-25, 36-37.

3. J.W. Roberts, Traffic theory and the Internet, IEEE Communications Magazine 39 (1) (2001) 94–99.

4. P.S. Maybeck, Stochastic Models, Estimation, and Control, Academic Press, New York, 1979.

5. B. Cipra, Engineers look to Kalman filtering for guidance, SIAM News 26 (5), 1993.