BC/NW 2013, №2 (23): 7.1
ИССЛЕДОВАНИЕ ТОЧНОСТИ СИСТЕМЫ WI-FI ПОЗИЦИОНИРОВАНИЯ, ПОСТРОЕННОЙ С ИСПОЛЬЗОВАНИЕМ МЕТОДА k-БЛИЖАЙШИХ СОСЕДЕЙ
Ассур О.С., Филаретов Г.Ф.
(ФГБОУ ВПО «Национальный исследовательский университет «МЭИ», Москва, Россия)
Системы Wi-Fi позиционирования строятся как системы классификации, которые на основе вектора входных признаков (информация об уровнях мощности сигнала) с использованием обучающей выборки выносят суждение об отнесении этого вектора к некоторому классу (позиция устройства). Задача построения такой системы делится на два этапа – построение обучающей выборки наблюдений, на основании которой будет решаться задача классификации и выбор и настройка метода классификации.
Одним из основных методов позиционирования, используемых при позиционировании объектов пространстве, является модифицированный метод k-ближайших соседей, описанный в [1]. При использовании данного метода определение местоположения объектов производится как вычисление взвешенного центра масс фигуры, формируемой в признаковом пространстве k-ближайшими соседями по формуле (1).
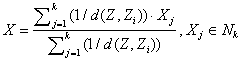 , (1)
, (1)
где ![]() -
неизвестные координаты точки,
-
неизвестные координаты точки, ![]() - координаты j-ой точки
обучающей выборки,
- координаты j-ой точки
обучающей выборки, ![]() ,
,
![]() – векторы
измерений мощности сигнала Wi-Fi выбранных точек доступа, k – количество
ближайших соседей,
– векторы
измерений мощности сигнала Wi-Fi выбранных точек доступа, k – количество
ближайших соседей, ![]() –
Евклидово расстояние между векторами
–
Евклидово расстояние между векторами ![]() и
и ![]() (2).
(2).
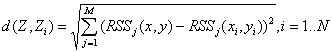 , (2)
, (2)
где М – размерность
признакового пространства (количество используемых системой точек доступа), ![]() - уровень мощности
сигнала Wi-Fi от
j-ой точки доступа в точке с координатами (x,y).
- уровень мощности
сигнала Wi-Fi от
j-ой точки доступа в точке с координатами (x,y).
Параметром настройки метода k-ближайших соседей, описанного в [1], является количество ближайших соседей k. При этом в литературе по данной тематике [2-3] не исследуется влияние используемой в методе метрики расстояния на точность системы позиционирования. Везде по умолчанию используется Евклидово расстояние, которое в общем случае сложной интерференционной картиной распространения Wi-Fi сигналов в помещениях может являться не оптимальным.
В рамках проведенного исследования была произведена экспериментальная настройка системы Wi-Fi позиционирования, построенной с использованием метода k-ближайших соседей. В качестве параметров настройки были выбраны количество ближайших соседей и метрика расстояния. Количество ближайших соседей выбиралось из множества {3, 5, 7, 9}. В качестве альтернативных к Евклидовой метрике расстояния были выбраны Манхэттенское расстояние (3) и метрика Чебышева (4).
![]() (3)
(3)
![]() (4)
(4)
В качестве критериев точности позиционирования при экспериментальной настройке были выбраны средняя ошибка позиционировании, максимальная ошибка позиционирования и количество измерений с ошибкой выше среднего.
Измерения уровней мощности сигналов Wi-Fi производились в демонстрационном зале компании ООО «НИИ СОКБ», план которого представлен на рис. 1. Выбор помещения был сделан, во-первых, в связи с наличием в указанном помещении достаточного для решения задачи позиционирования количества точек доступа, а во-вторых, в связи со сложной интерференционной картиной распределения сигналов Wi-Fi в пространстве в связи с наличием предметов, которые существенно искажают эту картину (стеклянные шкафы и металлические конструкции).

Рис. 1. План демонстрационного зала ООО «НИИ СОКБ»
Полученные расчетные значения критериев точности позиционирования представлены в таблицах 1 (для Евклидовой метрики), 2 (для Манхэттенского расстояния) и 3 (для метрики Чебышева).
Таблица 1.
Точность позиционирования при использовании Евклидовой метрики
|
|
k = 3 |
k = 5 |
k = 7 |
k = 9 |
|
Средняя ошибка |
1,47 |
1,52 |
1,57 |
1,62 |
|
Максимальная ошибка |
5,89 |
5,32 |
5,27 |
5,17 |
|
Количество с ошибкой выше среднего, % |
39,22 |
40,63 |
41,41 |
42,50 |
Таблица 2
Точность позиционирования при использовании Манхэттенского расстояния
|
|
k = 3 |
k = 5 |
k = 7 |
k = 9 |
|
Средняя ошибка |
1,35 |
1,46 |
1,49 |
1,53 |
|
Максимальная ошибка |
5,84 |
5,29 |
4,89 |
4,57 |
|
Количество с ошибкой выше среднего, % |
37,50 |
40,63 |
40,78 |
41,88 |
Таблица 3
Точность позиционирования при использовании метрики Чебышева
|
|
k = 3 |
k = 5 |
k = 7 |
k = 9 |
|
Средняя ошибка |
1,61 |
1,68 |
1,71 |
1,75 |
|
Максимальная ошибка |
5,82 |
5,58 |
5,58 |
5,55 |
|
Количество с ошибкой выше среднего, % |
40,16 |
40,31 |
41,25 |
42,66 |
На основании полученных результатов в качестве параметров метода позиционирования были выбраны Манхэттенское расстояние и количество ближайших соседей k = 7. При этих параметрах было получении минимальное значение максимальной ошибки позиционирования, при этом значение средней ошибки также было на достаточно низком уровне.
После экспериментальной настройки системы позиционирования было проведено исследование ее точности в on-line режиме. В ходе исследования точности системы позиционирования в on-line режиме был проведен следующий эксперимент – устройство перемещалось с постоянной скоростью 1 м/с из позиции 1 в позицию 2 (рис. 2) с остановкой в контрольных позициях на 30 секунд.
Результаты проведенного исследования точности системы позиционирования в on-line режиме представлены на рис. 2 и рис. 3.
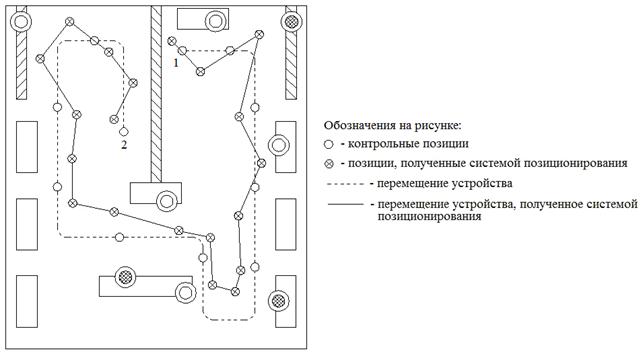
Рис. 2. График перемещения устройства и определение движения устройства системой позиционирования
На рис. 2 представлены истинный график перемещения объекта и график перемещения, полученный системой позиционирования. На рис. 3. представлен график перемещения устройства, на котором с помощью окружностей показаны максимальные ошибки в определении контрольных позиций графика перемещений устройства.
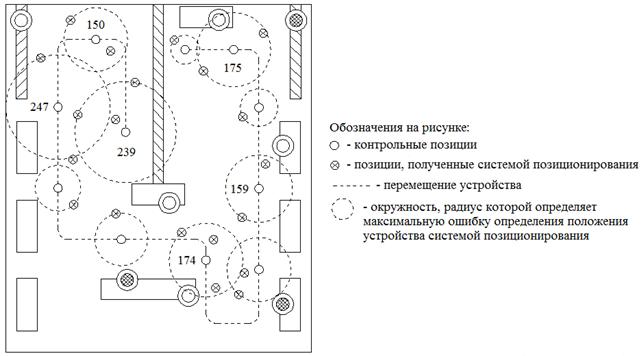
Рис. 3. График перемещения устройства и ошибки, получаемые системой позиционирования
Как видно из рис. 2 и рис. 3, система позиционирования объектов в пространстве, построенная с использованием метода k-ближайших соседей, позволяет определять местоположение устройства с достаточной точностью. Средняя ошибка позиционирования составляет 1,49 м., максимальная - 4,89 м.
Литература
1. Frédéric Evennou and François Marx. Advanced Integration of WiFi and Inertial Navigation Systems for Indoor Mobile Positioning. EURASIP Journal on Advances in Signal Processing
2. Bahl P, Padmanabhan VN. RADAR: An in-building RF based user location and tracking system, In Proceedings of IEEE Infocom, 2000, pp. 775–784
3. Bahl P, Padmanabhan VN, Balachandran A. Enhancements to the RADAR User Location and Tracking System, Microsoft Research Technical Report: MSR-TR-00-12, 2000