BC/NW 2013, №2 (23): 8.1
СЖАТИЕ ИЗОБРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ ВЭЙВЛЕТ-
ПРЕОБРАЗОВАНИЙ
Артюхов О.И., Герасимов В.В., Кузнецов С.В..
(ФГБОУ ВПО «Национальный исследовательский университет «МЭИ»,
Москва, Россия)
(Московский институт радиотехники, электроники и автоматики
(Технический университет), Россия)
Вэйвлеты являются сравнительно новым изобретением в прикладной математике. Это название само по себе возникло около десятилетия тому назад. За последние десять лет интерес к ним вырос. Их нынешний успех объясняется несколькими причинами. С одной стороны, концепция вэйвлетов может рассматриваться как синтез идей, возникших за последние двадцать или тридцать лет в технике, физике и чистой математике. Вследствие своего междисциплинарного происхождения, вэйвлеты представляются привлекательными для математиков и инженеров с самыми разными научными интересами. С другой стороны, вэйвлеты являются довольно простым математическим инструментом с большим разнообразием возможностей для применения. Они были успешно применены для анализа сигналов и изображений.
При любом подходе к решению задачи обработки фото/видеоданных объектом исследования является изображение. Прежде чем использовать для решения задач обработки изображений какие-либо методы, необходимо точно знать, какой метод и с какими параметрами применим для достижения поставленной задачи .
Необходимо заметить, что вэйвлет-компрессия изображений даёт лучшие показатели по сравнению с другими методами компрессии изображений, а именно, даёт более высокую степень сжатия файла с изображением при приемлемых для конкретной задачи потерях качества изображения. Именно поэтому интерес к вэйвлет-компресии постоянно растет.
Вэйвлетное сжатие — общее название класса методов кодирования изображений, использующих двумерное вэйвлет-разложение кодируемого изображения или его частей. Обычно подразумевается сжатие с потерей качества. Существенную роль в алгоритмах вэйвлетной компрессии играет концепция представления результатов вэйвлет-разложения в виде нуль-дерева (zero-tree). Упорядоченные в нуль-дереве (рис. 1) битовые плоскости коэффициентов вэйвлет-разложения огрубляются и кодируются далее с использованием статистических методов сжатия [4].
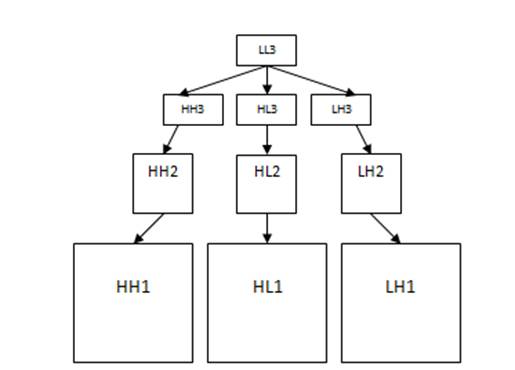
Рис.1. Нуль-дерево вэйвлет-разложения
Вэйвлетная компрессия в современных алгоритмах компрессии изображений позволяет значительно (до двух раз) повысить степень сжатия чёрно-белых и цветных изображений при сравнимом визуальном качестве по отношению к алгоритмам предыдущего поколения, основанным на дискретном косинусном преобразовании, таких, например, как JPEG.
Для работы с дискретными изображениями используется вариант вэйвлет-преобразования, известный как алгоритм Малла, названный в честь его изобретателя Стефана Малла. Исходное изображение раскладывается на две составляющие — высокочастотные детали (состоящие в основном из резких перепадов яркости), и сглаженную уменьшенную версию оригинала. Это достигается применением пары фильтров, причём каждая из полученных составляющих вдвое меньше исходного изображения. Как правило, используются фильтры с конечным импульсным откликом, в которых пикселы, попавшие в небольшое «окно», умножаются на заданный набор коэффициентов, полученные значения суммируются, и окно сдвигается для расчёта следующего значения на выходе.
Алгоритм JPEG, в отличие от вэйвлетного, сжимает по отдельности каждый блок исходного изображения размером 8 на 8 пикселов. В результате при высоких степенях сжатия на восстановленном изображении может быть заметна блочная структура. При вэйвлетном сжатии (рис. 3) такой проблемы не возникает, но могут появляться искажения другого типа, имеющие вид «призрачной» ряби вблизи резких границ. Считается, что такие артефакты в среднем меньше бросаются в глаза наблюдателю, чем «квадратики», создаваемые JPEG (рис. 2).
|
|
|
|
Рис.2. Сжатие JPEG (7959 байт) |
Рис. 3. Вэйвлет-сжатие |
Реализованный метод является аналогом известного алгоритма вэйвлетного сжатия JPEG 2000. Здесь используется быстрый лифтинг дискретного биортогонального CDF 9/7 вэйвлета, используемый в алгоритме сжатия изображений JPEG 2000. Таким образом, используя вэйвлетное сжатие, можно получить изображение с соизмеримыми потерями у JPEG, но зато человеческим глазом такая картинка воспринимается лучше, т.к. нет ярко выраженных пикселей и полос. Алгоритмы сжатия, используемые при создании файлов, делятся на два класса:
Сжатие без потерь - по сжатым данным можно полностью восстановить исходную информацию.
Сжатие с частичной потерей информации - если допускается неточное восстановление сжатых данных.
Если исходная информация представлена в виде последовательности букв: ААААААБББВВВВВААААА, то ее можно представить следующим образом А5БЗВ5А5, используя символ буквы и число ее повторений в последовательности. При этом уменьшается объем данных в 2,7 раз. Алгоритм декодирования этой последовательности очевиден. Если изображение содержит большие области одинаковых пикселей, то будет получен очень неплохой результат [6].
Как пример – преобразование Хаара. Цель — преобразовать изображение так, чтобы оно хорошо сжималось классическими алгоритмами. Его нужно изменить так, чтобы получить длинные цепочки нулей.
У «реальных» изображений, таких как фотографии, есть одна особенность — яркость соседних пикселей обычно отличается на небольшую величину. В мире редко можно увидеть резкие, контрастные перепады яркости. А если они и есть, то занимают лишь малую часть изображения.
Рассмотрим фрагмент первой строки яркостей из известного изображения «Lenna»: 154, 155, 156, 157, 157, 157, 158, 156
Рис. 4. Стандартное тестовое изображение Lenna
Соседние числа очень близки. Чтобы получить желаемые нули или хотя бы близкое к ним, можно закодировать отдельно первое число, а потом рассматривать лишь отличия каждого числа от предыдущего, при этом получим:
154, 1, 1, 1, 0, 0, 1, -2.
Такой метод называется дельта-кодированием. Но у него есть серьёзные недостаток — он нелокальный. Возможно сделать иначе. Разобьём все числа на пары и найдём полусуммы и полуразности значений в каждой из них.
(154, 155), (156, 157), (157, 157), (158, 156)
(154.5, 0.5), (156.5, 0.5), (157, 0.0), (157, -1.0)
Полусумма — это среднее значение яркости пары пикселей. А полуразность несёт в себе информацию об отличиях между значениями в паре. Очевидно, зная полусумму «a» и полуразность «d», можно найти и сами значения: первое значение в паре = a - d, второе значение в паре = a + d. Теперь полученные числа можно перегруппировать, разделив полусуммы и полуразности: 154.5, 156.5, 157, 157; 0.5, 0.5, 0.0, -1.0.
Числа во второй половине последовательности как правило будут небольшими . Как мы уже выяснили раньше, в реальных изображениях соседние пиксели редко отличаются друг от друга значительно. Если значение одного велико, то и другого велико. В таких случаях говорят, что соседние пиксели коррелированы.
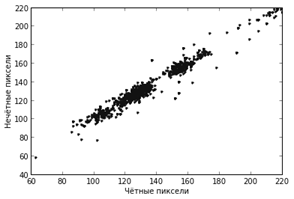
Рассмотрим первые 2000 пар соседних пикселей и каждую пару представим на графике точкой. Все точки выстраиваются вдоль одной прямой линии. И так практически во всех реальных изображениях. Верхний левый и нижний правый углы изображения практически всегда пусты.
|
Рис. 5. Пары соседних пикселей |
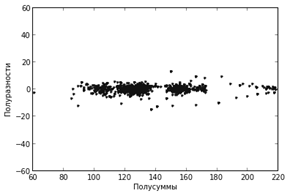
Рис. 6. Полусуммы и полуразности |
Видно, что полуразности находятся в гораздо более узком диапазоне значений. А это значит, что на них можно потратить меньше одного байта.
Полусуммы усредняют значения яркостей, то есть «отфильтровывают» случайные всплески значений. Можно считать, что это некоторый частотный фильтр. Аналогично, разности «выделяют» среди значений межпиксельные всплески и устраняют константную составляющую. То есть, они «отфильтровывают» низкие частоты [2].
Таким образом, преобразование Хаара — это пара фильтров, разделяющих сигнал на низкочастотную и высокочастотную составляющие. Чтобы получить исходный сигнал, нужно просто снова объединить эти составляющие. Пусть есть фотография-портрет. Низкочастотная составляющая несёт в себе информацию об общей форме лица, о плавных перепадах яркости. Высокочастотная — это шум и мелкие детали.
Обычно, когда мы смотрим на портрет, нас больше интересует низкочастотная составляющая, а это значит, что при сжатии часть высокочастотных данных можно отбросить. Тем более, что, она обычно имеет меньшие значения, а значит более компактно кодируется. Степень сжатия можно увеличить, применяя преобразование Хаара многократно. В самом деле, высокочастотная составляющая — это всего лишь половина от всего набора чисел. Но можно применить эту процедуру ещё раз и к низкочастотным данным. После повторного применения высокачастотная информация будет занимать уже 75%.
Были рассмотрены одномерные цепочки чисел, но этот подход хорошо применим и для двумерных данных. Чтобы выполнить двумерное преобразование Хаара (или аналогичное), нужно лишь выполнить его для каждой строки и для каждого столбца. После многократного применения к фотографии замка Лихтенштейн, получим следующий рисунок.

Рис. 7. Многократное применение вейвлет-преобразования
Черные области соответствуют низкой яркости, то есть значениям, близким к нулю. Как показывает практика, если значение достаточно мало, то его можно округлить или вообще обнулить без особого ущерба для декодированного рисунка. Этот процесс называется квантованием. И именно на этом этапе происходит потеря части информации. [3]
Это лишь один из методов вэйвлет-преобразований, причём, не самый лучший. Но даже он позволяет получить хорошее изображение при довольно сильном сжатии. Преобразование Хаара можно улучшить, чтобы оно обнуляло ещё и линейную составляющую. Иными словами, если значения яркости будут увеличивать линейно, то они тоже обнулятся. Эту задачу и более сложные (устранение моментов более высоких порядков) решила Ингрид Добеши — один из создателей теории вэйвлетов. Вэйвлеты Добеши относятся к группе ортогональных вэйвлетов и обладают свойствами, присущими данной группе. Они несимметричны. Вэйвлеты Добеши имеют носители минимального размера для любого заданного числа нулевых моментов p . Ниже представлен график функции вэйвлета «Daubechies».
Интеграл функции: 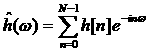
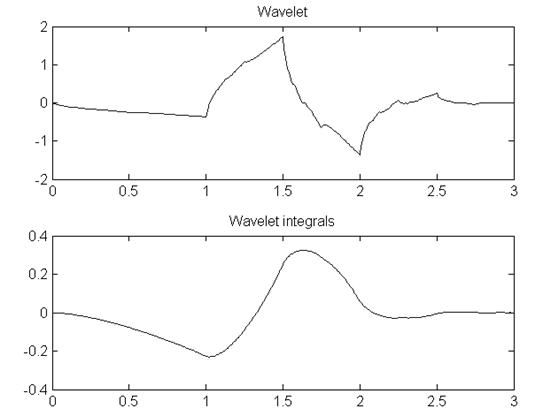
Рис. 8. Вид вэйвлета и его интеграла
Среди профессионального и наиболее современного программного обеспечения, способного решать довольно сложные задачи практического применения вэйвлет и вэйвлет преобразований, можно выделить три основных программных пакета – Mathcad 2001 Professional, Matlab 7, Mathematica 4.1. Эти программные комплексы применимы, как и для самого анализа свойств вэйвлет-функций и вэйвлет преобразований, так и для их использования в задачах обработки цифровых сигналов и изображений. Непосредственно для работы с вэйвлетами используются соответствующие расширения, интегрированные в эти программные пакеты: Wavelet Toolbox (Matlab), Wavelet Extension Pack (Mathcad), Wavelet Explorer (Mathematica). В каждом их них можно протестировать сжатие изображений с естественными, искуственными и другими шумами. Кроме того, в Wavelet Toolbox (Matlab) возможно провести эксперименты с различными методами построения нуль-деревьев вэйвлетов [7].
После проведенных исследований, в которых изучались сжатия изображений с различными шумами при помощи трех вэйвлетов (bior, db, coif) и методов: EZW (Embedded Zerotree Wavelet coder - алгоритмом вложенного нульдерева), STW (Spatial-orientation Tree Wavelet – алгоритм дерева ориентированного в пространстве), можно сказать, что результаты нельзя относить к изображениям с естественными шумами. По результатам наилучшее сжатие изображений достигалось при использовании вэйвлета db и метода сжатия STW. При исследовании изображений с естественными шумами (снег, грязь, туман и т.д.) наилучшие результаты дали вэйвлет db4 в сочетании с методами EZW и STW.
В итоге можно сказать, что использование сжатия изображений (причём, можно применять не только к фото, но и к видео, особенно, если есть много кадров, на которых яркость пикселей изменяется незначительно) с помощью вэйвлетов на порядок лучше известных, но уже устаревших методов. Вэйвлеты могут использоваться в медицине, в космических технологиях (например, фотографии, которые присылает марсоход Curiosity сжимаются именно с помощью вэйвлет-преобразования [5]) или робототехнике. По сути, в любой области, где требуется цифровая обработка изображений и их хранение. Причём, где важна не каждая деталь, а общая картина, только тогда использование вэйвлетов будет максимально оправдано. Недостатком вэйвлет-преобразований, пожалуй, является только их относительная сложность.
ЛИТЕРАТУРА
Г. Штарк, Применение вэйвлетов для цифровой обработки сигналов. – М.: Техносфера, 2007. – 192 с.
К. Чуи, Введение в вэйвлеты. – М.: Мир, 2001. – 416 с., стр.5
Блог Хабрахабр. Вэйвлет-сжатие «на пальцах», 10 февраля 2013. http://habrahabr.ru/post/168517/, стр. 6
Wikipedia, «Сжатие с использованием вэйвлет», http://ru.wikipedia.org/wiki/Сжатие_с_использованием_вэйвлет, стр. 2
Wikipedia, вэйвлет-преобразование ICER, созданное NASA для , http://ru.wikipedia.org/wiki/ICER, стр.10
Воробьев В.И., Грибунин В.Г. “Теория и практика вэйвлет-преобразования.”, ВУС, 1999. С. 1-204., стр. 4
Смоленцев Н. К. “Основы теории вэйвлетов. Вэйвлеты в MATLAB.” - М: ДМК Пресс, 2005. – 304, стр. 7