BC/NW 2014 №1 (24):8.1
ТОПОГРАФИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ИМИТАЦИОННЫХ МОДЕЛЕЙ ДИСКРЕТНО-НЕПРЕРЫВНЫХ ПРОЦЕССОВ НА ПОВЕРХНОСТИ ЗЕМЛИ
Емельянов А.А., Емельянова Н.З.
Типовыми задачами, в которых необходимо использовать точную топографическую информацию, являются: прокладка маршрутов движения техники в новых меняющихся условиях (в т.ч. в оперативной обстановке при возникновении ЧС), определение путей прокладки линий электропередач и монтажа новых подстанций, решения по топологии кабельных информационных сетей, прокладка маршрутов нефте- и газо-трубопроводов, монтаж новых сетей водоснабжения, размежевание территории, анализ обеспечения населения энергией, товарами и услугами. В докладе представлены технологические свойства геоинформационных программных средств системы имитационного моделирования Actor Pilgrim.
ВВЕДЕНИЕ
Существуют родственные с математической точки зрения задачи маршрутизации и размежевания территории, которые традиционно считаются задачами статической оптимизации. Они решаются различными средствами, самым мощным их которых является динамическое программирование.
При полном отсутствии ограничений (например, используется вертолёт, причём пункт старта и пункт финиша – это один пункт, и неважно – какой), как правило, задача имеет единственное решение определения кратчайшего маршрута. Однако при появлении ограничений на пункты, маршруты, допустимые ландшафтные условия, стоимость путей и пропускные способности, количество вариантов становится практически неограниченным сверху, и применение методов статической оптимизации становится проблематичным.
В таком случае можно предложить мощное решение: от методов статической оптимизации перейти к динамической модели адаптивной поисковой системы, обладающей особой памятью, контурами положительной и отрицательной обратных связей по управлению [1]. Однако поиск такая система должна вести в определённых условиях.
1. ТОПОГРАФИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КОМПЬЮТЕРНЫХ РАСЧЁТОВ
В настоящее время существуют следующие источники крупномасштабной топографической информации, пригодной для измерений:
– карты ГШ МО РФ (самые подробные);
– карты ФГУП «Госгисцентр» (ГГЦ-карты);
– карты и космические фотоснимки Google;
– иногда используют системы GPS и ГЛОНАСС.
ГГЦ-карты могут закачиваться, например, в автомобильные GPS-навигаторы или использоваться в устройствах ГЛОНАСС, внедряемых на автомобильном транспорте в связи с решениями руководящих органов. Их применение возможно и в экономических проектах. Но проведение с помощью ГГЦ-карт компьютерных измерений и вычислений невозможно без специальных компьютерных методов и программ, поскольку привязка навигационных систем GPS и ГЛОНАСС к координатам Земли по умолчанию осуществляется по показаниям навигационных спутников Земли. Относительная погрешность такой привязки мала, но абсолютная точность страдает из-за наличия временнóго «дрейфа» точки пересечения поверхности условного эллипсоида Земли «вертикалью» спутника – условной линии, соединяющей спутник с центром эллипсоида; причём у каждого спутника свой дрейф.
Первые два источника используют международные стандарты разграфки и номенклатуры, что обеспечивает очень точную привязку к поверхности Земли каждого электронного (бумажного) листа. Для использования карт ГШ МО РФ требуется разрешение Роскартографии и других ведомств.
Разграфка – это формализованные стандартные правила «раскроя» поверхности Земли на листы масштаба 1:1 000 000 (в 1 см 10 км) и меньших масштабов, например 1:25 000 (в 1 см 250 м): по параллелям с привязкой к экватору и полюсам Земли и по меридианам – с привязкой к Гринвичскому «нулевому» меридиану.
Номенклатура – это стандартный алгоритм идентификации (именования) листов, полученных в результате стандартного раскроя поверхности Земли. По координатам точки однозначно вычисляется идентификатор листа конкретного масштаба, на котором эта точка находится.
2. МОДЕЛЬ АДАПТИВНОЙ ПОИСКОВОЙ СИСТЕМЫ
Система должна обладать следующими свойствами. Память системы предназначена для запоминания информации о последних маршрутах. При выполнении очередной итерации эта память содержит информацию об уже посещённых пунктах. Положительная обратная связь предназначена для «консервирования» удачных маршрутов. Отрицательная обратная связь работает иначе. Если последнее удачное решение, улучшившее маршрут, имеет номер i , а на следующей итерации более удачное решение не получено, то приоритет решения i уменьшается и используется «законсервированный» маршрут, но коэффициент усиления по отрицательной обратной связи увеличивается, и начинаются случайные попытки поиска новых отрезков пути и их продолжений при достижении каждого пункта. Через конечное число итераций приоритет последнего решения станет нулевым, а поиск уже будет постоянным, и так до тех пор, пока либо не будет найдено более удачное решение, либо процесс поиска не будет принудительно остановлен.
В системе есть три регулятора, управляемых ЛПР: коэффициенты усиления в контурах положительной и отрицательной обратных связей и срок хранения в положительном состоянии приоритета последнего удачного решения. Типичным природным аналогом рассмотренной гипотетической системы (но не более чем!) является муравьиная колония [2]. Этот аналог впервые использовал Марко Дориго, Бельгия (более 200 работ за 20 лет по муравьиным и генетическим алгоритмам). Муравей – насекомое, не имеющее развитой центральной нервной системы. Но муравьиная колония коллективно «вполне разумна» с позиций искусственного интеллекта. Память муравьёв основана на феромонах – летучих нано-веществах. Обнаружено более 20 видов феромонов, с помощью которых муравьи ещё и «общаются». В своих алгоритмах М. Дориго использовал свойства феромона пищи.
3. «МУРАВЬИНЫЙ» АЛГОРИТМ ПОИСКА И РАЗМЕЖЕВАНИЯ ТЕРРИТОРИИ
(ФЕРОМОН ОПАСНОСТИ)
Этот авторский алгоритм [1] основан на следующих предпосылках. Допустим, что в пунктах Астарт и Афиниш находятся две муравьиные колонии (условно обозначим эти колонии и муравьёв из колоний как Ant1 и Ant2), которые должны решить следующую задачу: всю территорию нужно поделить на две зоны ответственности, чтобы:
– между зонами можно было демаркировать условную границу;
– в процессе размежевания муравьи из разных колоний держатся дальше друг от друга под воздействием феромона опасности;
– внутри каждой зоны во время итерации строится субоптимальный маршрут;
– прокладка маршрута проходит в виртуальном абсолютном времени;
– только в конце каждой итерации представители разных колоний оказываются ближе всего друг к другу (до этого они стараются держаться подальше друг от друга);
– для простоты полагаем, что гнёзда метят феромоном опасности – как бы «запирают» для последующего освоения колонией, из которой вышел муравей-«землемер»;
– муравей, находящийся в движении к очередному пункту, чтобы включить его в состав своей зоны, не может планировать наперёд посещение другого пункта, так как другой муравей тоже находится в движении и может раньше и спланировать, и занять его, а конфликты запрещены феромоном опасности.
При этом задача коммивояжера может быть сведена к минимаксной игровой задаче двух партнеров, оптимизация решения которой достигается за счет выбора ближайшего пункта с максимальной вероятностью принадлежности к своей зоне ответственности. Если определить множество W, уменьшающееся после каждой итерации на один элемент, как набор нераспределённых пунктов, не принадлежащих ни к одной зоне, то условие выбора можно записать так:
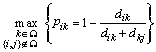 ,
,
где k, i, j – пункты; pik – «мгновенный» вес пункта; dik и dkj – трудоёмкости попадания муравьёв в k.
4. ИМИТАЦИОННАЯ МОДЕЛЬ АДАПТИВНОЙ ПОИСКОВОЙ СИСТЕМЫ
Функциональная схема модели в системе графических обозначений Actor Pilgrim [3] представлена на рис. 1.
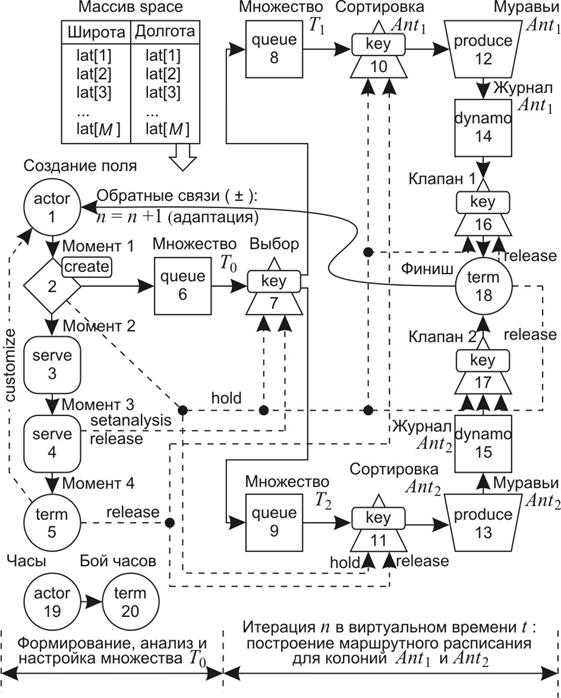 Рис. 1. Имитационная модель работы
адаптивной
Рис. 1. Имитационная модель работы
адаптивной
системы «Муравьиная колония»
Особенностью модели [1] является наличие памяти, состоящей из:
1) «Массива space» – массив пунктов (фактически – это маршрутное расписание с заданным порядком, но неизвестными временами);
2) «Журналов Ant1 и Ant2» – узлов типа dynamo, динамических очередей, выполняющих функции маршрутного журнала муравьёв-«землемеров» Ant1 и Ant2 . При подготовке очередной итерации функция setanalysis разыгрывает минимаксную игровую задачу двух партнеров. Адаптация осуществляется после завершения итерации – переформированием «Массива space», используя «Журналы Ant1 и Ant2». Если отрицательная обратная связь не работает, то поиска не будет.
На рис. 2 представлен вариант решения конкретной задачи, полученный после третьей итерации. При наличии такой модели остаётся только спланировать эксперимент [4], выбрать и ввести в оболочку Actor Pilgrim необходимые карты.
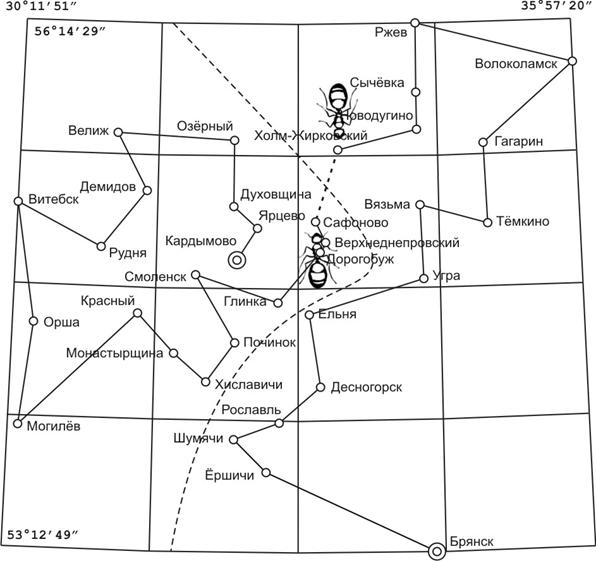
Рис. 2. Решение задачи размежевания: 1) найден оптимальный путь; 2) территория поделена на зоны
5. ПРОГРАММНАЯ ПРИВЯЗКА РАСТРОВОЙ ТОПОГРАФИЧЕСКОЙ ИНФОРМАЦИИ К ГЕОГРАФИЧЕСКИМ КООРДИНАТАМ ЗЕМЛИ В ACTOR PILGRIM
Авторы имели многолетний опыт работы с платформами Environmental Systems Research Institute – ESRI, США (начинали с ArcView, затем ArcInfo и ArcGIS). Имелся и опыт работы и с платформой MapInfo Professional. Принципиальных трудностей стыковки оболочки моделей Actor Pilgrim нет: она программно-предусмотрена. Однако есть две технологические трудности [1].
Первая. В 100% случаях задания на разработку новых Pilgrim-моделей были связаны с территориями, для которых исторически не было крупномасштабной топографической информации ни в одной базе. Возникала необходимость, во-первых, получения её (что организационно непросто), и, во-вторых, поддержки технологической линии ввода этой информации послойно в соответствующую базу. В лучшем случае новая информация – электронный растр, в худшем – крупномасштабные топографические бумажные карты или старые, но точные кальки из специальных хранилищ. Технология, реализованная для ввода ГЕО-информации в оболочку Actor Pilgrim, сократила время подключения моделей для доступа к отсутствующей информации с недели до десятков минут (в пределах часа). Ввод новой информации в базы одной их вышеуказанных платформ проводился, но по факту – уже после проведения модельных экспериментов и принятия на их основе решений.
Вторая. Использование вышеуказанных платформ для индикации в конкретных моделях во время их выполнения потребовало бы, кроме создания самих программных моделей, программировать соответствующие приложения средствами этих платформ (практически для каждой модели – своё приложение).
6. МЕТОДИКА ПРИВЯЗКИ НОВОЙ КАРТЫ ПО ЭТАЛОННЫМ ТОЧКАМ
Рассмотрим растровую карту (электронный лист) – точную карту, соответствующую международным правилам нанесения информации, выполненную в нормальной конической проекции, на которой есть как минимум две точки A1 и A2, координаты которых известны с очень высокой точностью: например, это могут быть точки пересечения основных параллелей и меридианов (рис. 3).
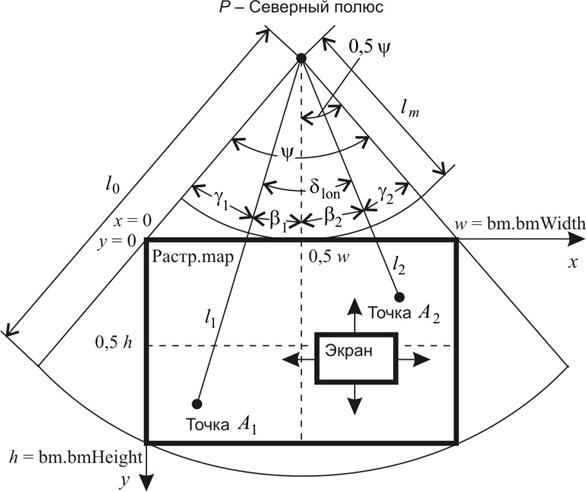
Рис. 3. Схема привязки электронной растровой
карты
На рис. 3 используются обозначения:
а) углы нормальной конической развёртки электронного листа (в радианах): y – угол между меридианами, окаймляющими электронный лист; dlon – угол между меридианами, проходящими через эталонные точки А1 и А2; g1 – угол между западным окаймляющим меридианом и меридианом А1; b1 – угол между меридианом А1 и серединным (вертикальным) меридианом листа; g2 – угол между восточным окаймляющим меридианом и меридианом А2; b2 – угол между меридианом А2 и серединным (вертикальным) меридианом листа;
б) расстояния (внутри компьютера пересчитываются в рабочие единицы-пиксели): h и w – высота и ширина электронного листа; l0 и lm – соответственно, расстояния от Северного полюса до нижней и верхней параллелей, окаймляющих электронный лист; l1 и l2 – соответственно, расстояния от Северного полюса до точек A1 и A2; x и y – рабочие координаты (в расчётах используется развёртка bitmap).
Авторская методика (математическое и программное обеспечение [5]) использует особый математический аппарат – сферическую тригонометрию Феодосия Николаевича Красовского [6]. Основные этапы этой методики перечислены ниже (см. обозначения на рис. 3):
1. Определение угла y между крайними меридианами, используя референц-эллипсоид с радиусами: 6 378 245,000 м – экваториальный; 6 356 863,019 м – полярный.
2. Привязка карты по долготе.
3. Привязка карты по широте.
4. Определение географических координат точек на карте, необходимых для последующих измерений и формирования растровых образов.
Замечание. Математический аппарат, используемый в данной методике, обеспечивает точность расчётов расстояний по поверхности эллипсоида и высот (впадин) от поверхности эллипсоида в пределах 0,001 м, что существенно превышает точность используемых в России крупномасштабных топографических карт (до 1:25 000), карт Google, а также разрешающие возможности экрана компьютера и мыши. Основной источник погрешностей – используемые основы топографической информации.
На рис. 4 показан интерактивный процесс измерений на территории г. Смоленска при использовании крупномасштабной топографической основы в учебном имитационном эксперименте.
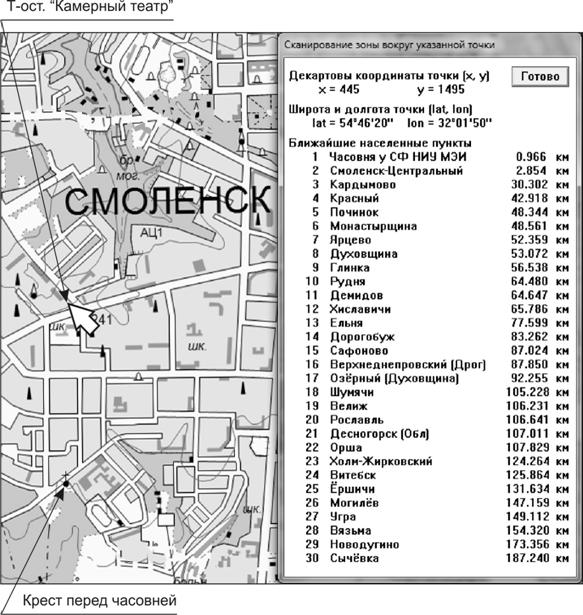
Рис. 4. Измерения расстояний в центре Смоленска (электронный источник: ГГЦ-карта 1:25 000)
Рассмотренные методы использовались при решении конкретных экономических задач, в которых потребовались совместные исследования временной, пространственной и финансовой динамики в Московском регионе. В таких задачах предпочтение отдается специализированному пакету имитационного моделирования Actor Pilgrim [7].
ЗАКЛЮЧЕНИЕ
1. Без точного представления пространства в компьютерной модели в рамках точности топографических карт невозможно обеспечить точность результатов имитационного моделирования экономических и иных процессов в регионе, хотя бы в пределах относительных погрешностей используемых карт. Компьютерное представление региона строится на математической основе, элементами которой на карте являются координатные сетки, масштаб и геометрическая проекция развёртки.
2. Динамический муравьиный алгоритм «размежевания территории» для минимизации маршрутов при наличии существенных ограничений обладает более быстрой сходимостью по сравнению с ранее известными муравьиными алгоритмами. Однако он имеет общий для подобных эвристических алгоритмов недостаток: при достижении конечного варианта маршрута нет возможности доказать, построен ли кратчайший путь.
3. Растровые карты очень нужны, но только для съёма информации на этапе планировании эксперимента, когда на основе топографической информации с помощью программных средств оболочки Actor Pilgrim в модели создаются векторные образы пространства (точки, линии, геометрические фигуры), элементы которых участвуют в модельных расчётах после съёма всей необходимой информации с крупномасштабных растровых карт. Во время выполнения модели растровые карты используются только для индикации (либо не используются).
СПИСОК ЛИТЕРАТУРЫ
1. Емельянов А.А., Емельянова Н.З. Технология работ с топографической информацией в имитационных моделях Actor Pilgrim // Прикладная информатика, № 4 (46), 2013, С. 65-91.
2. Dorigo M., Birattari M., Stützle T. Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique // IEEE Computational Intelligence Magazine, № 1 (4), 2006, pp. 28–39.
3. Емельянов А.А. Концепция и возможности акторно-ориентированной системы имитационного моделирования Actor Pilgrim: Часть I // Прикладная информатика, № 6 (42), 2012, С. 49-66; Часть II // Прикладная информатика, № 1 (43), 2013, С. 41-53.
4. Емельянов А.А. Планирование экстремальных экспериментов с имитационными моделями // Прикладная информатика, № 3 (45), 2013, С. 76-90.
5. Компьютерная имитация экономических процессов / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с.
6. Красовский Ф.Н. Избранные сочинения. Том 1. – М.: Геодезиздат, 1953. – 374 с.
7. Национальное общество имитационного моделирования России – начало пути: Интервью Р.М. Юсупова, члена-корреспондента РАН, директора СПИИ РАН // CAD/CAM/CAE Observer (Latvija, Rīga), № 2 (70), 2012, С. 10-18.