BC/NW 2015 № 1 (26) 8:1

ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ ОПРЕДЕЛЕНИЯ КРАТЧАЙШИХ МАРШРУТОВ

Абросимов Л.И

1 Постановка задачи

Для вычислительных сетей актуальной задачей является выбор кратчайших маршрутов. Успешное решение этой задачи позволяет:

- повысить производительность вычислительной сети,

- повысить эффективность использования ресурсов,

- сократить время реакции вычислительной сети при обслуживании пользователей.

Рассматриваемая задача может быть сформулирована следующим образом. Пусть задана конфигурация S, содержащая множество узлов A, i = , пара которых  и  может быть соединена дугой  Узлы ,  соответствуют устройствам ВС, а дуги  – каналам, соединяющим устройства ВС. Узлы  размешены во взвешенном пространстве М и каждой дуге  соответствует взвешенное расстояние . Соединение каждой пары узлов  и  обеспечивается маршрутом  , который состоит из последовательно соединенных дуг и однозначно определяется номерами узлов, т.е. = {i,…k,   j}.

Между узлом  (источником) и узлом  (целью) могут находиться несколько узлов, тогда маршрут = {i,a,b,c,d,j} – последовательность дуг, образующих связную цепь между узлами i и j.

Например, i-a, a-b, b-c, c-d ,d-j  представляет собой маршрут  ={i →a→b→c→d→j}.

Требуется определить, при каком выборе последовательности {i,…k,   j} узлов в каждом маршруте  обеспечивается минимальная суммарная длина  взвешенных расстояний . дуг  соответствующих конфигурации S и включенных в маршрут  .

Целевая функция сформулированной задачи.

                                                 (1)

где  - начальный узел дуги ;  – конечный узел дуги

Рис. 1 Дуга ,

- булевые неизвестные, удовлетворяющие соотношениям:

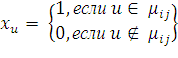                                                  (2)

 - булевые неизвестные, удовлетворяющие соотношениям:

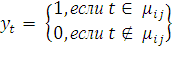                                                        (3)

Ограничения:  (4)

2 Алгоритм определения кратчайших маршрутов

В основу излагаемого вычислительного алгоритма положены идеи алгоритма на графах, который предложил Дейкстра.

В вычислительном алгоритме для поиска оптимального решения используется процедура 1.

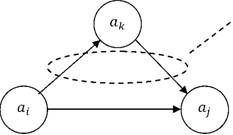
Рассмотрим три узла , , , соединенных дугами ,,  для которых известны взвешенные расстояния , ,  ,  как показано на рис.6.2.

, , k i,  k j , kn.              (5) Рис.2. Процедура поиска оптимального решения

 Пусть необходимо найти кратчайший маршрут  между узлами , . В рассматриваемом случае между узлами ,  может быть два маршрута:

 – прямой, имеющий взвешенное расстояние  =  ;

 – с промежуточным узлом, имеющий взвешенное расстояние;

=  .                                                                        (6)

Для выбора оптимального маршрута применяются следующие правила:

1) если >, то выбирается маршрут ={i,k,j} c промежуточным узлом;

2) если , то выбирается прямой маршрут ={i,j}.

Для вычислительного алгоритма используются следующие формы представления заданных, промежуточных и результирующих данных.

Конфигурация S задается матрицей  , где    = (0,1).

Взвешенные расстояния задаются матрицей = , где дуги, отсутствующе в конфигурации (), имеют .

Результаты расчетов представлены в виде матриц:

= – матрица взвешенных расстояний кратчайших маршрутов  .

= – матрица взвешенных расстояний кратчайших маршрутов , в которой на основании свойства вложенности размещается полный набор всех  кратчайших маршрутов  ().

Для определения  по сформированной матрице  используется пошаговая  процедура 2.

1) Для шага g=1,  (n-2>g1), индекс i заносится в формируемую строку маршрута, т.е i .

2) Проверяется, если значение j ,то переход к пункту 3, если значение  = j ,то переход к пункту 4.

3) Значение  заносится в формируемую строку маршрута, т.е.  , изменяется номер шага g= g+1 и переход к пункту 2.

4) Значение j заносится в формируемую строку маршрута, т.е.  , завершается процедура и выводится список индексов узлов, составляющих маршрут  .

Пример определения по матрице   маршрута :

	1	b	c	a	n
1
b			c
c			c
a			b
n

1) На шаге g=1,  = {a}.

2)  = b,    bc переход к пункту 3.

3) ,  = {a,b},  g=2     переход к пункту 2.

2)  = c,    b=c переход к пункту 4.

4) Результат: = {a,b,c}.

Вычислительный алгоритм определения кратчайших маршрутов, приведенный на рис. 3, включает процедуры 1 и 2 и содержит следующие пункты.

1. Для заданной сети с конфигурацией S=, формируются:  матрица  конфигурации, матрица  взвешенных расстояний и матрица  прямых маршрутов.

Матрица  конфигурации формируется по соотношению:

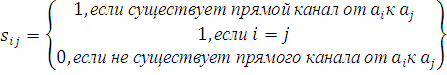   (7)

Матрица  взвешенных расстояний формируется по соотношению:

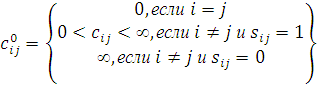                             (8)

Матрица  прямых маршрутов формируется по соотношению:

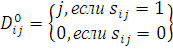                                                        (9)

2. Резервируются для текущих значений матрицы  и , устанавливаются в ноль счетчики индексов начальных (i) и конечных (j) узлов.

3, 4. Увеличиваются значения счетчиков индексов начальных (i) и конечных (j) узлов.

5, 6. Проверяются ограничения    i j , j=n.

7. Устанавливается в ноль счетчик индексов промежуточных (k)  узлов.

8. Увеличивается значение счетчик индексов промежуточных (k)  узлов.

9,10,11. Проверяются ограничения k i,  k j , k=n.

12. В соответствии с процедурой 1 вычисляется текущее значение взвешенных расстояний  маршрута через промежуточный узел и сравнивается с значением прямого маршрута. Если условие выполняется, то переходим к п. 13, если не выполняется – к п.15.    

13, 14. Заносятся значения:   в текущую матрицу  взвешенных расстояний и k – в текущую матрицу  маршрутов.

15, 16,17. Проверяются ограничения k=n, j=n, i=n.

18,19. Текущие значения  и  записываются в результирующие матрицы  и . Используя процедуру 2, получаем кратчайшие маршруты .

Рис. 3 Алгоритм определения кратчайших маршрутов

3 Пример определения кратчайших маршрутов

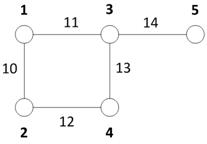
Задана сеть, представленная на рис. 4. Требуется определить кратчайшие маршруты, используя вычислительный алгоритм определения кратчайших маршрутов.

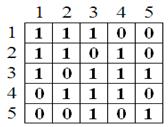
Для формирования матрицы S конфигурации, (см. рис. 5), используется соотношение (6.7).

Рис. 4 Конфигурация заданной сети

S=

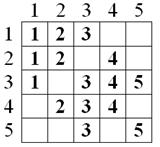
Рис . 5 Матрица S конфигурации

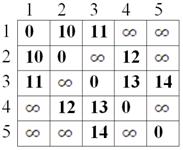
В соответствии с п.1 алгоритма по соотношению (8) формируется матрица  взвешенных расстояний (см. рис. 6), и по соотношению (9) формируется матрица  прямых маршрутов, приведенная на рис.  7.

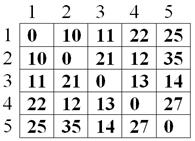
Рис. 6 Матрица

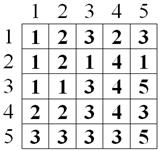
Рис. 7 Матрица

Выполнение п.п. 3 – 11 алгоритма позволяет выбрать номера узлов i, j, k , которые соответствуют ограничениям (4), (5).

i=1, j=2, k=3

По п.12 алгоритма вычисляются по соотношению (6)

=  = 11+ = и   = 10 

Так как  >  , то повторяются п.п. 3 – 11 алгоритма и на одном из шагов выбираются номера узлов i, j, k , которые соответствуют ограничениям (4), (5):  i=1, j=4, k=2.

=  = 10 + 12 = 22 и   =

Так как  < , то переходим к п.13.

По п.13 в матрице   значению  присваивают = 22.

По п.14 в матрице   значению  записывается k = 2.

Последовательное выполнение алгоритма заканчивается, если i =5, j =5, k =5 .

Результат расчета: матрица  записывается в матрицу  (см. рис. 8), матрица  записывается в матрицу  (см. рис. 9) .

Рис. 8 Матрица

=

Рис. 9 Матрица

Для определения кратчайшего маршрута между любыми заданными узлами используется процедура 2.

Например, если  i =2, j =5, , то  = (2,1,3,5).