BC/NW 2015 № 2 (27):12.3

ОПРЕДЕЛЕНИЕ СООБЩЕСТВ В СОЦИАЛЬНОМ ГРАФЕ

Мизинов С.В., Русинов С.Г., Добряков П.С., Нефедов Е.Ю.

Сообщества - это локальные плотно соединенные подграфы в социальной сети (соц. графе). Это утверждение основывается на двух гипотезах: связности и плотности [1].

1) Каждое сообщество представляет связный подграф, на рисунке 1 они сформированы красными и синими вершинами. Если сеть состоит из нескольких компонентов связности, каждое сообщество находится  только в одном из них. На рисунках компонент связности концептуально изображен пунктирным контуром.  Гипотеза также предполагает, что в одной компоненте связности сообщество не может состоять из двух подграфов, которые не имеют связи друг с другом. Следовательно, красные и синие вершины образуют отдельные сообщества.

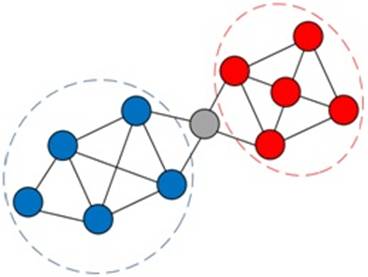
Рис. 1.  Выделение сообществ на основе связности

2) Вершины в сообществе соединены бо́льшим количеством связей друг с другом, чем с вершинами других сообществ и с остальными вершинами сети. Выделенные зеленым вершины удовлетворяют этому ожиданию.

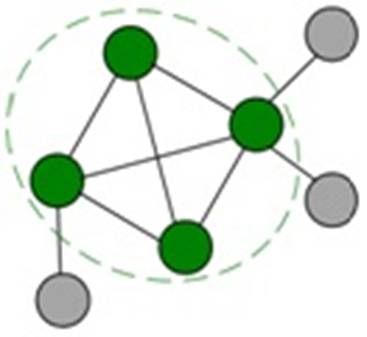
Рис. 2. Выделение сообщества на основе плотности

Хотя этих двух гипотез недостаточно для строгого определения  понятия “сообщество”, с учетом неких допущений большинство  сообществ будет им удовлетворять.

Например, такое предположение о структуре сообществ в графе, согласно которому каждая вершина графа входит только в одно сообщество. Это предположение упрощает обработку данных, но не всегда может быть использовано в случае перекрывающихся сообществ, что часто встречается в реальных данных. Из этого предположения сразу следует, что сообщества полностью покрывают граф. Тогда можно говорить о поиске сообществ в графе как о задаче поиска разбиения множества вершин на подмножества.

Есть другой взгляд на исходную проблему как на задачу кластеризации. Если добавить такую меру как расстояние между вершинами графа, с учетом структурной информации можно решать задачу кластеризации. Далее задачу кластеризации или поиска разбиения можно рассматривать в рамках выделения сообществ в графе.

Один из первых документов о структуре сообществ, опубликованный в 1949 году, определял сообщество как группу лиц, в которой все знают друг друга. В терминах теории графов это означает, что сообщество является полным графом, или кликой.

Клика автоматически удовлетворяет ранее описанным гипотезам связности и плотности: это связный подграф с максимальной плотностью компоновки. Тем не менее, определение сообществ как клик имеет существенный недостаток. В то время как триплеты (клика, состоящая из 3 вершин) часто встречаются в сети, клики с большим числом вершин редки. Следовательно, определение сообщества как полного подграфа сильно ограничивает анализ социальных сетей. Чтобы ослабить ограничение перейдем от полного графа к связному. Связный граф — граф, содержащий ровно одну компоненту связности, между любой парой вершин этого графа существует как минимум один путь.

Рассмотрим сообщество как связный подграф C состоящий из N_c вершин сети G. Внутренней степенью d_i^int вершины i является количество инцидентных ребер, соединяющих ее с вершинами C. Внешней степенью d_i^ext вершины i является количество инцидентных ребер, соединяющих ее с остальными вершинами сети, т.е. вершинами G. В случае d_i^ext=0 все смежные i  вершины принадлежат C, это идеальный случай, чтобы вершину i включить в сообщество C. И наоборот, если d_i^int =0 вершину i следует включить  в другой связный подграф сети G, т.е. в другое сообщество. Эти определения позволяют выделить два вида сообществ:

1) Сильно связное сообщество. Каждая вершина, входящая в сообщество, имеет больше связей внутри сообщества, чем с остальными вершинами сети. В частности, подграф C является сильно связанным сообществом, если для каждой вершины i ∈ C,          (1).

2) Слабо связное сообщество. Суммарная внутренняя степень вершин подграфа больше чем суммарная внешняя. В частности, подграф C является слабо связанным сообществом, если    (2).

Фактически, слабо связное сообщество расширяет сильно связное за счет включения вершин, нарушающих строгое неравенство 1. Каждая клика (полный граф) является сильно связным сообществом, а каждое сильно связанное сообщество является слабо связным. Но не в обратном порядке. Почему этот так, проиллюстрировано на рисунке 3.

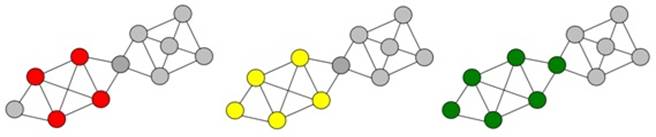
Рис. 3. Виды сообществ. Слева направо: клика, сильно связное сообщество, слабо связное сообщество.

Литература

1. Barabasi Albert-Laszlo.  Network science communities – Cambridge University Press, 2015.  – 498 с.

2 Aaron Clauset, M. E. J. Newman, and Cristopher Moore Finding community structure in very large networks Журнал Phys. Rev. E 70, 066111 –  2004.